试卷题目
1．下列各式：
，
，
，
，
，
(x-y)，
中，分式有( )个．
| a-b |
| 2 |
| x+3 |
| x |
| 5+y |
| π |
| x2 |
| 4 |
| a+b |
| a-b |
| 1 |
| m |
| x2 |
| x |
- A. 2
- B. 3
- C. 4
- D. 5
2．某种感冒病毒的直径是0.00000012米，用科学记数法表示为( )米
- A. 1.2×10-7
- B. 0.12×10-7
- C. 1.2×10-6
- D. 0.12×10-6
3．x=2是方程mx+5=0的解，则函数y=mx+2的图象不经过( )
- A. 第一象限
- B. 第二象限
- C. 第三象限
- D. 第四象限
4．点P(5，-4)关于y轴对称点是( )
- A. (5，4)
- B. (5，-4)
- C. (4，-5)
- D. (-5，-4)
5．已知
-
=2，则
的值为( )
| 1 |
| a |
| 1 |
| b |
| ab |
| a-b |
- A. 0.5
- B. -0.5
- C. 2
- D. -2
6．若点P(1-m，-3)在第四象限，则m的取值范围是( )
- A. m＜1
- B. m＜0
- C. m＞0
- D. m＞1
7．若点(x1，y1)、(x2，y2)和(x3，y3)分别在反比例函数y=-
的图象上，且x1＜x2＜0＜x3，则下列判断中正确的是( )
| 2 |
| x |
- A. y1＜y2＜y3
- B. y3＜y1＜y2
- C. y2＜y3＜y1
- D. y3＜y2＜y1
8．在同一坐标系中，函数y=
和y=kx+3(k≠0)的图象大致是( )
| k |
| x |
- A.
- B.
- C.
- D.
9．若把分式
的x、y同时缩小12倍，则分式的值( )
| x+3y |
| 2x |
- A. 扩大12倍
- B. 缩小12倍
- C. 不变
- D. 缩小6倍
10．百米赛跑中，队员所用的时间y秒与其速度x米/秒之间的函数图象应为( )
- A.
- B.
- C.
- D.
11．如果m是任意实数，则点P(m-3，m+2)一定不在( )
- A. 第一象限
- B. 第二象限
- C. 第三象限
- D. 第四象限
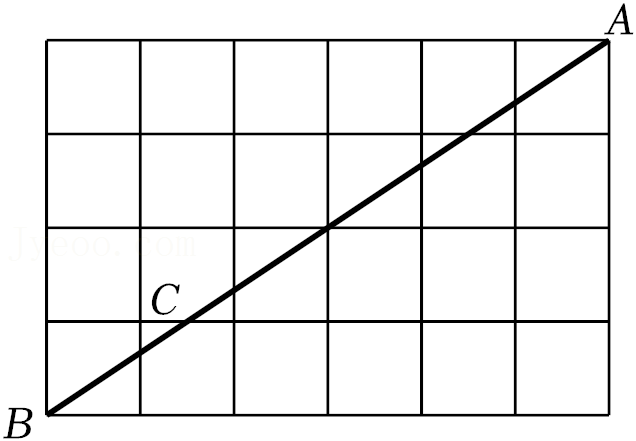
12．如图，已知A点坐标为(5，0)，直线y=x+b(b＞0)与y轴交于点B，连接AB，∠α=75°，则b的值为( )
- A. 3
- B.
5 √33 - C. 4
- D.
5 √34
13．当x= 时，分式
没有意义．
| x2-4 |
| x-2 |
14．在函数y=
中，自变量x的取值范围是 ．
√x+1 |
| 2x-1 |
15．若关于x分式方程
=
有增根，则m= ．
| x-m |
| x-2 |
| 1 |
| x-2 |
16．已知m是整数，且一次函数y=(m+4)x+m+2的图象不过第二象限，则m= ．
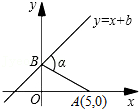
17．A、B两点在双曲线y=
上，分别经过A、B两点向轴作垂线段，已知S阴影=1，则S1+S2= ．
| 5 |
| x |
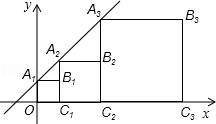
18．正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3…分别在直线y=kx+b(k＞0)和x轴上，已知点B1(1，1)，B2(3，2)，则点B3的坐标是 ，点Bn的坐标是 ．
19．(1)计算：
)-2+(π-3.14)0；
(2)化简：
⋅(
-
)．
√9
-(| 1 |
| 2 |
(2)化简：
| a2b |
| a2-ab |
| a |
| b |
| b |
| a |
20．解分式方程：
(1)
+3=
(2)
-
=1
(1)
| 2-x |
| x-3 |
| 1 |
| 3-x |
| x |
| x-2 |
| 1 |
| x2-4 |
21．先化简，再求值：(1-
)÷
，其中x=(
)-1+1．
| 1 |
| x-1 |
| x2-4 |
| x2+4x+4 |
| 1 |
| 3 |
22．2013年4月20日，四川雅安发生了7.0级地震．在抗震救灾活动中，重庆某厂接到一份订单，要求生产7200顶帐篷支援四川灾区，后来由于情况紧急，接收到上级指示，要求生产总量比原计划增加20%，且必须提前5天完成生产任务，该厂迅速加派人员组织生产，实际每天生产的顶数是原计划每天生产的顶数的2倍，请问该厂实际每天生产多少顶帐篷？
23．如图，A(0，1)，M(3，2)，N(4，4)．动点P从点A出发，沿y轴以每秒1个单位长的速度向上移动，且过点P的直线l：y=-x+b也随之移动，设移动时间为t秒．
(1)当t=3时，求l的解析式；
(2)若点M，N位于l的异侧，确定t的取值范围；
(3)直接写出t为何值时，点M关于l的对称点落在坐标轴上．
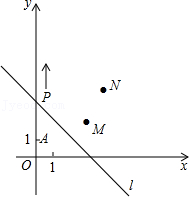
(1)当t=3时，求l的解析式；
(2)若点M，N位于l的异侧，确定t的取值范围；
(3)直接写出t为何值时，点M关于l的对称点落在坐标轴上．
24．由于受金融危机的影响，某店经销的甲型号手机今年的售价比去年每台降价500元．如果卖出相同数量的手机，那么去年销售额为8万元，今年销售额只有6万元．
(1)今年甲型号手机每台售价为多少元？
(2)为了提高利润，该店计划购进乙型号手机销售，已知甲型号手机每台进价为1000元，乙型号手机每台进价为800元，预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台，请问有几种进货方案？
(3)若乙型号手机的售价为1400元，为了促销，公司决定每售出一台乙型号手机，返还顾客现金a元，而甲型号手机仍按今年的售价销售，要使(2)中所有方案获利相同，a应取何值？
(1)今年甲型号手机每台售价为多少元？
(2)为了提高利润，该店计划购进乙型号手机销售，已知甲型号手机每台进价为1000元，乙型号手机每台进价为800元，预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台，请问有几种进货方案？
(3)若乙型号手机的售价为1400元，为了促销，公司决定每售出一台乙型号手机，返还顾客现金a元，而甲型号手机仍按今年的售价销售，要使(2)中所有方案获利相同，a应取何值？
25．如图，一次函数y=kx+b的图象与反比例函数y=
的图象相交于A(-3，2)、B(2，n)两点．
(1)求反比例函数和一次函数的解析式；
(2)求直线AB与x轴的交点C的坐标及△AOB的面积；
(3)根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围．
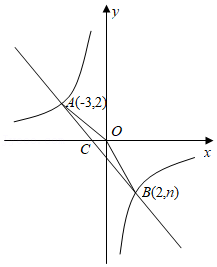
| m |
| x |
(1)求反比例函数和一次函数的解析式；
(2)求直线AB与x轴的交点C的坐标及△AOB的面积；
(3)根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围．
26．在一条直线上依次有A、B、C三个港口，甲、乙两船同时分别从A、B港口出发，沿直线匀速驶向C港，最终达到C港．设甲、乙两船行驶x(h)后，与B港的距离分别为y1、y2(km)，y1、y2与x的函数关系如图所示．
(1)填空：A、C两港口间的距离为 km，a= ；
(2)求图中点P的坐标，并解释该点坐标所表示的实际意义；
(3)若两船的距离不超过10km时能够相互望见，求甲、乙两船可以相互望见时x的取值范围．
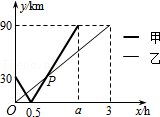
(1)填空：A、C两港口间的距离为 km，a= ；
(2)求图中点P的坐标，并解释该点坐标所表示的实际意义；
(3)若两船的距离不超过10km时能够相互望见，求甲、乙两船可以相互望见时x的取值范围．
