试卷题目
1.下列实数中,有理数是( )
- A. √2
- B. 3√4
- C.
π 2 - D. 3.16
2.若a2=4,b2=9,且ab<0,则a-b的值为( )
- A. -2
- B. ±5
- C. 5
- D. -5
3.下列说法正确的是( )
- A. 有立方根的必有平方根
- B. 算术平方根是它本身的数只有0
- C. 2<√5<3
- D. 数轴上不存在表示√5的点
4.已知x没有平方根,且|x|=64,则x的立方根为( )
- A. 8
- B. -8
- C. ±4
- D. -4
5.下列计算中,正确的是( )
- A. a4+a4=a8
- B. a4•a4=2a4
- C. (a3)4•a2=a14
- D. (2x2y)3÷6x3y2=x3y
6.下列各选项中因式分解正确的是( )
- A. x2-1=(x-1)2
- B. x(x-y)+y(y-x)=(x-y)2
- C. -2y2+4y=-2y(y+2)
- D. x2+xy+x=x(x+y)
7.已知等腰三角形的两边长x,y满足方程组
,则此等腰三角形的周长为( )
| { |
|
- A. 5
- B. 4
- C. 3
- D. 5或4
8.要使多项式(-x2+ax+1)(-6x-b)展开后不含x的二次项,则a与b的关系是( )
- A. ab=-6
- B. ab=6
- C. b=-6a
- D. b=6a
9.如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
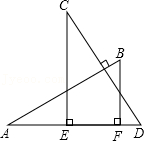

- A. a+c
- B. b+c
- C. a-b+c
- D. a+b-c
10.如图,在△ABC中,∠A=50°,∠B=∠C,点D,E,F分别在边BC,CA,AB上,且满足BF=CD,BD=CE,∠BFD=30°,则∠FDE的度数为( )
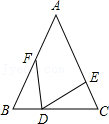

- A. 75°
- B. 80°
- C. 65°
- D. 95°
11.给出四个实数-2,
√3
,0,-1,其中最小的数是 .12.已知25a•52b=5b,4b÷4a=4,则代数式a2+b2值是 .
13.如图,一棵垂直于地面的大树在离地面3米处折断,树的顶端落在离树杆底部4米处,那么这棵树折断之前的高度是 米.
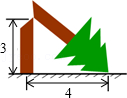

14.如图,在Rt△ACB中,∠C=90°,BE平分∠CBA交AC于点E,过E作ED⊥AB于D点,当∠A= 时,ED恰为AB的中垂线.
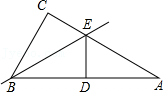

15.甲乙两人完成因式分解x2+ax+b时,甲看错了a的值,分解的结果是(x+6)(x-2),乙看错了b的值,分解的结果为(x-8)(x+4),那么x2+ax+b分解因式正确的结果为 .
16.计算:
(1)-(-1)2018-|2-
(2)(-3ab2)3÷a2b3×(-2ab3c).
(1)-(-1)2018-|2-
√3
|+√81
+3√-27
;(2)(-3ab2)3÷a2b3×(-2ab3c).
17.分解因式:
(1)3x-27x3y2;
(2)3ax2-6axy+3ay2.
(1)3x-27x3y2;
(2)3ax2-6axy+3ay2.
18.先化简,再求值.
当
当
√x-2
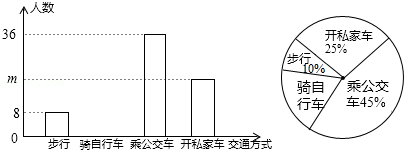
+(y+1)2=0时,求[(3x+2y)(3x-2y)+(2y+x)(2y-3x)]÷4x的值.19.“低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门随机调查了某单位员工上下班的交通方式,绘制了如下统计图,根据统计图,完成下列问题:
(1)调查的总人数为 ;
(2)补全条形统计图;
(3)该单位共有2000人,为了积极践行“低碳生活,绿色出行”这种生活方式,调查后开私家车的人上下班全部改为骑自行车,则现在骑自行车的人数约为多少人?
(1)调查的总人数为 ;
(2)补全条形统计图;
(3)该单位共有2000人,为了积极践行“低碳生活,绿色出行”这种生活方式,调查后开私家车的人上下班全部改为骑自行车,则现在骑自行车的人数约为多少人?

20.小明想测量学校旗杆的高度,他采用如下的方法:先将旗杆上的绳子接长一些,让它垂到地面还多1米,然后将绳子下端拉直,使它刚好接触地面,测得绳下端离旗杆底部5米,你能帮它计算一下旗杆的高度.

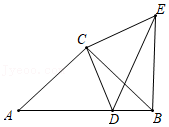
21.如图,△ABC和△CDE均为等腰三角形,AC=BC,CD=CE,∠ACB=∠DCE,点D在线段AB上(与A,B不重合),连接BE.
(1)证明:△ACD≌△BCE.
(2)若BD=2,BE=5,求AB的长.
(1)证明:△ACD≌△BCE.
(2)若BD=2,BE=5,求AB的长.

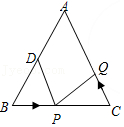
22.如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以3cm/s的速度由B点向C点运动(点P不与点C重合),同时点Q在线段CA上由C点向A点运动.
(1)若点Q的运动速度与点P的运动速度相等,当运动时间是1s时,△BPD与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当△BPD与△CQP全等时,点P,点Q的运动时间是多少?
(1)若点Q的运动速度与点P的运动速度相等,当运动时间是1s时,△BPD与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当△BPD与△CQP全等时,点P,点Q的运动时间是多少?

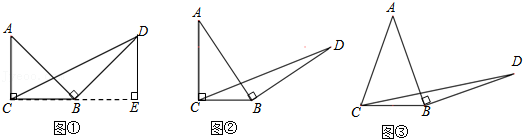
23.问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连接CD.过点D作△BCD的BC边上的高DE,
易证△ABC≌△BDE,从而得到△BCD的面积为
a2.
(1)初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连接CD.用含a的代数式表示△BCD的面积,并说明理由.
(2)简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连接CD.直接写出△BCD的面积.(用含a的代数式表示)
易证△ABC≌△BDE,从而得到△BCD的面积为
| 1 |
| 2 |
(1)初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连接CD.用含a的代数式表示△BCD的面积,并说明理由.
(2)简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连接CD.直接写出△BCD的面积.(用含a的代数式表示)






