试卷题目
1.第24届冬季奥林匹克运动会将于2025年2月4日至2月20日在中国北京市和张家口市联合举办.以下是参选的冬奥会会徽设计的部分图形,其中是轴对称图形的是( )
- A.

- B.

- C.

- D.

2.下列计算正确的是( )
- A. a3-a2=a
- B. (a2)3=a5
- C. a6÷a2=a3
- D. a2•a3=a5
3.下列等式中,从左到右的变形是因式分解的是( )
- A. m(a+b)=ma+mb
- B. x2+3x+2=(x+1)(x+2)
- C. x2+xy-3=x(x+y)-3
- D. 2x2+2x=2x2(1+)
1 x
4.如果(2x+m)与(x+3)的乘积中不含x的一次项,那么m的值为( )
- A. -6
- B. -3
- C. 0
- D. 1
5.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
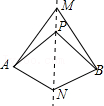

- A. AM=BM
- B. AP=BN
- C. ∠MAP=∠MBP
- D. ∠ANM=∠BNM
6.要使16x2-bx+1成为完全平方式,那么常数b的值是( )
- A. 4
- B. -8
- C. ±4
- D. ±8
7.如图,△ABC中,∠A=40°,AB的垂直平分线分别交AB,AC于点D,E,连接BE,则∠BEC的大小为( )
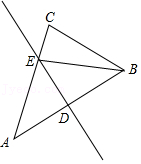

- A. 40°
- B. 50°
- C. 80°
- D. 100°
8.如图,AD是等边△ABC的一条中线,若在边AC上取一点E,使得AE=AD,则∠EDC的度数为( )
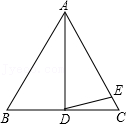

- A. 30°
- B. 20°
- C. 25°
- D. 15°
9.平面直角坐标系中,已知A(2,0),B(0,2)若在坐标轴上取C点,使△ABC为等腰三角形,则满足条件的点C的个数是( )
- A. 4
- B. 6
- C. 7
- D. 8
10.如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
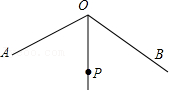

- A. 2个
- B. 3个
- C. 4个
- D. 无数个
11.当 x≠4时,(x-4)0等于 .
12.若等腰三角形中有一个角等于40°,则这个等腰三角形的顶角的度数为 .
13.已知xm=6,xn=3,则x2m-n的值为 .
14.若a2+b2=19,ab=5,则a-b= .
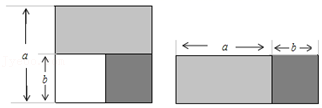
15.如图,从边长为a的大正方形中去掉一个边长为b的小正方形,然后将剩余部分剪后拼成一个长方形,这个操作过程能验证的等式是 .

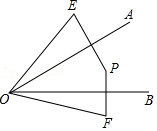
16.如图,点P为∠AOB内任一点,E,F分别为点P关于OA,OB的对称点.若∠AOB=30°,则∠E+∠F= °.

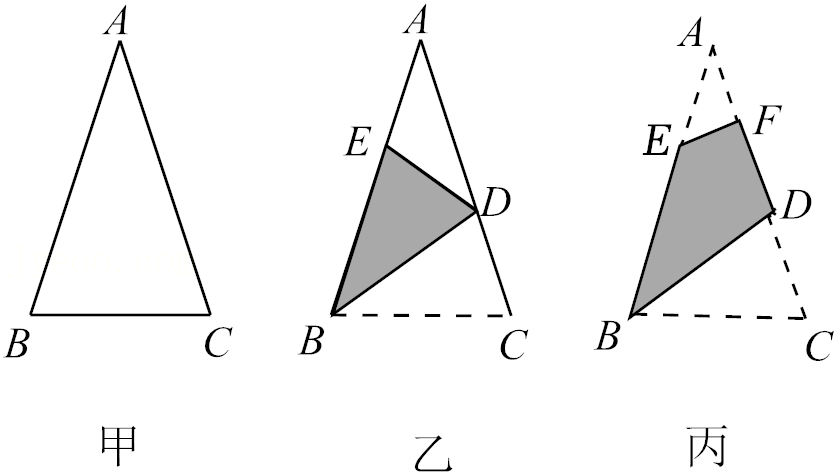
17.已知一张三角形纸片ABC(如图甲),其中∠ABC=∠C.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠ABC的大小为 °.

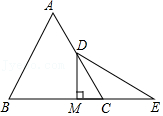
18.如图,在等边△ABC中,D为AC边的中点,E为BC边的延长线上一点,CE=CD,DM⊥BC于点M.下列结论正确的有 .(把所有正确的序号写在横线上)
①DM=
DE
②BM=EM
③2CD=3DM
④BM=3CM
①DM=
| 1 |
| 2 |
②BM=EM
③2CD=3DM
④BM=3CM

19.因式分解;
(1)ax2+2a2x+a3;
(2)(a-b)(x-y)-(b-a)(x+y).
(1)ax2+2a2x+a3;
(2)(a-b)(x-y)-(b-a)(x+y).
20.计解:59
×60
.
| 4 |
| 5 |
| 1 |
| 5 |
21.计算:[7m•m4-(-3m2)2]÷2m2.
22.已知4a2+2b2-1=0,求代数式(2a+b)2-b(4a-b)+2的值.
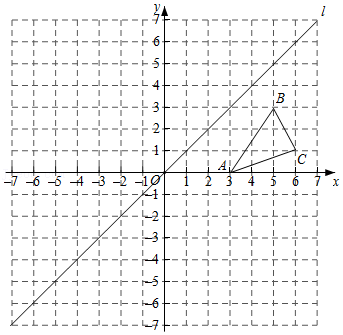
23.如图,在平面直角坐标系xOy中,直线l是第一、三象限的角平分线.已知△ABC的三个顶点坐标分别为A(3,0),B(5,3),C(6,1).
(1)若△ABC与△A'B'C'关于y轴对称,画出△A′B′C′;
(2)若直线l上存在点P,使AP+BP最小,则点P的坐标为 ,AP+BP的最小值为 .
(1)若△ABC与△A'B'C'关于y轴对称,画出△A′B′C′;
(2)若直线l上存在点P,使AP+BP最小,则点P的坐标为 ,AP+BP的最小值为 .

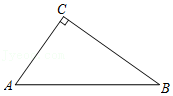
24.如图,在Rt△ABC中,∠C=90°,AC<BC.
(1)画图:
①作AB的垂直平分线,分别与AB交于点D,与BC交于点E;(要求尺规作图,保留作图痕迹)
②连接AE;
③过点B作BF垂直AE,垂足为F.
(2)求证:AC=BF.
(1)画图:
①作AB的垂直平分线,分别与AB交于点D,与BC交于点E;(要求尺规作图,保留作图痕迹)
②连接AE;
③过点B作BF垂直AE,垂足为F.
(2)求证:AC=BF.

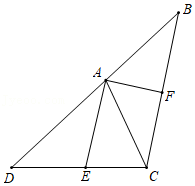
25.如图,AE是△ACD的角平分线,B在DA延长线上,AE∥BC,F为BC中点,判断AE与AF的位置关系并证明.

26.老师在黑板上写出了一道思考题:已知a+b=2,求a2+b2的最小值.
(1)爱思考的小明同学想到了一种方法:先用b表示a,a=2-b;
再把a=2-b代入a2+b2;a2+b2= +b2;
再进行配方得到:a2+b2=2(b- )2+ ;
根据完全平方式的非负性,就得到了a2+b2的最小值是 .
(2)请你根据小明的方法,当x+y=10时,求x2+y2的最小值.
(1)爱思考的小明同学想到了一种方法:先用b表示a,a=2-b;
再把a=2-b代入a2+b2;a2+b2= +b2;
再进行配方得到:a2+b2=2(b- )2+ ;
根据完全平方式的非负性,就得到了a2+b2的最小值是 .
(2)请你根据小明的方法,当x+y=10时,求x2+y2的最小值.
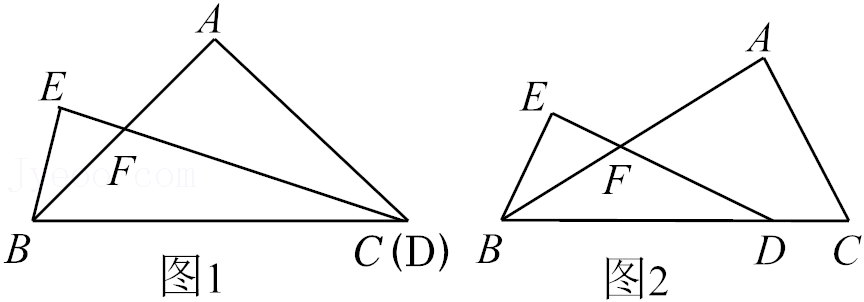
27.在△ABC中,AB=AC,∠A=90°,点D在线段BC上,∠EDB=
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
(1)当C,D两点重合时(如图1)
直接写出∠EBF= °;
直接写出线段BE与FD之间的数量关系 ;
(2)当C,D不重合时(如图2),写出线段BE与FD的数量关系,并证明.
| 1 |
| 2 |
(1)当C,D两点重合时(如图1)
直接写出∠EBF= °;
直接写出线段BE与FD之间的数量关系 ;
(2)当C,D不重合时(如图2),写出线段BE与FD的数量关系,并证明.

28.如图,在平面直角坐标系xOy中,经过点M(0,m),且平行于x轴的直线记作直线y=m.我们给出如下定义:点P(x,y)先关于x轴对称得到点P1,再将点P1关于直线y=m对称得到点P',则称点P'称为点P关于x轴和直线y=m的二次反射点.
(1)点A(5,3)关于x轴和直线y=1的二次反射点A'的坐标是 ;
(2)点B(2,-1)关于x轴和直线y=m的二次反射点B'的坐标是(2,-5),m= ;
(3)若点C的坐标是(0,
m),其中m>0,点C关于x轴和直线y=m的二次反射点是C',求线段CC'的长(用含m的式子表示);
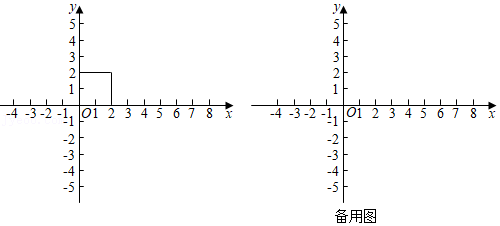
(4)如图,正方形的四个顶点坐标分别为(0,0)、(2,0)、(2,2)、(0,2),若点P(1,4),Q(1,5)关于x轴和直线y=m的二次反射点分别为P',Q',且线段P'Q'与正方形的边没有公共点,直接写出m的取值范围.
(1)点A(5,3)关于x轴和直线y=1的二次反射点A'的坐标是 ;
(2)点B(2,-1)关于x轴和直线y=m的二次反射点B'的坐标是(2,-5),m= ;
(3)若点C的坐标是(0,
| 1 |
| 2 |
(4)如图,正方形的四个顶点坐标分别为(0,0)、(2,0)、(2,2)、(0,2),若点P(1,4),Q(1,5)关于x轴和直线y=m的二次反射点分别为P',Q',且线段P'Q'与正方形的边没有公共点,直接写出m的取值范围.






