试卷题目
1.以下列各组数为边长,能构成直角三角形的是( )
- A. 4、5、6
- B. 1、2、3
- C. 1、2、√5
- D. 1、3、5
2.下列各式中,不正确的是( )
- A. √(-2)2=-2
- B. (√2)2=2
- C. -√(-2)2=-2
- D. ±√(-2)2=±2
3.平行四边形的一边长为6cm,周长为28cm,则这条边的邻边长是( )
- A. 22cm
- B. 16cm
- C. 11cm
- D. 8cm
4.下列二次根式中,与
√3
能合并的是( )- A. √24
- B. √32
- C. √54
- D. √
3 4
5.在▱ABCD中,∠A+∠C=160°,则∠B的度数为( )
- A. 60°
- B. 80°
- C. 100°
- D. 120°
6.如图,某公园的一块草坪旁边有一条直角小路,公园管理处为了方便群众,沿AC修了一条近路,已知AB=40米,BC=30米,则走这条近路AC可以少走( )米路.


- A. 20
- B. 30
- C. 40
- D. 50
7.如图,AB∥CD,AD∥BC,AD=5,BE=8,△DCE的面积为6,则四边形ABCD的面积为( )
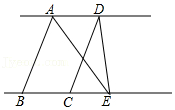

- A. 32
- B. 20
- C. 12
- D. 6
8.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
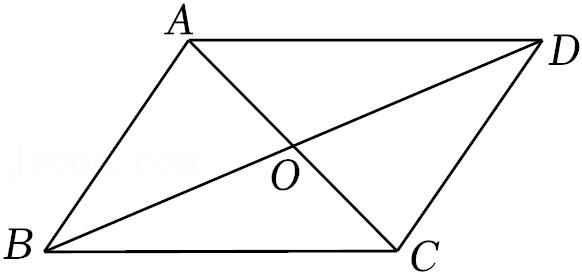

- A. AB∥CD,∠DAC=∠BCA
- B. AB=CD,∠ABO=∠CDO
- C. AC=2AO,BD=2BO
- D. AO=BO,CO=DO
9.如图,由两个直角三角形和三个大正方形组成的图形,其中阴影部分面积是( )
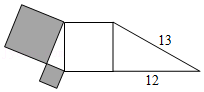

- A. 16
- B. 25
- C. 144
- D. 169
10.如图,△ABC中,AB=AC=4,AE⊥AC,DE垂直平分AB于点D,则EC的长为( )
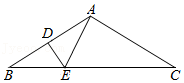

- A.
7 √32 - B.
4 √33 - C.
8 √33 - D. 3√3
11.若
√x-1
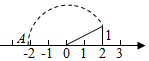
在实数范围内有意义,则x的取值范围是 .12.如图,在数轴上点A表示的实数是 .

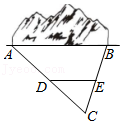
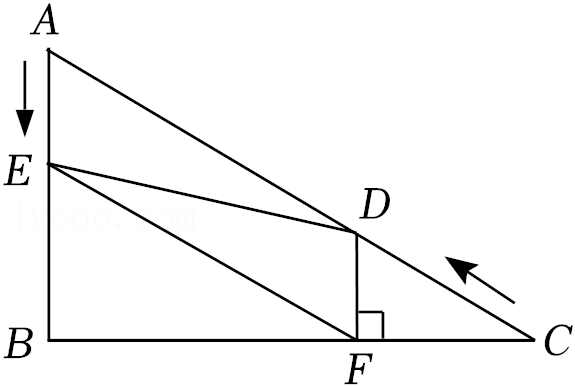
13.某地需要开辟一条隧道,隧道AB的长度无法直接测量,如图所示,在地面上取一点C,使C到A、B两点均可直接到达,测量找到AC和BC的中点D、E,测得DE的长为1100m,则隧道AB的长度为 m.

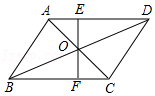
14.已知:在▱ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则▱ABCD的面积是 .

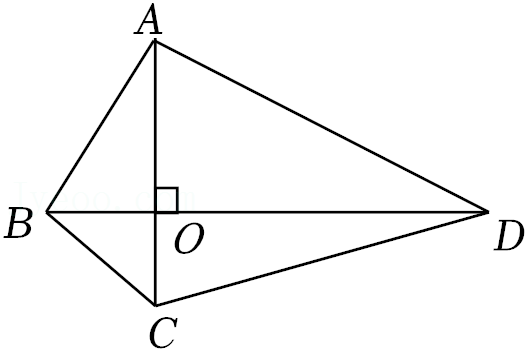
15.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示“垂美”四边形ABCD,对角线AC,BD交于点O,若AB=6,CD=10,则AD2+BC2= .

16.如图在平面直角坐标系中,O为坐标原点,A(1,3),B(2,1),直角坐标系中存在点C,使得点O,A,B,C四点构成平行四边形,则C点坐标为 .
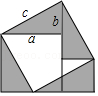
17.“赵爽弦图”巧妙地利用“出入相补”的方法证明了勾股定理.小明受此启发,探究后发现,若将4个直角边长分别为a、b,斜边长为c的直角三角形拼成如图所示的五边形,用等积法也可以证明勾股定理,则小明用两种方法表示五边形的面积分别是(用含有a、b、c的式子表示) , .

18.如图,在▱ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF交于H,BF,AD的延长线交于G,给出下列结论:①DB=
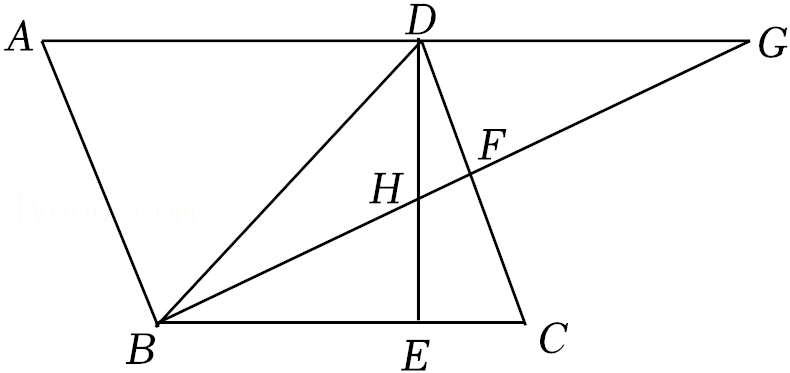
√2
BE;②∠A=∠BHE;③AB=BH;④若BG平分∠DBC,则BE=(√2
+1)EC;其中正确的结论有 .(填序号)
19.计算:
(1)
(2)(
(1)
√12
-√27
+√8
÷√2
;(2)(
√8
+√3
)×√6
-4√
| 1 |
| 2 |
20.计算:
√25
+(π-3)0+|1-√2
|.21.如图,▱ABCD的对角线AC,BD交于点O,E、F分别是OA、OC的中点.
求证:BE=DF.
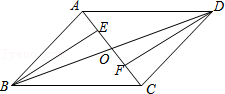
求证:BE=DF.

22.已知x=
√3
+1,求x2-2x+1的值.23.如图,已知平行四边形ABCD的一个内角∠B及其两边长BA,BC.
(1)用尺规补全平行四边形ABCD,请保留作图痕迹并说明你的作图依据;
(2)点E是BC边上任意一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE,简要说明你的作图过程.
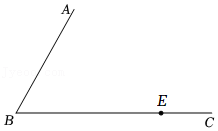
(1)用尺规补全平行四边形ABCD,请保留作图痕迹并说明你的作图依据;
(2)点E是BC边上任意一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE,简要说明你的作图过程.

24.如图,每个小正方形的边长为1,A,B,C,D均为格点.
(1)四边形ABCD的面积为 ,
四边形ABCD的周长为 ;
(2)∠BCD是直角吗?说明理由.
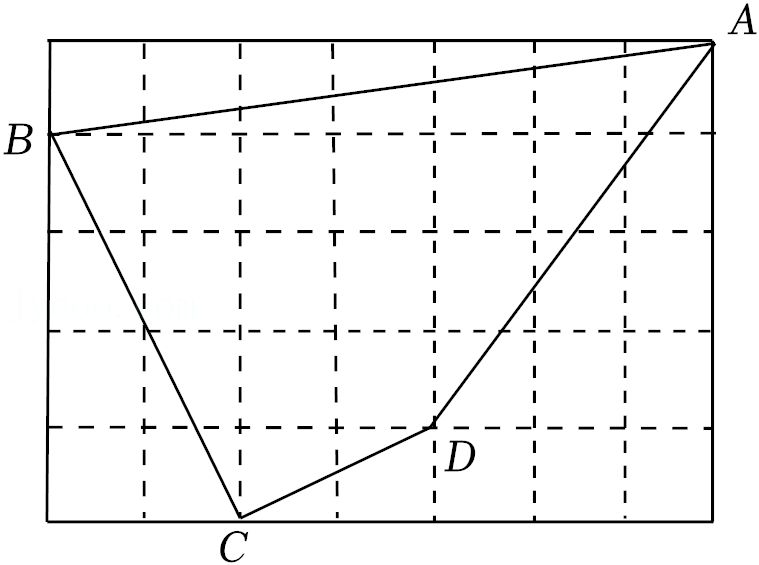
(1)四边形ABCD的面积为 ,
四边形ABCD的周长为 ;
(2)∠BCD是直角吗?说明理由.

25.如图,在△ABC中,∠A=90°,BC=5,AC=3,现将它折叠,使点B与C重合,求折痕DE的长.
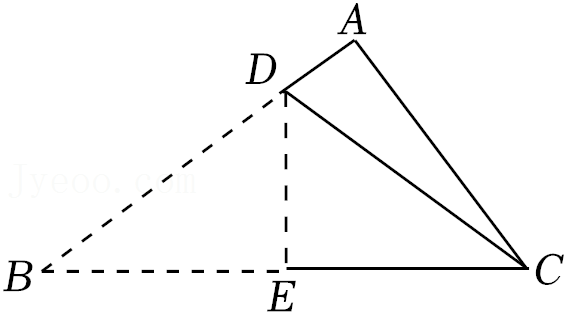

26.如图,在Rt△ABC中,∠B=90°,BC=5
(1)求AB,AC的长;
(2)求证:AE=DF;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
√3
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE,EF.(1)求AB,AC的长;
(2)求证:AE=DF;
(3)当t为何值时,△DEF为直角三角形?请说明理由.

27.数学教育家波利亚曾说:“对一个数学问题,改变它的形式,变换它的结构,直到发现有价值的东西,这是数学解题的一个重要原则”.
材料一:平方运算和开平方运算是互逆运算.如a2±2ab+b2=(a±b)2,那么
材料二:在直角坐标系xOy中,对于点P(x,y)和Q(x,y')给出如下定义:
若y′=
,则称点Q为点P的“横负纵变点”.例:点(3,2)的“横负纵变点”为(3,2),点(-2,5)的“横负纵变点”为(-2,-5).
请选择合适的材料解决下面的问题:
(1)点(
点(-3
(2)化简:
(3)已知a为常数(1≤a≤2),点M(-
(
材料一:平方运算和开平方运算是互逆运算.如a2±2ab+b2=(a±b)2,那么
√a2±2ab+b2
=|a±b|.如何将双重二次根式√5±2
化简?我们可以把5±2√6
√6
转化为(√3
)2±2√6
+(√2
)2=(√3
±√2
)2完全平方的形式,因此双重二次根式√5±2
=√6
√(
=√3
±√2
)2√3
±√2
得以化简.材料二:在直角坐标系xOy中,对于点P(x,y)和Q(x,y')给出如下定义:
若y′=
| { |
|
请选择合适的材料解决下面的问题:
(1)点(
√2
,-√3
)的“横负纵变点”为 ,点(-3
√3
,-2)的“横负纵变点”为 ;(2)化简:
√8+2
= ;√15
(3)已知a为常数(1≤a≤2),点M(-
√2
,m)且m=| 2 |
√2 |
√a+2
+√a-1
√a-2
),点M'是点M的“横负纵变点”,则点M'的坐标是 .√a-1
28.如图1,点A,点B的坐标分别(a,0),(0,b),且b=
(1)直接写出a= ,b= ,点C的坐标为 ;
(2)如图2,作CD⊥x轴于点D,点M是BD的中点,点N在△OBD内部,ON⊥DN,求证:
(3)如图3,点P是第二象限内的一个动点,若∠OPB=90°,求线段CP的最大值.
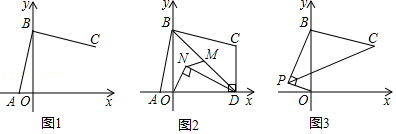
√a+1
+√-1-a
+4,将线段BA绕点B逆时针旋转90°得到线段BC.(1)直接写出a= ,b= ,点C的坐标为 ;
(2)如图2,作CD⊥x轴于点D,点M是BD的中点,点N在△OBD内部,ON⊥DN,求证:
√2
MN+ON=DN.(3)如图3,点P是第二象限内的一个动点,若∠OPB=90°,求线段CP的最大值.





