试卷题目
1.若代数式
有意义,则实数x的取值范围是( )
√x+1 |
| 2 |
- A. x≥-1
- B. x≥-1且x≠0
- C. x>-1
- D. x>-1且x≠0
2.下列二次根式中,最简二次根式是( )
- A. √5
- B. √4
- C. √12
- D. √
1 2
3.如图,数轴上点A对应的数是0,点B对应的数是1,BC⊥AB,垂足为B,且BC=2,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
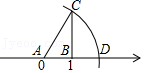

- A. 2.2
- B. √2
- C. √3
- D. √5
4.如图,若D、E、F分别是△ABC三边中点,EF=6cm,DE=4cm,DF=5cm,则△ABC的周长为( )
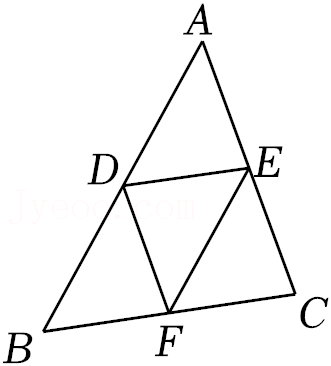

- A. 15cm
- B. 18cm
- C. 30cm
- D. 36cm
5.若下列左边的式子有意义,则运算正确的是( )
- A. √a2=a
- B. √ab=√a⋅√b
- C. (√a)2=a
- D. √=
b a √b√a
6.已知n为正整数,且
√20n
是整数,则n的取值不可能是( )- A. 20
- B. 5
- C. 2
- D. 45
7.满足下列条件时,△ABC不是直角三角形的是( )
- A. AB=√41,BC=4,AC=5
- B. AB:BC:AC=3:4:5
- C. ∠A:∠B:∠C=3:4:5
- D. ∠A=∠B=
1 2 ∠C1 3
8.如图,在平行四边形ABCD中,∠A+∠C=160°,则∠B的度数是( )
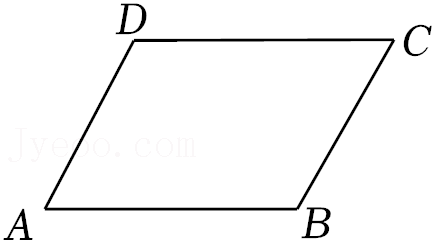

- A. 130°
- B. 120°
- C. 100°
- D. 90°
9.如图,在△ABC中,点E,D,F分别在边AB,BC,CA上,且DE∥CA,DF∥AB.下列四个判断中,不正确的是( )
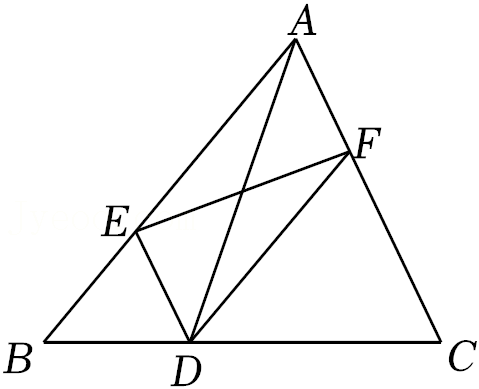

- A. 四边形AEDF是平行四边形
- B. 如果AD=EF,则四边形AEDF是矩形
- C. 若AD⊥EF,则四边形AEDF是菱形
- D. 若AD⊥BC且AB=AC,则四边形AEDF是正方形
10.如图,将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长度是为hcm,则h的取值范围是( )
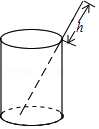

- A. 5≤h≤12
- B. 12≤h≤19
- C. 11≤h≤12
- D. 12≤h≤13
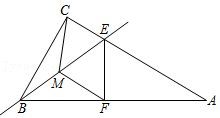
11.如图,在Rt△ABC中,∠ACB=90°,点E是AC边上的动点(点E与点C、A不重合),设点M为线段BE的中点,过点E作EF⊥AB,垂足为点F,连接MC、MF.若∠CBA=50°,则在点E运动过程中∠CMF的大小为( )

- A. 80°
- B. 100°
- C. 130°
- D. 发生变化,无法确定
12.已知直角三角形的斜边长为5cm,周长为12cm,则这个三角形的面积( )
- A. 12cm2
- B. 3cm2
- C. 8cm2
- D. 6cm2
13.化简:
√(3-π)2
= .14.若实数a、b满足|a+2|+
= .
√b-4
=0,则| a2 |
| b |
15.已知菱形的两条对角线长为8cm和6cm,那么这个菱形的面积是 .
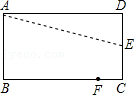
16.如图,折叠矩形ABCD的一边AD,点D落在BC边上的点F处,AE是折痕,已知AB=8cm,BC=10cm.则CE= cm.

17.如图,在正方形ABCD中,点E,F分别在AD,CD上,且AE=DF=2,BE与AF相交于点O,P是BF的中点,连接OP,若AB=5,则OP的长为 .


18.我们把联结四边形对边中点的线段称为“中对线”.凸四边形ABCD的对角线AC=BD=12,且这两条对角线的夹角为60°,那么该四边形较长的“中对线”的长度为 .
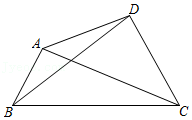

19.计算题:
(1)(3
(2)(2+
(1)(3
√12
-2√
+| 1 |
| 3 |
√48
)÷2√3
;(2)(2+
√3
)(2-√3
)(1+√2
)2.20.如图,一块草坪的形状为四边形ABCD,其中∠B=90°,AB=3cm,BC=4cm,CD=12cm,AD=13cm,求这块草坪的面积.


21.在解决问题:“已知a=
,求3a2-6a-1的值”.
∵a=
=
=
∴a-1=
∴(a-1)2=2,
∴a2-2a=1,
∴3a2-6a=3,
∴3a2-6a-1=2.
请你根据小明的解答过程,解决下列问题:
(1)化简:
= .
(2)若a=
,求2a2-12a-1的值.
| 1 |
√2 -1 |
∵a=
| 1 |
√2 -1 |
√2 +1 |
| ( √2 -1)(√2 +1) |
√2
+1,∴a-1=
√2
.∴(a-1)2=2,
∴a2-2a=1,
∴3a2-6a=3,
∴3a2-6a-1=2.
请你根据小明的解答过程,解决下列问题:
(1)化简:
| 2 |
√5 -2 |
(2)若a=
| 1 |
| 3+2 √2 |
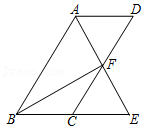
22.如图,在四边形ABCD中,AB∥CD,∠BAD的平分线AE交CD于点F,交BC的延长线于点E,且AB=BE.
(1)求证:四边形ABCD是平行四边形;
(2)连接BF,若BF⊥AE,∠E=60°,AB=6,求四边形ABCD的面积.
(1)求证:四边形ABCD是平行四边形;
(2)连接BF,若BF⊥AE,∠E=60°,AB=6,求四边形ABCD的面积.

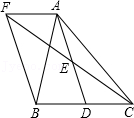
23.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.

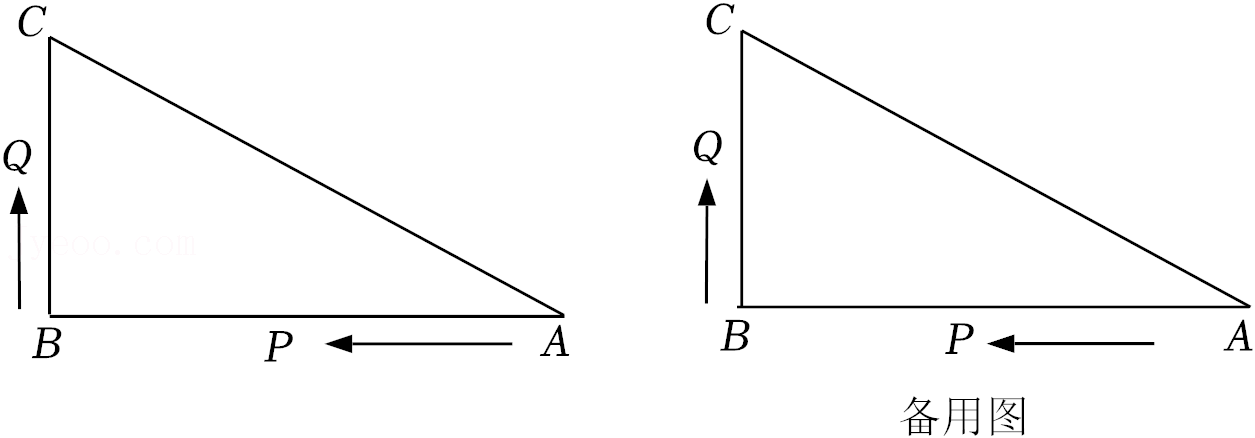
24.如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,同时停止.
(1)P、Q出发4秒后,求PQ的长;
(2)当点Q在边CA上运动时,出发几秒钟后,△CQB能形成直角三角形?
(1)P、Q出发4秒后,求PQ的长;
(2)当点Q在边CA上运动时,出发几秒钟后,△CQB能形成直角三角形?

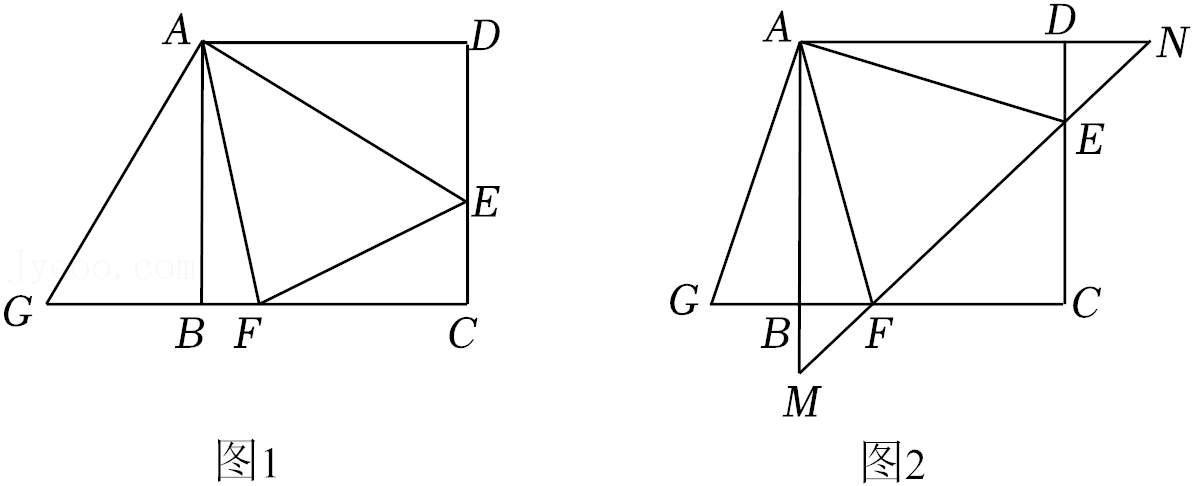
25.在正方形ABCD中,E是CD边上任意一点,连接AE,点F在BC上,∠EAF=45°,连接EF.
(1)以A为圆心,AE为半径作圆,交CB的延长线于点G,连接AG(如图1).求证:BF+DE=EF;
(2)点E在DC边上移动,当EC=CF时,直线EF与AB、AD的延长线分别交于点M、N(如图2),直接写出EF、MF、NE的数量关系: .
(1)以A为圆心,AE为半径作圆,交CB的延长线于点G,连接AG(如图1).求证:BF+DE=EF;
(2)点E在DC边上移动,当EC=CF时,直线EF与AB、AD的延长线分别交于点M、N(如图2),直接写出EF、MF、NE的数量关系: .






