试卷题目
1.现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )
- A.

- B.

- C.

- D.

2.下列计算正确的是( )
- A. b3•b3=2b3
- B. (a5)2=a7
- C. (-2a)2=4a2
- D. (ab)5÷(ab)2=ab3
3.在下列给出的四组条件中,能判定△ABC≌△DEF的是( )
- A. AB=DE,BC=EF,∠A=∠D
- B. ∠A=∠D,∠C=∠F,AC=EF
- C. ∠A=∠D,∠B=∠E,∠C=∠F
- D. AB=DE,BC=EF,△ABC的周长等于△DEF的周长
4.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC,DE⊥AC于点E,则下列结论不正确的是( )
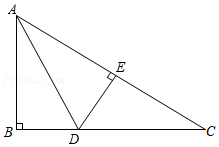

- A. DE=DB
- B. AE=AB
- C. ∠ADE=∠ADB
- D. ED+BD=BC
5.如图,CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE、CD相交于点O.∠1=∠2,则图中全等三角形共有( )



















