试卷题目
1.如图是科学防控新冠肺炎病毒传染的宣传图片,图片上有图案和文字说明,其中图案是轴对称图形的是( )
- A.

打喷嚏 捂口鼻 - B.

喷嚏后 慎揉眼 - C.

勤洗手 勤通风 - D.

戴口罩 讲卫生
2.三角形两边的长度分别是20cm和30cm,要组成一个三角形,则应在下列四条线段中选取( )的线段.
- A. 10cm
- B. 40cm
- C. 50cm
- D. 60cm
3.已知a≠0,下列计算正确的是( )
- A. a2+a3=a5
- B. a2•a3=a6
- C. (a2)3=a5
- D. a3÷a2=a
4.如果一个正多边形的每一个外角都是45°,那么这个正多边形的内角和为( )
- A. 360°
- B. 720°
- C. 1080°
- D. 1440°
5.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.
如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )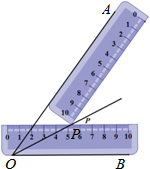
如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

- A. 角的内部到角的两边的距离相等的点在角的平分线上
- B. 角平分线上的点到这个角两边的距离相等
- C. 三角形三条角平分线的交点到三条边的距离相等
- D. 以上均不正确
6.如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )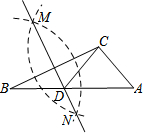
| 1 |
| 2 |

- A. 105°
- B. 100°
- C. 95°
- D. 90°
7.如图,四边形ABCD是一个长方形,利用不同的方法可以计算出长方形的面积.通过分析图形中所标线段的长度,将多项式m2+3mn+2n2因式分解,其结果正确的是( )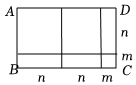

- A. (m+2n)2
- B. (m+2n)(m+n)
- C. (2m+n)(m+n)
- D. (m+2n)(m-n)
8.如图,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC成轴对称且以格点为顶点三角形共有( )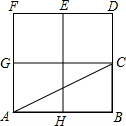

- A. 3个
- B. 4个
- C. 5个
- D. 6个
9.我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则符合题意的方程是( )
- A. 3(x-1)=
6210 x - B. =3
6210 x-1 - C. 3x-1=
6210 x - D. =3
6210 x
10.现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )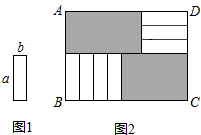

- A. a=2b
- B. a=3b
- C. a=3.5b
- D. a=4b
11.要使分式
有意义,则x须满足的条件为 .
| 2x |
| x+1 |
12.已知点A(x,-4)与点B(3,y)关于x轴对称,那么x+y的值为 .
13.如图所示,已知AC=DB,要证明△ABC≌△DCB,则还需要添加一个条件是 .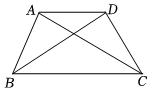

14.如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=32°,则∠CDE= .

15.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,BD是△ABC的角平分线,点P,点N分别是BD,AC边上的动点,点M在BC上,且BM=1,则PM+PN的最小值为 .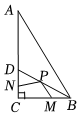

16.(1)计算:(3x+1)(3x-1)-(x+3)2;
(2)解方程:
+
=1.
(2)解方程:
| x |
| x-3 |
| 2-x |
| 3-x |
17.先化简,再求值:(
-1)÷
,其中x=2021.
| 1 |
| x+1 |
| x2-1 |
| x2+2x+1 |
18.如图所示,CD和EF是两条互相垂直的道路,A、B是某公司的两个销售点,公司要在P处修建一个货运站,使P到两条道路的距离相等,且到A、B两个销售点的距离相等,请作出一个符合条件点P的位置.(尺规作图,保留作图痕迹,不写作法)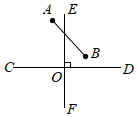

19.阅读理解:阅读下列材料:已知二次三项式2x2+x+a有一个因式是(x+2),求另一个因式以及a的值.
解:设另一个因式是(2x+b),
根据题意,得2x2+x+a=(x+2)(2x+b).
展开,得2x2+x+a=2x2+(b+4)x+2b.
所以,
,解得
所以,另一个因式是(2x-3),a的值是-6.
请你仿照以上做法解答下题:已知二次三项式3x2+10x+m有一个因式是(x+4),求另一个因式以及m的值.
解:设另一个因式是(2x+b),
根据题意,得2x2+x+a=(x+2)(2x+b).
展开,得2x2+x+a=2x2+(b+4)x+2b.
所以,
| { | b+4=1 a=2b |
| { | a=−6 b=−3 |
所以,另一个因式是(2x-3),a的值是-6.
请你仿照以上做法解答下题:已知二次三项式3x2+10x+m有一个因式是(x+4),求另一个因式以及m的值.
20.如图,已知AB=DC,AB∥CD、E、F是AC上两点,且AF=CE,
(1)△ABE与△CDF是否全等,并说明理由;
(2)连接BC,若∠CFD=80°,∠BCE=25°,求∠CBE的度数.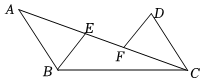
(1)△ABE与△CDF是否全等,并说明理由;
(2)连接BC,若∠CFD=80°,∠BCE=25°,求∠CBE的度数.

21.近年来节能又环保的油电混合动力汽车越来越受到人们的喜爱,某品牌油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为75元;若完全用电做动力行驶,则费用为30元.已知汽车行驶中每千米用油费用比用电费用多0.3元,汽车行驶中每千米用电费用是多少元?甲、乙两地的距离是多少千米?
22.如图,△ABC中,AB=AC,∠B=30°,点O在BC边上运动(O不与B,C重合),点D在线段AB上,连结AO、OD.点O运动时,始终满足∠AOD=∠B.
(1)当OD∥AC时,判断△AOB的形状并说明理由;
(2)当AO的最小值为4时,此时BD= ;
(3)在点O的运动过程中,△AOD的形状是等腰三角形时,请求出此时∠BDO的度数.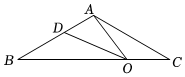
(1)当OD∥AC时,判断△AOB的形状并说明理由;
(2)当AO的最小值为4时,此时BD= ;
(3)在点O的运动过程中,△AOD的形状是等腰三角形时,请求出此时∠BDO的度数.

23.如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数(直接写出结果);
(3)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.
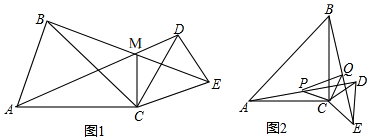
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数(直接写出结果);
(3)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.






