试卷题目
1．下列长度的三条线段能组成三角形的是( )
- A. 4，5，9
- B. 5，5，11
- C. 1，2，3
- D. 5，6，10
2．如图，AB=DB，BC=BE，欲证△ABE≌△DBC，则可增加的条件是( )
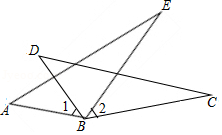
- A. ∠ABE=∠DBE
- B. ∠A=∠D
- C. ∠E=∠C
- D. ∠1=∠2
3．已知等腰△ABC的周长为18cm，BC=8cm，若△ABC与△A′B′C′全等，则△A′B′C′的腰长等于( )
- A. 8cm
- B. 2cm或8cm
- C. 5cm
- D. 8cm或5cm
4．下列说法正确的是( )
- A. 等腰三角形的高、中线、角平分线互相重合
- B. 顶角相等的两个等腰三角形全等
- C. 等腰三角形的两个底角相等
- D. 等腰三角形一边不可以是另一边的2倍
5．如图OP平分∠AOB，PC⊥OA于C，D在OB上，PC=3，则PD的大小关系是( )
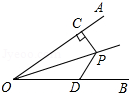
- A. PD≥3
- B. PD=3
- C. PD≤3
- D. 不能确定
6．如图，四边形ABCD中，若去掉一个60°的角后得到一个五边形，则∠1+∠2等于( )
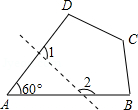
- A. 120°
- B. 180°
- C. 240°
- D. 300°
7．如图，在平面直角坐标系中，在x轴、y轴的正半轴上分别截取OA、OB，使OA=OB；再分别以点A、B为圆心，以大于
AB长为半径作弧，两弧交于点C．若点C的坐标为(m-1，2n)，则m与n的关系为( )
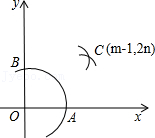
| 1 |
| 2 |
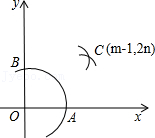
- A. m+2n=1
- B. m-2n=1
- C. 2n-m=1
- D. n-2m=1
8．下列图形一定是轴对称图形的是( )
- A. 平行四边形
- B. 正方形
- C. 三角形
- D. 梯形
9．如图∠E=∠F=90°，∠B=∠C，AE=AF，给出下列结论：①∠1=∠2；②BE=CF；③△ACN≌△ABM；④CD=DN．其中正确的结论有( )
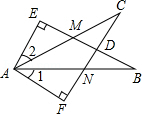
- A. 1个
- B. 2个
- C. 3个
- D. 4个
10．如图，在△ABC中，AD是∠A的外角平分线，P是AD上异于A的任意一点，设PB=m，PC=n，AB=c，AC=b，则(m+n)与(b+c)的大小关系是( )
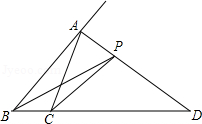
- A. m+n>b+c
- B. m+n
- C. m+n=b+c
- D. 无法确定
11．已知点P(3，-1)关于y轴的对称点Q的坐标是(a+b，1-b)，则ab的值为 ．
12．在△ABC中，D、E分别是BC、AD的中点，S△ABC=4cm2，则S△ABE= ．
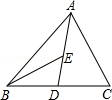
13．等腰三角形底边长为6cm，一腰上的中线把它的周长分成两部分的差为2cm，则腰长为 ．
14．如图，点D，E，F，B在同一条直线上，AB//CD，AE//CF且AE=CF，若BD=10，BF=3.5，则EF= ．
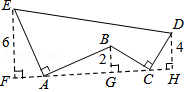
15．如图，AE⊥AB，且AE=AB，BC⊥CD，且BC=CD，请按照图中所标注的数据计算图中实线所围成的图形的面积S= ．
16．在平面直角坐标系中，已知A(1，1)，B(8，0)，C(-1，1)，O是坐标原点，如果△OAB≌△OCD，则点D的坐标是 ．
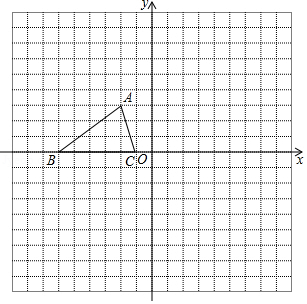
17．(1)直接写出A点关于y轴对称的点的坐标是 ．
(2)将△ABC向右平移六个单位后得△A1B1C1，则线段AB平移扫过的面积是 ．
(3)作出△A1B1C1关于x轴对称的图形△A2B2C2，画出△A2B2C2，连接A2B交y轴于点D，直接写出D点的坐标 ．
(2)将△ABC向右平移六个单位后得△A1B1C1，则线段AB平移扫过的面积是 ．
(3)作出△A1B1C1关于x轴对称的图形△A2B2C2，画出△A2B2C2，连接A2B交y轴于点D，直接写出D点的坐标 ．
18．若一个正多边形的周长为48cm，且它的内角和为720°，求这个正多边形的边长．
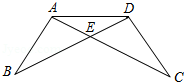
19．一次数学课上，老师在黑板上画了如图图形，并写下了四个等式：
①BD=CA，②AB=DC，③∠B=∠C，④∠BAE=∠CDE．
要求同学从这四个等式中选出两个作为条件，推出AE=DE．请你试着完成老师提出的要求，并说明理由．(写出一种即可)
已知：________(请填写序号)，求证：AE=DE．
证明：
①BD=CA，②AB=DC，③∠B=∠C，④∠BAE=∠CDE．
要求同学从这四个等式中选出两个作为条件，推出AE=DE．请你试着完成老师提出的要求，并说明理由．(写出一种即可)
已知：________(请填写序号)，求证：AE=DE．
证明：
20．如图，BD平分∠ABC交AC于点D，DE⊥AB于E，DF⊥BC于F，AB=6，BC=8，若S△ABC=28，求DE的长．
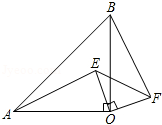
21．如图，已知，等腰△OAB中，∠AOB=90°，等腰△EOF中，∠EOF=90°，连接AE、BF．求证：
(1)AE=BF；
(2)AE⊥BF．
(1)AE=BF；
(2)AE⊥BF．
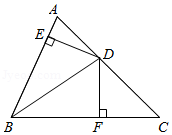
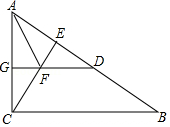
22．如图，在△ABC中，∠ACB=90°，CE⊥AB于点E，AD=AC，AF平分∠CAB交CE于点F，DF的延长线交AC于点G，
求证：(1)DF//BC；
(2)FG=FE．
求证：(1)DF//BC；
(2)FG=FE．
23．观察下列等式：
12×231=132×21，
13×341=143×31，
23×352=253×32，
34×473=374×43，
62×286=682×26，
…
以上每个等式中两边数字是分别对称的，且每个等式中组成两位数与三位数的数字之间具有相同规律，我们称这类等式为“数字对称等式”．
(1)根据上述各式反映的规律填空，使式子称为“数字对称等式”：
①52× = ×25；
② ×396=693× ．
(2)设这类等式左边两位数的十位数字为a，个位数字为b，且2≤a+b≤9，写出表示“数字对称等式”一般规律的式子(含a、b)，并证明．
12×231=132×21，
13×341=143×31，
23×352=253×32，
34×473=374×43，
62×286=682×26，
…
以上每个等式中两边数字是分别对称的，且每个等式中组成两位数与三位数的数字之间具有相同规律，我们称这类等式为“数字对称等式”．
(1)根据上述各式反映的规律填空，使式子称为“数字对称等式”：
①52× = ×25；
② ×396=693× ．
(2)设这类等式左边两位数的十位数字为a，个位数字为b，且2≤a+b≤9，写出表示“数字对称等式”一般规律的式子(含a、b)，并证明．
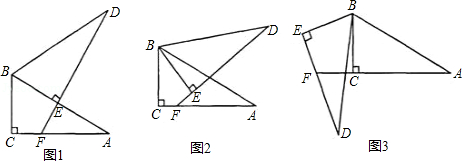
24．将两个全等的直角三角形ABC和DBE按图(1)方式摆放，其中∠ACB=∠DEB=90°，∠A=∠D=30°，点E落在AB上，DE所在直线交AC所在直线于点F．
(1)求证：CF=EF；
(2)若将图(1)中的△DBE绕点B按顺时针方向旋转角a，且0° DE．(填“>”或“=”或“<” )
(3)若将图(1)中△DBE的绕点B按顺时针方向旋转角β，且60°<β<180°，其他条件不变，如图(3)．请你写出此时AF、EF与DE之间的关系，并加以证明．
(1)求证：CF=EF；
(2)若将图(1)中的△DBE绕点B按顺时针方向旋转角a，且0° DE．(填“>”或“=”或“<” )
(3)若将图(1)中△DBE的绕点B按顺时针方向旋转角β，且60°<β<180°，其他条件不变，如图(3)．请你写出此时AF、EF与DE之间的关系，并加以证明．
