试卷题目
1.下列冰雪运动项目的图标中,是轴对称图形的是( )
- A.

- B.

- C.

- D.

2.2021年10月16日,我国神舟十三号载人飞船与天和核心舱首次成功实现“径向对接”,对接过程的控制信息通过微波传递.微波理论上可以在0.000003秒内接收到相距约1千米的信息.将数字0.000003用科学记数法表示应为( )
- A. 30×10-3
- B. 3×10-6
- C. 3×10-5
- D. 0.3×10-4
3.下列变形是因式分解的是( )
- A. x(x+1)=x2+x
- B. x2+6x+4=(x+3)2-5
- C. x2+xy-3=x(x+y)-3
- D. x2+2x+1=(x+1)2
4.下列计算正确的是( )
- A. (3a3)2=9a6
- B. a3+a2=2a5
- C. a3•a2=a6
- D. a8÷a2=a4
5.如图,△ABC是等边三角形,D是BC边上一点,DE⊥AC于点E.若EC=3,则DC的长为( )
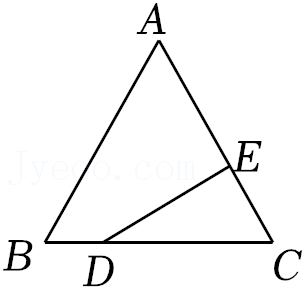
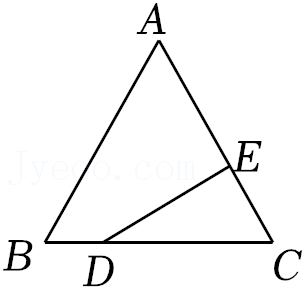
- A. 4
- B. 5
- C. 6
- D. 7
6.下列变形正确的是( )
- A. =
y x y+3 x+3 - B. =
y x -y -x - C. =
y x y2 x2 - D. =
y x x y
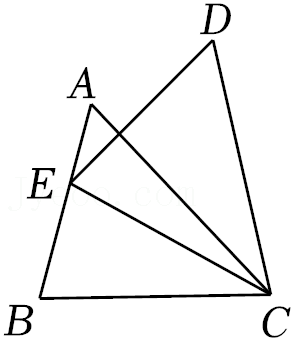
7.如图,△ABC≌△DEC,点E在线段AB上,∠B=75°,则∠ACD的度数为( )

- A. 20°
- B. 25°
- C. 30°
- D. 40°
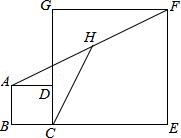
8.某中学开展“筑梦冰雪,相约冬奥”的学科活动,设计几何图形作品表达对冬奥会的祝福.小冬以长方形ABCD的四条边为边向外作四个正方形,设计出“中”字图案,如图所示.若四个正方形的周长之和为24,面积之和为12,则长方形ABCD的面积为( )
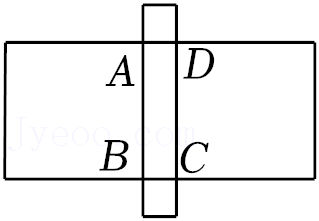

- A. 1
- B.
3 2 - C. 2
- D.
8 3
9.若分式
有意义,则x的取值范围为 .
| 1 |
| x-2 |
10.在平面直角坐标系xOy中,点A(2,4)与点B关于y轴对称,则点B的坐标是 .
11.分解因式:3a2-12= .
12.若x=4是关于x的方程
=3的解,则m的值为 .
| 2x-m |
| x-3 |
13.等腰三角形的一个角等于40°,则它的顶角的度数是 .
14.在〇处填入一个整式,使关于x的多项式x2+〇+1可以因式分解,则〇可以为 .(写出一个即可)
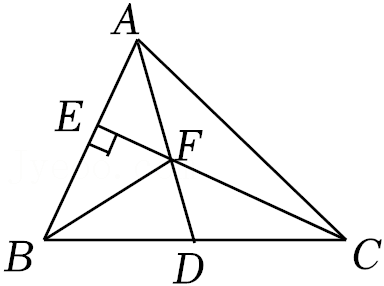
15.如图,在△ABC中,AD为BC边上的中线,CE⊥AB于点E,AD与CE交于点F,连接BF.若BF平分∠ABC,EF=2,BC=8,则△CDF的面积为 .

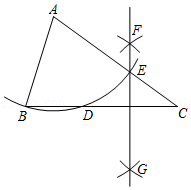
16.如图,在△ABC中,AC=BC,以点A为圆心,AB长为半径作弧交BC于点D,交AC于点E.再分别以点C,D为圆心,大于
CD的长为半径作弧,两弧相交于F,G两点.作直线FG,若直线FG经过点E,则∠AEG的度数为 °.
| 1 |
| 2 |

17.计算:(-π)0+(
)-1-28÷26.
| 1 |
| 3 |
18.化简:(x-2)2+(x+3)(x+1).
19.化简:[(x+3y)(x-3y)-x2]÷9y.
20.解方程:
=
| 1 |
| x |
| 5 |
| x+3 |
21.如图,已知线段AB及线段AB外一点C,过点C作直线CD,使得CD⊥AB.
小欣的作法如下:
①以点B为圆心,BC长为半径作弧;
②以点A为圆心,AC长为半径作弧,两弧交于点D;
③作直线CD.
则直线CD即为所求.
(1)根据小欣的作图过程补全图形;
(2)完成下面的证明.
证明:连接AC,AD,BC,BD.
∵BC=BD,
∴点B在线段CD的垂直平分线上.( )(填推理的依据)
∵AC= ,
∴点A在线段CD的垂直平分线上.
∴直线AB为线段CD的垂直平分线.
∴CD⊥AB.
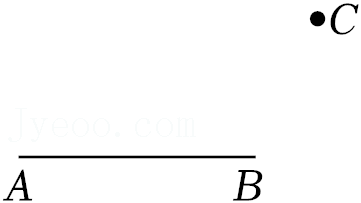
小欣的作法如下:
①以点B为圆心,BC长为半径作弧;
②以点A为圆心,AC长为半径作弧,两弧交于点D;
③作直线CD.
则直线CD即为所求.
(1)根据小欣的作图过程补全图形;
(2)完成下面的证明.
证明:连接AC,AD,BC,BD.
∵BC=BD,
∴点B在线段CD的垂直平分线上.( )(填推理的依据)
∵AC= ,
∴点A在线段CD的垂直平分线上.
∴直线AB为线段CD的垂直平分线.
∴CD⊥AB.
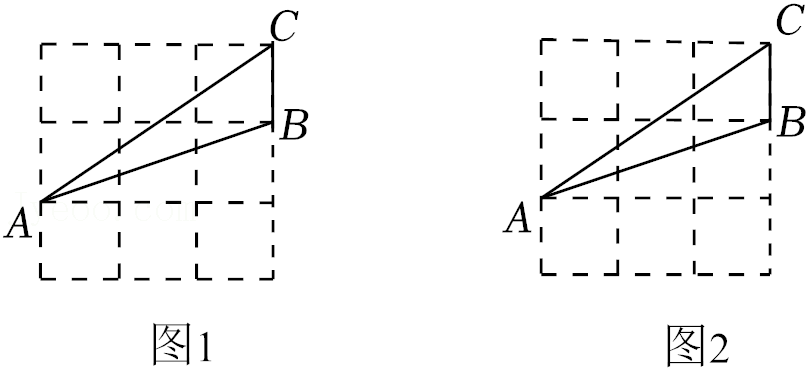
22.在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中△ABC是一个格点三角形.请在图1和图2中各画出一个与△ABC成轴对称的格点三角形,并画出对称轴.

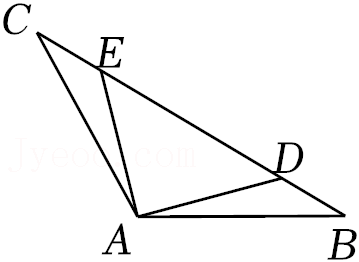
23.如图,在△ABC中,∠B=∠C,点D,E在BC边上,AD=AE.求证:CD=BE.

24.已知a2+2a-1=0,求代数式(
-
)÷
的值.
| a2-1 |
| a2-2a+1 |
| 1 |
| 1-a |
| 1 |
| a2-a |
25.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需要的时间与原计划生产450台机器所需要的时间相同,现在平均每天生产多少台机器?
26.如图1,在平面直角坐标系xOy中,点A(-4,0),B(4,0),C(0,4),给出如下定义:若P为△ABC内(不含边界)一点,且AP与△BCP的一条边相等,则称P为△ABC的友爱点.
(1)在P1(0,3),P2(-1,1),P3(-2,1)中,△ABC的友爱点是 .
(2)如图2,若P为△ABC内一点,且∠PAB=∠PCB=15°,求证:P为△ABC的友爱点;
(3)直线l为过点M(0,m)且与x轴平行的直线,若直线l上存在△ABC的三个友爱点,直接写出m的取值范围是 .
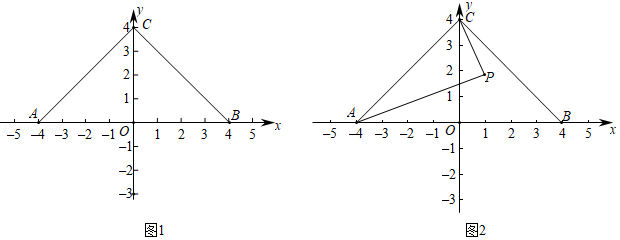
(1)在P1(0,3),P2(-1,1),P3(-2,1)中,△ABC的友爱点是 .
(2)如图2,若P为△ABC内一点,且∠PAB=∠PCB=15°,求证:P为△ABC的友爱点;
(3)直线l为过点M(0,m)且与x轴平行的直线,若直线l上存在△ABC的三个友爱点,直接写出m的取值范围是 .
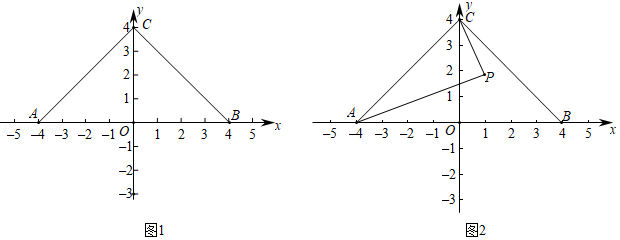
27.在分式
中,若M,N为整式,分母M的次数为a,分子N的次数为b(当N为常数时,b=0),则称分式
为(a-b)次分式.例如,
为三次分式.
(1)请写出一个只含有字母x的二次分式 ;
(2)已知A=
,B=
(其中m,n为常数).
①若m=0,n=-5,则A•B,A+B,A-B,A2中,化简后是二次分式的为 ;
②若A与B的和化简后是一次分式,且分母的次数为1,求2m+n的值.
| N |
| M |
| N |
| M |
| x+1 |
| x4-x3 |
(1)请写出一个只含有字母x的二次分式 ;
(2)已知A=
| mx+2 |
| x-3 |
| nx+3 |
| x2-9 |
①若m=0,n=-5,则A•B,A+B,A-B,A2中,化简后是二次分式的为 ;
②若A与B的和化简后是一次分式,且分母的次数为1,求2m+n的值.
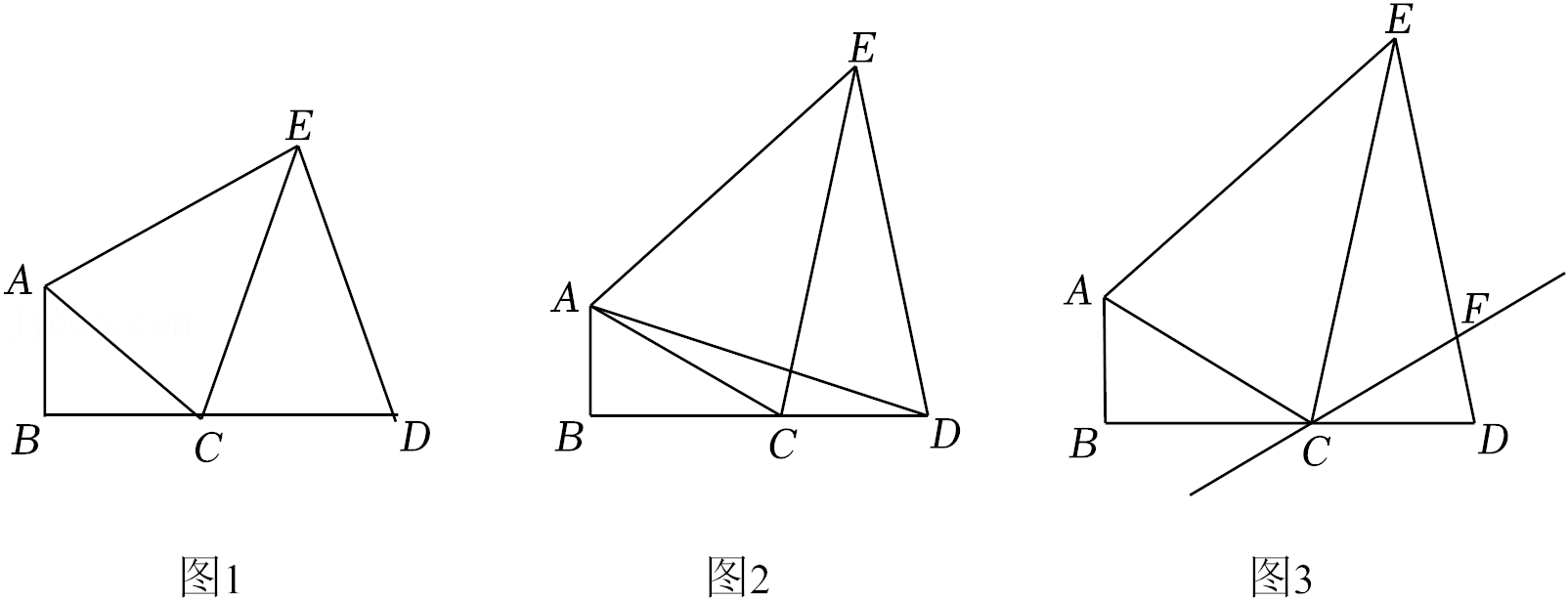
28.在△ABC中,∠B=90°,D为BC延长线上一点,点E为线段AC,CD的垂直平分线的交点,连接EA,EC,ED.
(1)如图1,当∠BAC=50°时,则∠AED= °;
(2)当∠BAC=60°时,
①如图2,连接AD,判断△AED的形状,并证明;
②如图3,直线CF与ED交于点F,满足∠CFD=∠CAE.P为直线CF上一动点.当PE-PD的值最大时,用等式表示PE,PD与AB之间的数量关系为 ________,并证明.
(1)如图1,当∠BAC=50°时,则∠AED= °;
(2)当∠BAC=60°时,
①如图2,连接AD,判断△AED的形状,并证明;
②如图3,直线CF与ED交于点F,满足∠CFD=∠CAE.P为直线CF上一动点.当PE-PD的值最大时,用等式表示PE,PD与AB之间的数量关系为 ________,并证明.