试卷题目
1.下列图形中,不是轴对称图形的是( )
- A.

- B.

- C.

- D.

2.若一个三角形的两边长分别为3和7,则第三边长可能是( )
- A. 6
- B. 3
- C. 2
- D. 11
3.平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于( )
- A. y轴对称
- B. x轴对称
- C. 原点对称
- D. 直线y=x对称
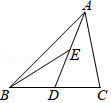
4.如图,△ABC中,D、E分别是BC、AD的中点,若△ABC的面积是18,则△ABE的面积是( )

- A. 9
- B. 6
- C. 4.5
- D. 4
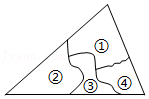
5.打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )

- A. 带①②去
- B. 带②③去
- C. 带③④去
- D. 带②④去
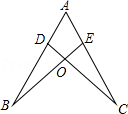
6.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )

- A. ∠B=∠C
- B. AD=AE
- C. BD=CE
- D. BE=CD
7.等腰三角形一腰上的高与另一腰的夹角为60°,则顶角的度数为( )
- A. 30°
- B. 30°或150°
- C. 60°或150°
- D. 60°或120°
8.如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )


- A. 140米
- B. 150米
- C. 160米
- D. 240米
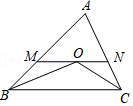
9.如图,在△ABC中,BO平分∠ABC,CO平分∠ACB,MN经过点O,与AB、AC相交于点M、N,且MN∥BC.若AB=8,AC=6,BC=10,那么△AMN的周长是( )

- A. 7
- B. 12
- C. 14
- D. 24
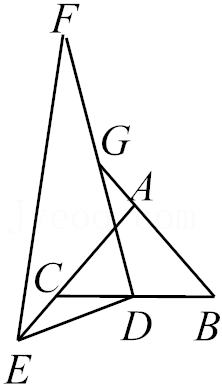
10.如图,△ABC是等腰直角三角形,△DEF是直角三角形,且∠F=30°,将D放在斜边BC的中点处,转动△DEF,设DE,DF分别交AC,BA的延长线于E,G,则下列结论:①AG=CE;②BG-AC=CE;③S△BDG-S△CDE=
S△ABC;④EF+2FG=2FD,其中成立的是( )
| 1 |
| 2 |

- A. ①②③
- B. ①②③④
- C. ②③④
- D. ①②④
11.空调安装在墙上时,一般都会采用如图所示的方法固定,这种方法应用的几何原理是 .
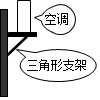

12.等腰三角形周长为16cm,一边长为4cm,该等腰三角形的底边长为 cm.
13.如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD= .
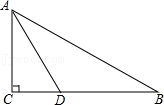

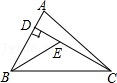
14.如图,已知在△ABC中,CD是AB边上的高,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于 .

15.如图,在△ABC中,AB=3,AC=4,BC=5,EF垂直平分BC,点P为直线EF上一动点,则△ABP周长的最小值是 .















