试卷题目
1.下列图案中,可以看成轴对称图形的是( )
- A.

- B.

- C.

- D.

2.下列运算中,结果正确的是( )
- A. (a2)3=a5
- B. (3a)2=6a2
- C. a6÷a2=a3
- D. a2•a3=a5
3.在△ABC中,作出AC边上的高,正确的是( )
- A.

- B.

- C.

- D.

4.如图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在一个角的顶点,AB和AD沿着这个角的两边放下,利用全等三角形的性质就能说明射线AC是这个角的平分线,这里判定△ABC和△ADC是全等三角形的依据是( )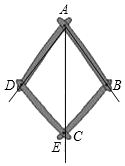

- A. SSS
- B. ASA
- C. SAS
- D. AAS
5.下列分式中,从左到右变形错误的是( )
- A. =
c 4c 1 4 - B. +
1 a =1 b 1 a+b - C. =-
1 a-b 1 b-a - D. =
a2-4 a2+4a+4 a-2 a+2
6.已知三条线段的长分别是4,4,m,若它们能构成三角形,则整数m的最大值是( )
- A. 10
- B. 8
- C. 7
- D. 4
7.某校八年级一班计划安排一次以“迎冬奥”为主题的知识竞赛,班主任王老师打算到某文具店购买一些笔记本作为竞赛用的奖品.目前该文具店正在搞优惠酬宾活动:购买同样的笔记本,当花费超过20元时,每本便宜1元.已知王老师花费24元比花费20元多买了2本笔记本,求他花费24元买了多少本笔记本.设他花费24元买了x本笔记本,根据题意可列方程( )
- A. -
24 x =120 x-2 - B. -
24 x-2 =120 x - C. -
20 x-2 =124 x - D. -
20 x+2 =124 x
8.在平面直角坐标系xOy中,点A(0,2),B(a,0),C(m,n)(n>0).若△ABC是等腰直角三角形,且AB=BC,当0<a<1时,点C的横坐标m的取值范围是( )
- A. 0<m<2
- B. 2<m<3
- C. m<3
- D. m>3
9.计算:
(1)2-1= ;
(2)(π-1)0= .
(1)2-1= ;
(2)(π-1)0= .
10.若分式
有意义,则x的取值范围为 .
| 1 |
| x-2 |
11.若一个多边形的内角和是540°,则这个多边形是 边形.
12.计算:2ab(3a2-5b)= .
13.若a2+ka+9是一个完全平方式,则常数k= .
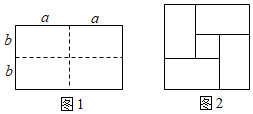
14.如图1,将一个长为2a,宽为2b的长方形沿图中虚线剪开分成四个完全相同的小长方形,然后将这四个完全相同的小长方形拼成一个正方形(如图2).设图2中的大正方形面积为S1,小正方形面积为S2,则S1-S2的结果是 (用含a,b的式子表示)

15.如图,在平面直角坐标系xOy中,点A(2,0),B(4,2),若点P在x轴下方,且以O,A,P为顶点的三角形与△OAB全等,则满足条件的P点的坐标是 .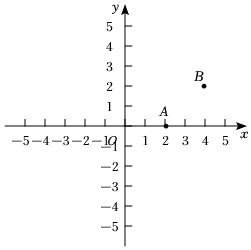

16.如图,Rt△ABC中,∠ACB=90°,∠B=30°,AC=2.D为BC上一动点,连接AD,AD的垂直平分线分别交AC,AB于点E,F,则线段BF长的最大值是 .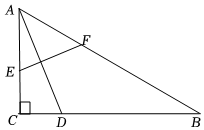

17.分解因式:
(1)3a2-6ab+3b2;
(2)x2(m-2)+y2(2-m).
(1)3a2-6ab+3b2;
(2)x2(m-2)+y2(2-m).
18.(1)计算:(x-8y)(x+y);
(2)先化简,再求值:(a+1-
)÷
,其中a=-3.
(2)先化简,再求值:(a+1-
| 3 |
| a-1 |
| a2−4 |
| a2−2a+1 |
19.解方程:
-
=1.
| x-1 |
| x+1 |
| 2 |
| x2-1 |
20.如图,点A,B,C,D在一条直线上,AE∥DF,AE=DF,AB=CD.
(1)求证:△AEC≌△DFB.
(2)若∠A=40°,∠ECD=145°,求∠F的度数.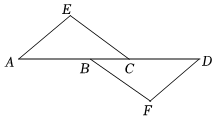
(1)求证:△AEC≌△DFB.
(2)若∠A=40°,∠ECD=145°,求∠F的度数.

21.如图,8×12的长方形网格中,网格线的交点叫做格点,点A,B,C都是格点.请按要求解答下列问题:
平面直角坐标系xOy中,点A,B的坐标分别是(-3,1),(-1,4),
(1)①请在图中画出平面直角坐标系xOy;
②点C的坐标是 ,点C关于x轴的对称点C1的坐标是 .
(2)设l是过点C且平行于y轴的直线,
①点A关于直线l的对称点A1的坐标是 ;
②在直线l上找一点P,使PA+PB最小,在图中标出此时点P的位置;
③若Q(m,n)为网格中任一格点,直接写出点Q关于直线l的对称点Q1的坐标(用含m,n的式子表示).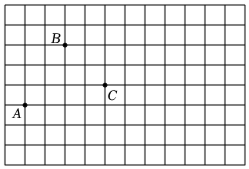
平面直角坐标系xOy中,点A,B的坐标分别是(-3,1),(-1,4),
(1)①请在图中画出平面直角坐标系xOy;
②点C的坐标是 ,点C关于x轴的对称点C1的坐标是 .
(2)设l是过点C且平行于y轴的直线,
①点A关于直线l的对称点A1的坐标是 ;
②在直线l上找一点P,使PA+PB最小,在图中标出此时点P的位置;
③若Q(m,n)为网格中任一格点,直接写出点Q关于直线l的对称点Q1的坐标(用含m,n的式子表示).

22.已知:如图1,线段a,b(a>b).
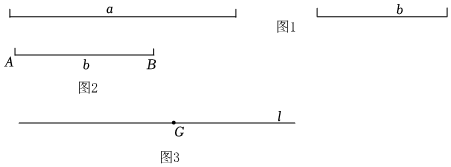
(1)求作:等腰△ABC,使得它的底边长为b,底边上的高的长为a.
作法:①作线段AB=b.
②作线段AB的垂直平分线MN,与AB相交于点D.
③在MN上取一点C,使DC=a.
④连接AC,BC,则△ABC就是所求作的等腰三角形.
用直尺和圆规在图2中补全图形(要求:保留作图痕迹);
(2)求作:等腰△PEF,使得它的腰长为线段a,b中一条线段的长,底边上的高的长为线段a,b中另一条线段的长.
作法:①作直线l,在直线l上取一点G.
②过点G作直线l的垂线GH.
③在GH上取一点P,使PG=________.
④以P为圆心,以 ________的长为半径画弧,与直线l分别相交于点E,F.
⑤连接PE,PF,则△PEF就是所求作的等腰三角形.
请补全作法,并用直尺和圆规在图3中补全图形(要求:保留作图痕迹).

(1)求作:等腰△ABC,使得它的底边长为b,底边上的高的长为a.
作法:①作线段AB=b.
②作线段AB的垂直平分线MN,与AB相交于点D.
③在MN上取一点C,使DC=a.
④连接AC,BC,则△ABC就是所求作的等腰三角形.
用直尺和圆规在图2中补全图形(要求:保留作图痕迹);
(2)求作:等腰△PEF,使得它的腰长为线段a,b中一条线段的长,底边上的高的长为线段a,b中另一条线段的长.
作法:①作直线l,在直线l上取一点G.
②过点G作直线l的垂线GH.
③在GH上取一点P,使PG=________.
④以P为圆心,以 ________的长为半径画弧,与直线l分别相交于点E,F.
⑤连接PE,PF,则△PEF就是所求作的等腰三角形.
请补全作法,并用直尺和圆规在图3中补全图形(要求:保留作图痕迹).
23.(1)如果(x-3)(x+2)=x2+mx+n,那么m的值是 ,n的值是 ;
(2)如果(x+a)(x+b)=x2-2x+
,
①求(a-2)(b-2)的值;
②求
+
+1的值.
(2)如果(x+a)(x+b)=x2-2x+
| 1 |
| 2 |
①求(a-2)(b-2)的值;
②求
| 1 |
| a2 |
| 1 |
| b2 |
24.在△ABC中,∠BAC=120°,AB=AC,AD为△ABC的中线,点E是射线AD上一动点,连接CE,作∠CEM=60°,射线EM与射线BA交于点F.
(1)如图1,当点E与点D重合时,求证:AB=2AF;
(2)如图2,当点E在线段AD上,且与点A,D不重合时,
①依题意,补全图形;
②用等式表示线段AB,AF,AE之间的数量关系,并证明.
(3)当点E在线段AD的延长线上,且ED≠AD时,直接写出用等式表示的线段AB,AF,AE之间的数量关系.

(1)如图1,当点E与点D重合时,求证:AB=2AF;
(2)如图2,当点E在线段AD上,且与点A,D不重合时,
①依题意,补全图形;
②用等式表示线段AB,AF,AE之间的数量关系,并证明.
(3)当点E在线段AD的延长线上,且ED≠AD时,直接写出用等式表示的线段AB,AF,AE之间的数量关系.

25.观察下列等式:
①1-1-
=-
;
②
-
-
=-
;
③
-
-
=-
;
④
-
-
=-
;
…
根据上述规律回答下列问题:
(1)第⑤个等式是 ;
(2)第n个等式是 (用含n的式子表示,n为正整数).
①1-1-
| 1 |
| 2 |
| 1 |
| 1×2 |
②
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3×4 |
③
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 5×6 |
④
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 8 |
| 1 |
| 7×8 |
…
根据上述规律回答下列问题:
(1)第⑤个等式是 ;
(2)第n个等式是 (用含n的式子表示,n为正整数).
26.对于面积为S的三角形和直线l,将该三角形沿直线l折叠,重合部分的图形面积记为S0,定义
为该三角形关于直线l的对称度.如图,将面积为S的△ABC沿直线l折叠,重合部分的图形为△C′DE,将△C′DE的面积记为S0,则称
为△ABC关于直线l的对称度.
在平面直角坐标系xOy中,点A(0,3),B(-3,0),C(3,0).
(1)过点M(m,0)作垂直于x轴的直线l1,
①当m=1时,△ABC关于直线l1的对称度的值是 ;
②若△ABC关于直线l1的对称度为1,则m的值是 .
(2)过点N(0,n)作垂直于y轴的直线l2,求△ABC关于直线l2的对称度的最大值.
(3)点P(-4,0)满足AP=5,点Q的坐标为(t,0),若存在直线,使得△APQ关于该直线的对称度为1,写出所有满足题意的整数t的值.
| S0 |
| S-S0 |
| S0 |
| S-S0 |
在平面直角坐标系xOy中,点A(0,3),B(-3,0),C(3,0).
(1)过点M(m,0)作垂直于x轴的直线l1,
①当m=1时,△ABC关于直线l1的对称度的值是 ;
②若△ABC关于直线l1的对称度为1,则m的值是 .
(2)过点N(0,n)作垂直于y轴的直线l2,求△ABC关于直线l2的对称度的最大值.
(3)点P(-4,0)满足AP=5,点Q的坐标为(t,0),若存在直线,使得△APQ关于该直线的对称度为1,写出所有满足题意的整数t的值.






