试卷题目
1.如所示图形中轴对称图形是( )
- A.

- B.

- C.

- D.

2.点A(3,-1)关于x轴的对称点是( )
- A. (-1,3)
- B. (-3,-1)
- C. (3,-1)
- D. (3,1)
3.如图,△ABC沿AB向下翻折得到△ABD,若∠ABC=30°,∠ADB=100°,则∠BAC的度数是( )
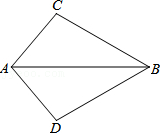

- A. 100°
- B. 30°
- C. 50°
- D. 80°
4.有两根长度分别为2,10的木棒,若想钉一个三角形木架,第三根木棒的长度可以是( )
- A. 12
- B. 10
- C. 8
- D. 6
5.下列判断中错误的是( )
- A. 有两角和其中一个角的对边对应相等的两个三角形全等
- B. 有一边相等的两个等边三角形全等
- C. 有两边和一角对应相等的两个三角形全等
- D. 有两边和其中一边上的中线对应相等的两个三角形全等
6.若正多边形的一个外角是36°,则该正多边形的内角和为( )
- A. 360°
- B. 720°
- C. 1440°
- D. 1800°
7.已知等腰三角形的一个内角为40°,则这个等腰三角形的顶角为( )
- A. 40°
- B. 100°
- C. 40°或70°
- D. 40°或100°
8.如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为( )
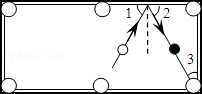

- A. 30°
- B. 45°
- C. 60°
- D. 75°
9.如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为( )
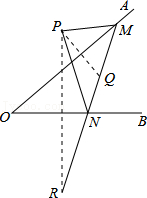

- A. 4.5cm
- B. 5.5cm
- C. 6.5cm
- D. 7cm
10.如图所示的“钻石”型网格(由边长都为1个单位长度的等边三角形组成),其中已经涂黑了3个小三角形(阴影部分表示),请你再只涂黑一个小三角形,使它与阴影部分合起来所构成的图形是一个轴对称图形,一共有( )种涂法.
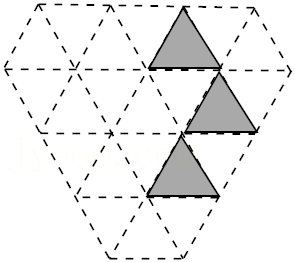

- A. 1
- B. 2
- C. 3
- D. 4
11.计算-(-2a2b)4= .
12.如图,△ABC≌△AED,若AB=AE,∠1=27°,则∠2= °.
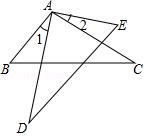

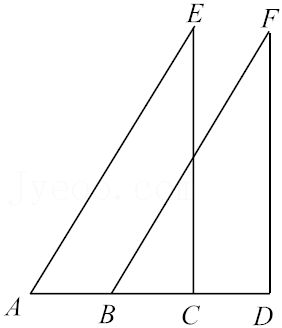
13.如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上.若想知道两点A,B的距离,只需要测量出线段 即可.
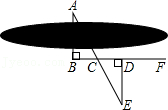

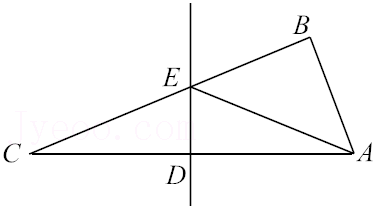
14.如图,已知直线AB∥CD,∠C=115°,∠A=25°,则∠E= 度.
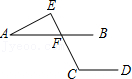

15.如图,BD平分∠ABC,DE∥BC交BA于点E,若DE=1,则EB= .


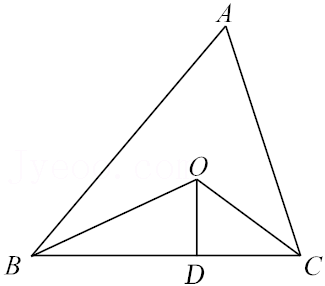
16.如图,在△ABC中,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,若△ABC的周长是20,且OD=3,则△ABC的面积为 .

17.平面直角坐标系xOy中,点A(4,3),点B(3,0),点C(5,3),点E在x轴上.当CE=AB时,点E的坐标为 .
18.已知等边△ABC的边长为6,点M是射线AB上的动点,点N是边BC延长线上的动点,在运动的过程中始终满足AM=CN,作MD垂直于射线AC于D,连接MN交射线AC于E.
(1)如图1,当点M为AB的三等分点(靠近点A)时,DE的长为 .
(2)点M、N分别从点A、C同时出发、分别在射线AB、边BC的延长线上以相同的速度开始运动,动点M、N在运动过程中,DE的长会 (变小、变大、不变).
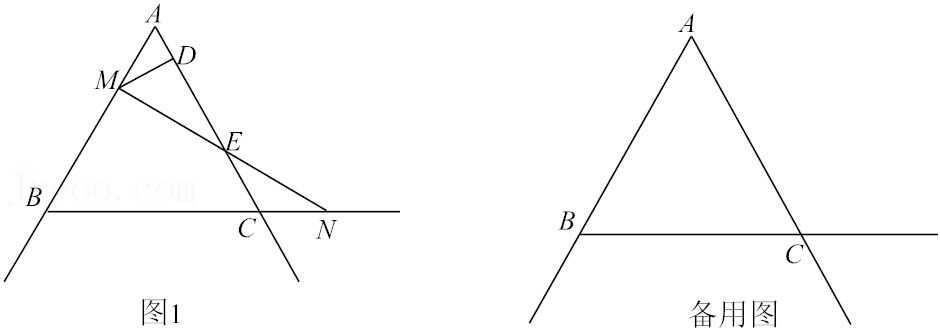
(1)如图1,当点M为AB的三等分点(靠近点A)时,DE的长为 .
(2)点M、N分别从点A、C同时出发、分别在射线AB、边BC的延长线上以相同的速度开始运动,动点M、N在运动过程中,DE的长会 (变小、变大、不变).
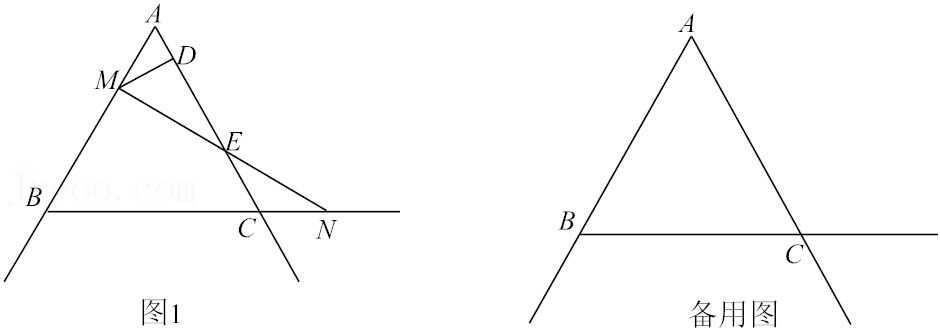
19.计算:
(1)4x2y•(-xy2)3;
(2)(x+2)(x-3).
(1)4x2y•(-xy2)3;
(2)(x+2)(x-3).
20.先化简,再求值:x2(x-1)-x(x2+x-1),其中x=
.
| 1 |
| 2 |
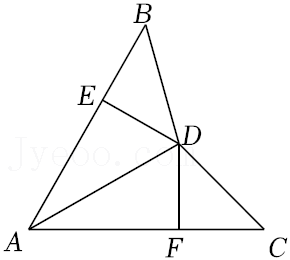
21.如图,AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F,求证:DE=DF.
证明:在△ABD和△ACD中,
,
∴△ABD≌△ACD( ),
∴∠ =∠ ( ),
∴AD是∠BAC的角平分线.
又∵DE⊥AB于E,DF⊥AC于F,
∴DE=DF( ).
证明:在△ABD和△ACD中,
| { |
|
∴△ABD≌△ACD( ),
∴∠ =∠ ( ),
∴AD是∠BAC的角平分线.
又∵DE⊥AB于E,DF⊥AC于F,
∴DE=DF( ).

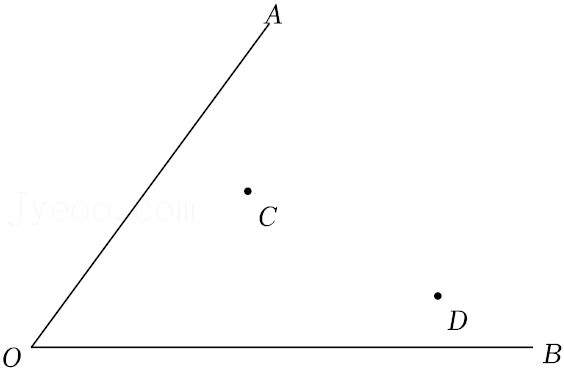
22.求作一点P,使P到∠AOB两边的距离相等,且PC=PD.(不写作法,保留作图痕迹)

23.如图,A、B、C、D四点共线,且AB=CD,CE⊥AB于C,DF⊥AB于D,请添加一个条件使△ACE≌△BDF,并证明.
添加条件: .
添加条件: .

24.如图,在△ABC中,AB⊥BC,DE是边AC的垂直平分线,连接AE.
(1)若∠C=20°,求∠BAE的度数.
(2)若∠C=30°,BE=4,求AE的长.
(1)若∠C=20°,求∠BAE的度数.
(2)若∠C=30°,BE=4,求AE的长.

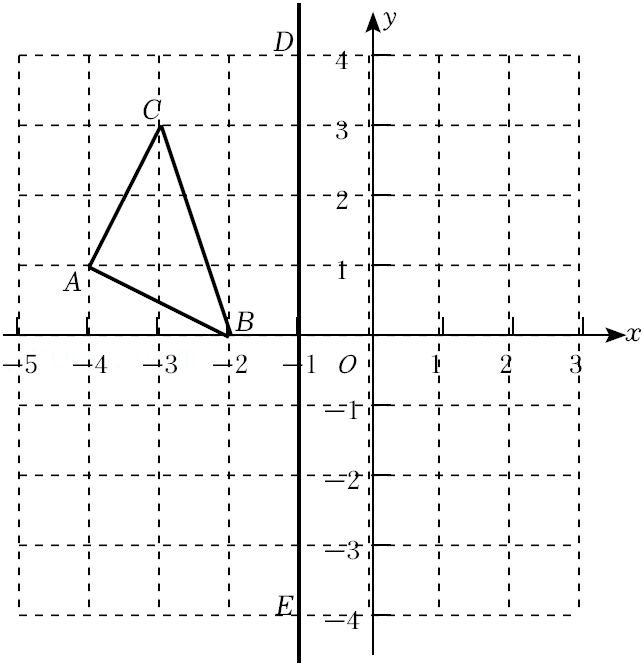
25.如图,在所给的平面直角坐标系中,完成下列各题(用直尺画图).
(1)若A(-4,1),C(-3,3),△A1B1C1与△ABC关于y轴成轴对称,直接写出△A1B1C1三个顶点坐标为A1 ,B1 ,C1 ;
(2)画出格点△ABC关于直线DE对称的△A2B2C2;
(3)在DE上画出点P,使PA+PC最小;
(4)在DE上画出点Q,使QA-QB最大.
(1)若A(-4,1),C(-3,3),△A1B1C1与△ABC关于y轴成轴对称,直接写出△A1B1C1三个顶点坐标为A1 ,B1 ,C1 ;
(2)画出格点△ABC关于直线DE对称的△A2B2C2;
(3)在DE上画出点P,使PA+PC最小;
(4)在DE上画出点Q,使QA-QB最大.

26.正方形是我们非常熟悉的几何图形,它是四条边都相等,四个角都是直角的正多边形,它是轴对称图形,有四条对称轴,正方形的一条对角线可以把它分成两个全等的等腰直角三角形(如图1),两条对角线可以把它分成四个全等的等腰直角三角形(如图2).
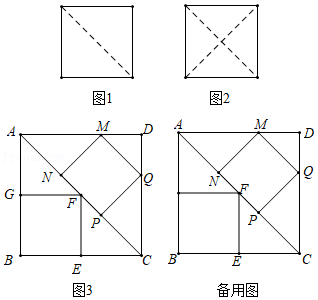
(1)图3中有三个正方形,正方形ABCD,正方形BEFG,正方形MNPQ,那么图中有 对全等的三角形.
(2)若正方形BEFG的面积为S1,正方形MNPQ的面积为S2,不通过计算,推测S1和S2的大小关系是 .
A.S1>S2ㅤㅤB.S1<S2ㅤㅤC.S1=S2
(3)若正方形ABCD的边长为18,则正方形BEFG的面积S1= ;正方形MNPQ的面积为S2= .
(4)若正方形MNPQ的面积S2=a,则正方形ABCD的面积S= .

(1)图3中有三个正方形,正方形ABCD,正方形BEFG,正方形MNPQ,那么图中有 对全等的三角形.
(2)若正方形BEFG的面积为S1,正方形MNPQ的面积为S2,不通过计算,推测S1和S2的大小关系是 .
A.S1>S2ㅤㅤB.S1<S2ㅤㅤC.S1=S2
(3)若正方形ABCD的边长为18,则正方形BEFG的面积S1= ;正方形MNPQ的面积为S2= .
(4)若正方形MNPQ的面积S2=a,则正方形ABCD的面积S= .
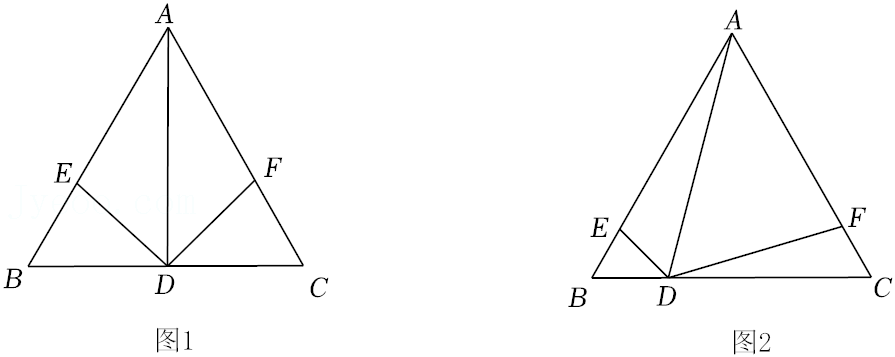
27.已知△ABC是等边三角形,点D是BC边上一动点(D不与B、C重合),连接AD,以AD为边作∠ADE=∠ADF,分别交AB,AC于点E,F.
(1)如图1,若点D是BC的中点,求证:AE=AF;
(2)如图2,若∠ADE=∠ADF=60°,猜测AE与AF的数量关系?并证明你的结论.
(1)如图1,若点D是BC的中点,求证:AE=AF;
(2)如图2,若∠ADE=∠ADF=60°,猜测AE与AF的数量关系?并证明你的结论.

28.对于平面直角坐标系内的任意两点P(x1,y1),Q(x2,y2),定义它们之间的“直角距离”为d(P,Q)=|x1-x2|+|y1-y2|.
对于平面直角坐标系内的任意两个图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的“直角距离”有最小值,那么称这个最小值为图形M,N间的“直角距离”,记作D(M,N).
(1)已知A(1,0),B(0,2),则d(A,B)= ,D(O,AB)= ;
(2)已知A(1,0),B(0,t),若D(O,AB)=1,则t的取值范围是 ;
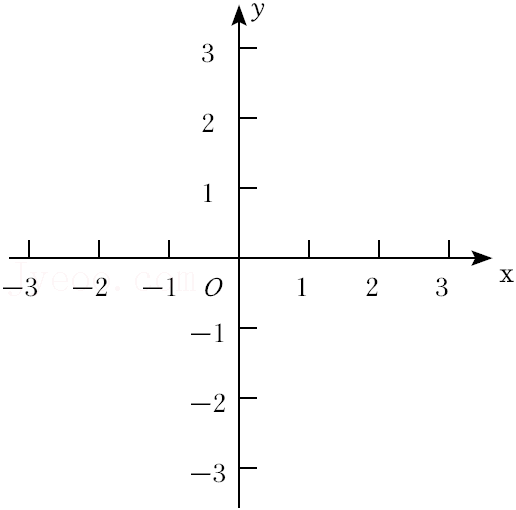
(3)已知A(1,0),若坐标平面内的点P满足d(P,A)=1,则在图中画出所有满足条件的点P所构成的图形,该图形的面积是 ;
(4)已知A(1,0),B(0,2),直线l过点(0,t)且垂直于y轴,若直线l上存在点Q满足d(Q,A)=d(Q,B),则t的取值范围是 .
对于平面直角坐标系内的任意两个图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的“直角距离”有最小值,那么称这个最小值为图形M,N间的“直角距离”,记作D(M,N).
(1)已知A(1,0),B(0,2),则d(A,B)= ,D(O,AB)= ;
(2)已知A(1,0),B(0,t),若D(O,AB)=1,则t的取值范围是 ;
(3)已知A(1,0),若坐标平面内的点P满足d(P,A)=1,则在图中画出所有满足条件的点P所构成的图形,该图形的面积是 ;
(4)已知A(1,0),B(0,2),直线l过点(0,t)且垂直于y轴,若直线l上存在点Q满足d(Q,A)=d(Q,B),则t的取值范围是 .






