试卷题目
1.下列图形都是由两个全等三角形组合而成,其中是轴对称图形的是( )
- A.

- B.

- C.

- D.

2.若如图中的两个三角形全等,图中的字母表示三角形的边长,则∠1的度数为( )
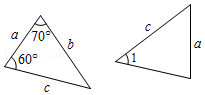

- A. 40°
- B. 50°
- C. 60°
- D. 70°
3.若x=-1,则下列分式的值为0的是( )
- A.
1 x-1 - B.
x x+1 - C.
x-1 x - D.
x2-1 x
4.下列各式中与
√3
是同类二次根式的是( )- A. √6
- B. √9
- C. √12
- D. √18
5.下列计算错误的是( )
- A. √(-3)2=3
- B. √3×√2=√6
- C. √3+√2=√5
- D. √6÷√3=√2
6.下列运算正确的是( )
- A. =x3
x6 x2 - B. =x+y
x2+y2 x+y - C. =
x+3 y+3 x y - D. =-1
-x+y x-y
7.以下列各组数为边长,不能构成直角三角形的是( )
- A. 5,12,13
- B. 1,2,√5
- C. 1,√3,2
- D. 4,5,6
8.如图所示在△ABC中,AB边上的高线画法正确的是( )
- A.

- B.

- C.

- D.

9.若
√x-3
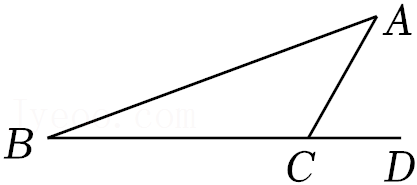
在实数范围内有意义,则x的取值范围是 .10.如图,△ABC中,∠B=20°,D是BC延长线上一点,且∠ACD=60°,则∠A的度数是 .

11.为庆祝建党100周年,某邮政局推出纪念封系列,且所有纪念封均采用形状、大小、质地都相同的卡片,背面分别印有“改革、开放、民族、复兴”的字样,正面完全相同.如下图,现将6张纪念封洗匀后正面向上放在桌子上,从中随机抽取一张,抽出的纪念封背面恰好印有“改革”字样的可能性大小是 .


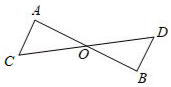
12.如图,线段AB,CD相交于点O,AO=BO,添加一个条件,能使△AOC≌△BOD,所添加的条件的是 .

13.等腰三角形一边长为5,另一边长为8,则其周长是 .
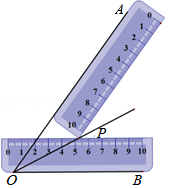
14.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是 .

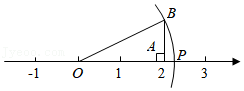
15.小丽同学在学习了利用勾股定理在数轴上表示无理数的方法后,进行如下操作:首先画数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,且AB=1;再以O为圆心,OB的长为半径作弧,交数轴正半轴于点P,如图,那么点P表示的数是 .

16.在△ABC中,∠C=90°,∠B=30°,BC=4,点D是边BC的中点,点E是边AB上的动点,点F是边AC上的动点,则DE+EF的最小值是 .
17.计算:
(1)
(2)2
(1)
√12
-3√27
+|-√3
|;(2)2
√20
×| 1 |
| 4 |
√5
÷4√5
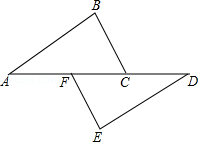
.18.已知:如图,点A,F,C,D在同一条直线上,点B和点E在直线AD的两侧,且AF=DC,BC//FE,∠A=∠D.
求证:AB=DE.
求证:AB=DE.

19.解方程:
+1=
.
| 2x |
| x+3 |
| 7 |
| 2x+6 |
20.计算:学习了分式运算后,老师布置了这样一道计算题:
-
,甲、乙两位同学的解答过程分别如下:
甲同学:
-
=
-
①
=
-
②
=
③
=
④
乙同学:
-
=
-
①
=
-
②
=2-(x+1)③
=1-x④
老师发现这两位同学的解答过程都有错误.
请你从甲、乙两位同学中,选择一位同学的解答过程,帮助他分析错因,并加以改正.
①我选择 同学的解答过程进行分析.(填“甲”或“乙” )
②该同学的解答从第 步开始出现错误(填序号),错误的原因是 ;
③请写出正确解答过程.
| 2 |
| x2-1 |
| 1 |
| x-1 |
甲同学:
| 2 |
| x2-1 |
| 1 |
| x-1 |
=
| 2 |
| (x+1)(x-1) |
| 1 |
| x-1 |
=
| 2 |
| (x+1)(x-1) |
| 1 |
| (x+1)(x-1) |
=
| 2-1 |
| (x+1)(x-1) |
=
| 1 |
| (x+1)(x-1) |
乙同学:
| 2 |
| x2-1 |
| 1 |
| x-1 |
=
| 2 |
| (x+1)(x-1) |
| 1 |
| x-1 |
=
| 2 |
| (x+1)(x-1) |
| x+1 |
| (x+1)(x-1) |
=2-(x+1)③
=1-x④
老师发现这两位同学的解答过程都有错误.
请你从甲、乙两位同学中,选择一位同学的解答过程,帮助他分析错因,并加以改正.
①我选择 同学的解答过程进行分析.(填“甲”或“乙” )
②该同学的解答从第 步开始出现错误(填序号),错误的原因是 ;
③请写出正确解答过程.
21.当x=
÷
-
的值.
√2
-1时,求代数式| 1 |
| x-2 |
| x+1 |
| x2-4x+4 |
| x-1 |
| x+1 |
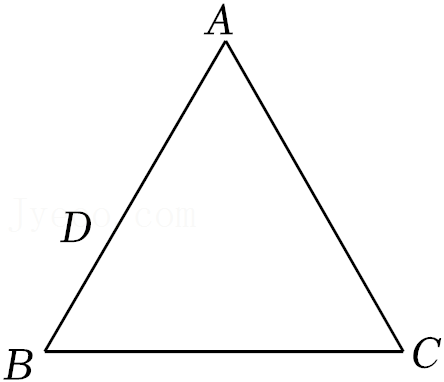
22.如图,点D是等边△ABC的边AB上一点,过点D作BC的平行线交AC于点E.
(1)依题意补全图形;
(2)判断△ADE的形状,并证明.
(1)依题意补全图形;
(2)判断△ADE的形状,并证明.

23.列方程解应用题:
第24届冬季奥林匹克运动会将于2025年2月4日至2月20日在中国北京和张家口市联合举行.北京冬奥会的配套设施“京张高铁” --北京至张家口高速铁路,已经全线通车,全长约175千米.原京张铁路是1909年由“中国铁路之父”詹天佑主持设计建造的中国第一条干线铁路,全长约210千米,用“人”字形铁轨铺筑的方式解决了火车上山的问题.京张高铁的平均速度是原京张铁路的5倍,可以提前5小时到达,求京张高铁的平均速度.
第24届冬季奥林匹克运动会将于2025年2月4日至2月20日在中国北京和张家口市联合举行.北京冬奥会的配套设施“京张高铁” --北京至张家口高速铁路,已经全线通车,全长约175千米.原京张铁路是1909年由“中国铁路之父”詹天佑主持设计建造的中国第一条干线铁路,全长约210千米,用“人”字形铁轨铺筑的方式解决了火车上山的问题.京张高铁的平均速度是原京张铁路的5倍,可以提前5小时到达,求京张高铁的平均速度.
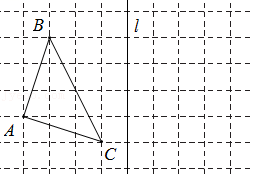
24.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,点A,B,C均落在格点上.
(1)计算线段AB的长度 ;
(2)判断△ABC的形状 ;
(3)写出△ABC的面积 ;
(4)画出△ABC关于直线l的轴对称图形△A1B1C1.
(1)计算线段AB的长度 ;
(2)判断△ABC的形状 ;
(3)写出△ABC的面积 ;
(4)画出△ABC关于直线l的轴对称图形△A1B1C1.

25.如图,△ABC中,∠ABC=45°,F是高AD和高BE的交点,AC=
求线段DF的长度.
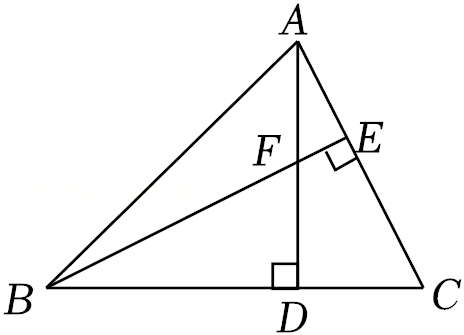
√5
,BD=2.求线段DF的长度.

26.尺规作图:
已知:如图1,直线MN和直线MN外一点P.
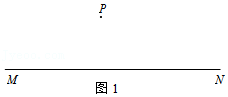
求作:直线PQ,使直线PQ//MN.
(1)使用直尺和圆规,按照小智的作图思路补全图形1(保留作图痕迹);
(2)完成下面的证明:
证明:∵AB平分∠PAN,
∴∠PAB=∠NAB.
∵PA=PQ,
∴∠PAB=∠PQA( ).
∴∠NAB=∠PQA.
∴PQ//MN( ).
(3)参考小智的作图思路和流程,另外设计一种作法,利用直尺和圆规在图2中完成.(温馨提示:保留作图痕迹,不用写作法和证明)
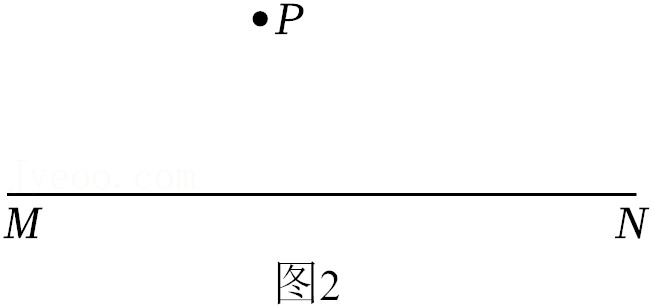
已知:如图1,直线MN和直线MN外一点P.

求作:直线PQ,使直线PQ//MN.
小智的作图思路如下:①如何得到两条直线平行?小智想到,自己学习线与角的时候,有4个定理可以证明两条直线平行,其中有“内错角相等,两条直线平行”.②如何得到两个角相等?小智先回顾了线与角的内容,找到了几个定理和1个概念,可以得到两个角相等.小智又回顾了三角形的知识,也发现了几个可以证明两个角相等的定理.最后,小智选择了角平分线的概念和“等边对等角”.③画出示意图: ④根据示意图,确定作图顺序. ④根据示意图,确定作图顺序. |
(1)使用直尺和圆规,按照小智的作图思路补全图形1(保留作图痕迹);
(2)完成下面的证明:
证明:∵AB平分∠PAN,
∴∠PAB=∠NAB.
∵PA=PQ,
∴∠PAB=∠PQA( ).
∴∠NAB=∠PQA.
∴PQ//MN( ).
(3)参考小智的作图思路和流程,另外设计一种作法,利用直尺和圆规在图2中完成.(温馨提示:保留作图痕迹,不用写作法和证明)

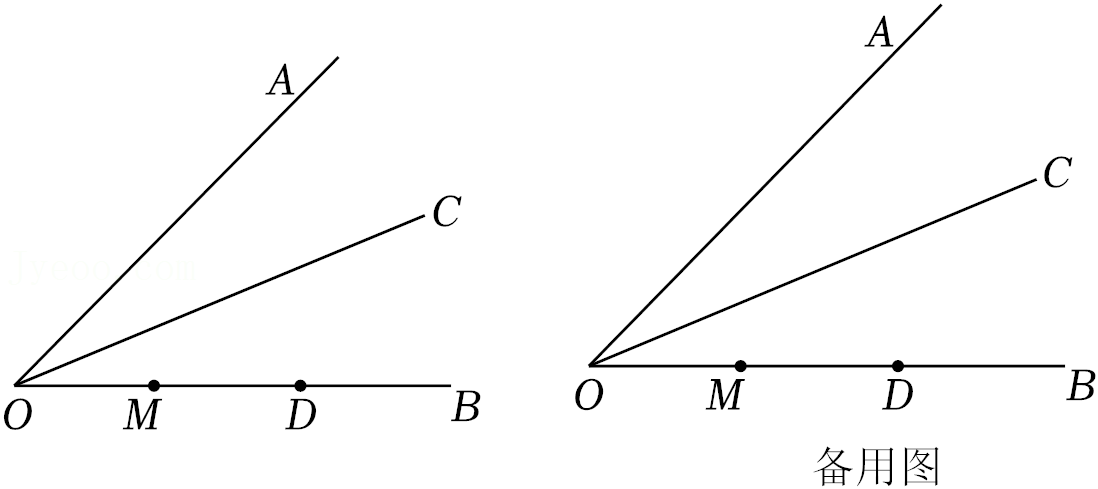
27.如图,∠AOB=45°,OC是∠AOB的角平分线,点D是射线OB上的一点,点M为线段OD的中点,过点M作OD的垂线,交射线OA于点E,交射线OC于点F,连接ED,交OC于点G.
(1)依题意补全图形;
(2)猜想EF和EG的数量关系并证明;
(3)求证:ED+EF=2EM.
(1)依题意补全图形;
(2)猜想EF和EG的数量关系并证明;
(3)求证:ED+EF=2EM.

热门排序
推荐文章
广东二模2025高三数学试题及答案解析
2020年陕西西安中考数学真题
2021-2025学年湖北省咸宁市咸安区七年级(上)期末数学试卷
2021-2025学年河南省濮阳市七年级(上)期末数学试卷(五四学制)
2021-2025学年河南省开封市七年级(上)期末数学试卷
2021-2025学年天津市和平区八年级(上)期末数学试卷
2021-2025学年山东省聊城市东昌府区八年级(上)期中数学试卷
2021-2025学年山东省烟台市高新区八年级(上)期中数学试卷(五四学制)
2021-2025学年广东省揭阳市揭东区八年级(上)期末数学试卷
2021-2025学年山东省潍坊市八年级(上)期中数学试卷





