试卷题目
1.函数y=
中,自变量x的取值范围是( )
| 1 |
√x-3 |
- A. x≠3
- B. x>3
- C. x≥3
- D. x≤3
2.下列二次根式中,最简二次根式是( )
- A. √
1 2 - B. √0.2
- C.
1 √2 - D. √2
2
3.下列计算正确的是( )
- A. √12-√3=√3
- B. √2+√3=√5
- C. 3√5×√5=4√5
- D. (2√2)2=4√2
4.如图,点A,B 都在格点上,点C在线段AB上,每个小格长度为1,若BC=
,则AC的长为( )
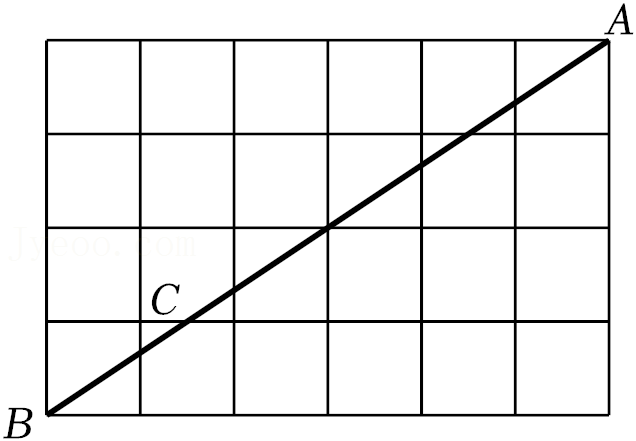
| 2 √13 |
| 3 |

- A. √13
- B.
4 √133 - C. 2√13
- D. 3√13
5.估计
的值应在( )之间.
√45 +√12 |
√3 |
- A. 3和4
- B. 4和5
- C. 5和6
- D. 6和7
6.如果方程(m-3)xm2-7-x+3=0是关于x的一元二次方程,那么m的值为( )
- A. ±3
- B. 3
- C. -3
- D. 都不对
7.根据下面表格中的对应值:
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
| 3.23 | 3.24 | 3.25 | 3.26 |
| -0.06 | -0.02 | 0.03 | 0.09 |
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
- A. 3<x<3.23
- B. 3.23<x<3.24
- C. 3.24<x<3.25
- D. 3.25<x<3.26
8.已知多项式P=
x-2,Q=x2-
x(x为任意实数),试比较多项式P与Q的大小( )
| 1 |
| 2 |
| 3 |
| 2 |
- A. 无法确定
- B. P>Q
- C. P=Q
- D. P<Q
9.已知关于x的一元二次方程x2+bx-1=0,则下列关于该方程根的判断,正确的是( )
- A. 有两个不相等的实数根
- B. 有两个相等的实数根
- C. 没有实数根
- D. 实数根的个数与实数b的取值有关
10.已知:
问题1,某厂用2年时间把总产值增加了原来的b倍,求每年平均增长的百分数;
问题2,总产值用2年的时间在原来a万元的基础上增加了b万元,求每年平均增长的百分数;
问题3,某厂用2年的时间把总产值增加到原来的b倍,求每年平均增长的百分数.
设每年平均增长的百分数x,那么下面的三个方程:①(1+x)2=b,②a(1+x)2=a+b,③(1+x)2=b+1,按问题1、2、3的序号排列,相对应的是( )
问题1,某厂用2年时间把总产值增加了原来的b倍,求每年平均增长的百分数;
问题2,总产值用2年的时间在原来a万元的基础上增加了b万元,求每年平均增长的百分数;
问题3,某厂用2年的时间把总产值增加到原来的b倍,求每年平均增长的百分数.
设每年平均增长的百分数x,那么下面的三个方程:①(1+x)2=b,②a(1+x)2=a+b,③(1+x)2=b+1,按问题1、2、3的序号排列,相对应的是( )
- A. ①②③
- B. ③②①
- C. ①③②
- D. ②①③
11.若关于x的一元二次方程ax2+bx+5=0(a≠0)有一根为2025,则方程a(x+1)2+b(x+1)=-5必有根为( )
- A. 2025
- B. 2020
- C. 2019
- D. 2021
12.对于一元二次方程ax2+bx+c=0(a≠0),下列说法:①若a+b+c=0,则b2-4ac≥0;②若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;③若c是方程ax2+bx+c=0的一个根,则一定有ac+b+1=0成立;④若x0是一元二次方程ax2+bx+c=0的根,则b2-4ac=(2ax0+b)2.其中正确的( )
- A. ①②
- B. ①②④
- C. ①②③④
- D. ①②③
13.
√(-9)2
= .14.关于x的一元二次方程x2+bx+c=0的两个实数根分别为2和-3,则分解因式:x2+bx+c= .
15.阅读理解:设
=(x1,y1),
=(x2,y2),若
⊥
,则
⋅
=0,即x1x2•+y1y2=0,已知
=(-2,x+1),
=(3,x+2),且
⊥
,则x的值为 .
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
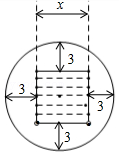
16.我国古代数学著作《增删算法统宗》记载“圆中方形”问题:“今有圆田一段,中间有个方池.丈量田地待耕犁,恰好三分在记,池面至周有数,每边三步无疑.内方圆径若能知,堪作算中第一.”其大意为:有一块圆形的田,中间有一块正方形水池,测量出除水池外圆内可耕地的面积恰好72平方步,从水池边到圆周,每边相距3步远.如果你能求出正方形边长和圆的直径,那么你的计算水平就是第一了.如图,设正方形的边长是x步,则列出的方程是 .

17.关于x的方程(k-1)x2+2kx+2=0,x1,x2是方程的两个根,设S=
+
+x1+x2,则当S的值为2时,k= .
| x2 |
| x1 |
| x1 |
| x2 |
18.计算:
(1)2
(2)(
(1)2
√12
-6√
+3| 1 |
| 3 |
√48
;(2)(
√5
+3)(√5
-3)-(√3
-1)2.19.在进行二次根式化简时,我们有时会遇到如
,
这样的式子,可以将其进一步化简:
=
=
;
=
=
以上这种化简的方法叫做分母有理化.
请化简下列各题(写出化简过程):
(1)
;
(2)
;
(3)
+
+
+⋯⋯+
.
| 5 |
√3 |
| 1 |
√6 -√2 |
| 5 |
√3 |
| 5× √3 |
√3 ×√3 |
| 5 √3 |
| 3 |
| 1 |
√6 -√2 |
√6 +√2 |
| ( √6 -√2 )(√6 +√2 ) |
√6 +√2 |
| 4 |
请化简下列各题(写出化简过程):
(1)
| 4 |
√15 +√7 |
(2)
| 1 |
| 5- √3 |
(3)
| 1 |
| 1+ √2 |
| 1 |
√2 +√3 |
| 1 |
√3 +√4 |
| 1 |
√49 +√50 |
20.如图,学校建一长方形自行车棚,一边靠墙(墙长18米),另三边用总长50米的栏杆围成,留2米宽的门,若想建成面积为240平方米的自行车棚,则车棚垂直于墙的一边的长为多少米?







