试卷题目
1.以下六个数:-
,3.14,
,
√2
,| π |
| 2 |
| 22 |
| 7 |
√64
,0.1010010001,无理数的个数是( )- A. 1
- B. 2
- C. 3
- D. 4
2.下列条件:①b2=c2-a2;②∠C=∠A-∠B;③a:b:c=
:
:
;④∠A:∠B:∠C=3:4:5,能判定△ABC是直角三角形的有( )
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
- A. 4个
- B. 3个
- C. 2个
- D. 1个
3.下列命题:①两点之间,直线最短;②角是轴对称图形,对称轴是它的角平分线;③同旁内角互补,两直线平行;④
√81
的平方根是±9,其中真命题的个数是( )- A. 1个
- B. 2个
- C. 3个
- D. 4个
4.若点P在x轴上方,y轴上的左边,到x轴的距离为3,到y轴的距离是4,则点P的坐标是( )
- A. (3,4)
- B. (4,3)
- C. (3,-4)
- D. (-4,3)
5.如图,AB∥CD,BF交CD于点E,AE⊥BF,∠CEF=34°,则∠A的度数是( )
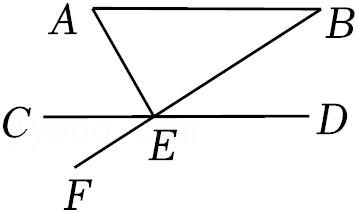

- A. 34°
- B. 66°
- C. 56°
- D. 46°
6.八(3)班七个兴趣小组人数分别为4、4、5、x、6、6、7,已知这组数据的平均数是5,则这组数据的中位数是( )
- A. 6
- B. 5
- C. 4
- D. 3
7.已知方程组
的解满足x+y=1,则k的值为( )
| { |
|
- A. 7
- B. -7
- C. 1
- D. -1
8.已知(k,b)为第四象限内的点,则一次函数y=kx-b的图象大致是( )
- A.

- B.

- C.

- D.

9.在沙县国际连锁早餐店里,李大爷买5个馒头、3个包子,老板少拿2元,只要17元;张大妈买11个馒头、5个包子,老板以售价的九折优惠,只要33.3元.若馒头每个x元,包子每个y元,依题意可列方程组为( )
- A.
{ 5x+3y=17+2 11x+5y=33.3×0.9 - B.
{ 5x+3y=17+2 11x+5y=33.3÷0.9 - C.
{ 5x+3y=17-2 11x+5y=33.3×0.9 - D.
{ 5x+3y=17-2 11x+5y=33.3÷0.9
10.如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A对应点为A′,且B′C=3,则AM的长是( )
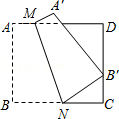

- A. 1.5
- B. 2
- C. 2.25
- D. 2.5
11.若直角三角形两边分别是3和4,则第三边是 .
12.新兴农场果农随机从甲、乙、丙三个品种的枇杷树中各选10棵,每棵产量的平均数x(单位:千克)及方差(单位:千克2)如下表所示,他准备从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是 .
| 甲 | 乙 | 丙 | |
| x | 44 | 44 | 42 |
| S2 | 1.7 | 1.5 | 1.7 |
13.一次函数y=kx+b与y=x-2的图象如图所示,则关于x、y的方程组
的解是 .
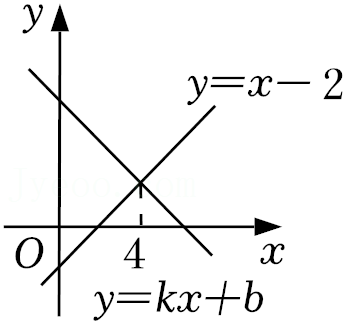
| { |
|

14.元旦期间,大兴商场搞优惠活动,其活动内容是:凡在本商场一次性购买商品超过100元者,超过100元的部分按8折优惠.在此活动中,小明到该商场一次性购买单价为60元的礼盒x(x>2)件,则应付款y(元)与商品数x(件)之间的关系式,化简后的结果是 .
15.如图,平面直角坐标系中,直线y=
x+1与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD,在y轴上有一个动点M,当△MDC的周长最小的时候,点M的坐标是 .
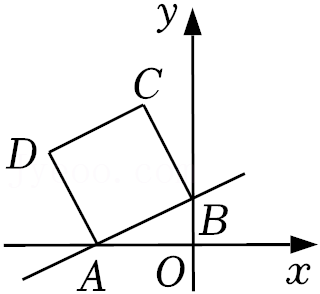
| 1 |
| 2 |

16.(1)计算:
-(
(2)解方程组
.
√27 +√12 |
√3 |
√2
-√3
)2-|-√6
|;(2)解方程组
| { |
|
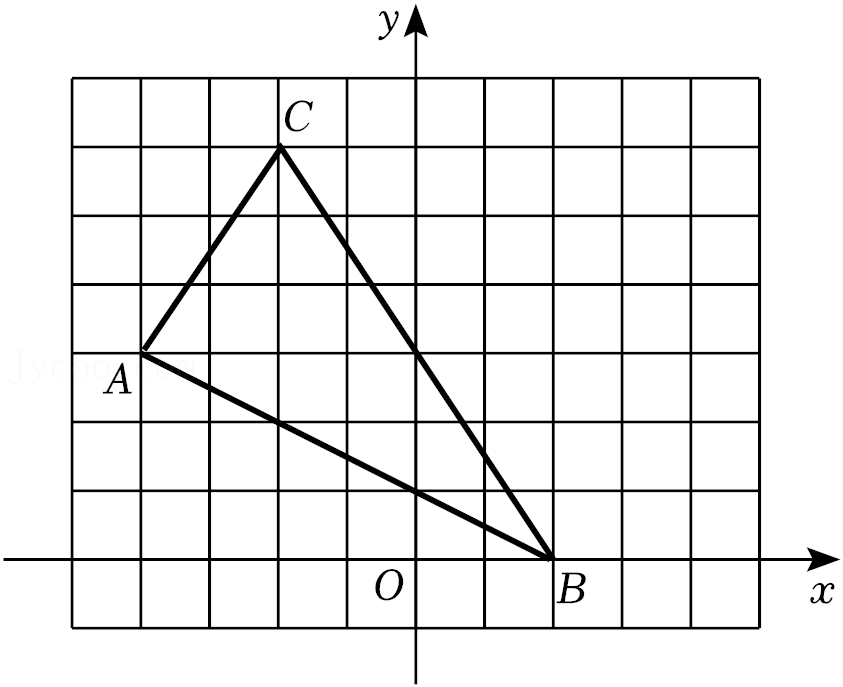
17.如图,平面直角坐标系中,△ABC的顶点都在格点上,已知点A的坐标是(-4,3).
(1)点B的坐标是 ;
(2)画出△ABC关于y轴对称的△A′B′C′,其中点A、B、C的对应点分别为点A′、B′、C′;
(3)直接写出△ABC的面积为 .
(1)点B的坐标是 ;
(2)画出△ABC关于y轴对称的△A′B′C′,其中点A、B、C的对应点分别为点A′、B′、C′;
(3)直接写出△ABC的面积为 .

18.为响应“双减”政策,老师们都精心设计每天的作业,兴华学校调查了部分学生每天完成作业所用时间,并用得到的数据绘制了如下不完整的统计图,根据图中信息完成下列问题:
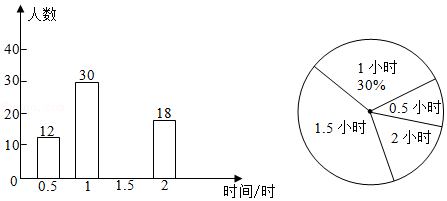
(1)将条形统计图补充完整;
(2)抽查学生完成作业所用时间的众数是 ;
(3)求所有被抽查学生完成作业所用的平均时间.

(1)将条形统计图补充完整;
(2)抽查学生完成作业所用时间的众数是 ;
(3)求所有被抽查学生完成作业所用的平均时间.
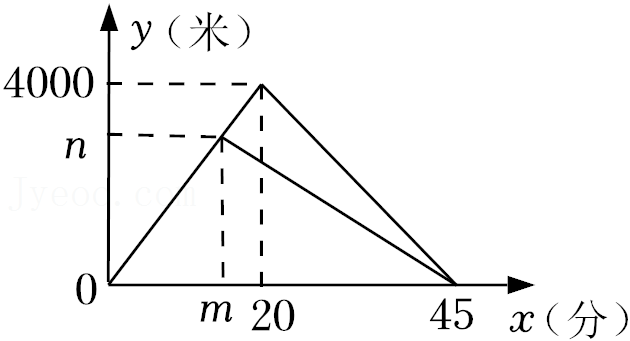
19.张明和爸爸一起出去跑步,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,张明继续前行,5分钟后也原路返回,两人恰好同时到家.张明和爸爸在整个过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示.
(1)n的值为 ;
(2)张明开始返回时与爸爸相距 米;
(3)第 分钟时,两人相距900米.
(1)n的值为 ;
(2)张明开始返回时与爸爸相距 米;
(3)第 分钟时,两人相距900米.

20.已知:如图,△ABC中,点D、E分别在AB、AC上,EF交DC于点F,∠3+∠2=180°,∠1=∠B.
(1)求证:DE∥BC;
(2)若DE平分∠ADC,∠3=3∠B,求∠2的度数.

(1)求证:DE∥BC;
(2)若DE平分∠ADC,∠3=3∠B,求∠2的度数.

21.五和超市购进A、B两种饮料共200箱,两种饮料的成本与销售价如下表:
(1)若该超市花了6500元进货,求购进A、B两种饮料各多少箱?
(2)设购进A种饮料a箱(50≤a≤100),200箱饮料全部卖完可获利润W元,求W与a的函数关系式,并求购进A种饮料多少箱时,可获得最大利润,最大利润是多少?
| 饮料 | 成本(元/箱) | 销售价(元/箱) |
| A | 25 | 35 |
| B | 35 | 50 |
(1)若该超市花了6500元进货,求购进A、B两种饮料各多少箱?
(2)设购进A种饮料a箱(50≤a≤100),200箱饮料全部卖完可获利润W元,求W与a的函数关系式,并求购进A种饮料多少箱时,可获得最大利润,最大利润是多少?
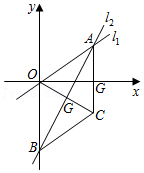
22.如图,在平面直角坐标系中,直线l1:y=
x与直线l2:y=kx+b相交于点A(a,3),直线交l2交y轴于点B(0,-5)
(1)求直线l2的解析式;
(2)将△OAB沿直线l2翻折得到△CAB(其中点O的对应点为点C),求证AC∥OB;
(3)在直线BC下方以BC为边作等腰直角三角形BCP,直接写出点P的坐标.
| 3 |
| 4 |
(1)求直线l2的解析式;
(2)将△OAB沿直线l2翻折得到△CAB(其中点O的对应点为点C),求证AC∥OB;
(3)在直线BC下方以BC为边作等腰直角三角形BCP,直接写出点P的坐标.






