试卷题目
1．若一个三角形的两边长分别为3和7，则第三边长可能是( )
- A. 2
- B. 3
- C. 4
- D. 5
2．要使分式
有意义，则x应满足的条件是( )
| 1 |
| x+1 |
- A. x≠1
- B. x≠-1
- C. x≠0
- D. x＞1
3．在
，-2ab2，
，
中，分式共有( )
| b |
| a |
| x |
| 3 |
| 1 |
| 4+x |
- A. 2个
- B. 3个
- C. 4个
- D. 5个
4．若(ambn)3=a9b15，则m、n的值分别为( )
- A. 9；5
- B. 3；5
- C. 5；3
- D. 6；12
5．等腰三角形的一个角是50°，则它的底角是( )
- A. 50°
- B. 50°或65°
- C. 80°或50°
- D. 65°
6．为加快“最美毕节”环境建设，某园林公司增加了人力进行大型树木移植，现在平均每天比原计划多植树30棵，现在植树400棵所需时间与原计划植树300棵所需时间相同，设现在平均每天植树x棵，则列出的方程为( )
- A. =
400 x 300 x-30 - B. =
400 x-30 300 x - C. =
400 x+30 300 x - D. =
400 x 300 x+30
7．如图，两个三角形为全等三角形，则∠α的度数是( )
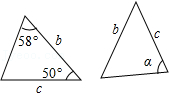
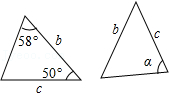
- A. 72°
- B. 60°
- C. 58°
- D. 50°
8．计算
-
的结果是( )
| 1 |
| x |
| 1 |
| x-y |
- A. -
y x(x-y) - B.
2x+y x(x-y) - C.
2x-y x(x-y) - D.
y x(x-y)
9．如图，△ABC中，AB=AC，AB的垂直平分线交AC于P点，若AB=5cm，BC=3cm，则△PBC的周长等于( )
- A. 4cm
- B. 6cm
- C. 8cm
- D. 10cm
10．计算-(-2x3y2)4的结果是( )
- A. 16x7y6
- B. -16x7y6
- C. 16x12y8
- D. -16x12y8
11．当x= 时，分式
没有意义．
| x2-4 |
| x-2 |
12．填空：(a-3)4= ．
13．定理“线段垂直平分线上的点到线段两端的距离相等”的逆定理是： ．
14．如图，在△ABC中，∠A=45°，∠B=60°，则外角∠ACD= 度．
15．已知一个等腰三角形的两边长分别为2和4，则该等腰三角形的周长是 ．
16．肥皂泡的泡壁厚度大约是0.0007mm，将0.0007用科学记数法表示为 ．
17．已知
-
=
，则
的值是 ．
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| ab |
| a-b |
18．化简：
÷
= ．
| a2-1 |
| a2+2a+1 |
| a2-a |
| a+1 |
19．一副透明的三角板，如图叠放，直角三角板的斜边AB、CE相交于点D，则∠BDC= ．
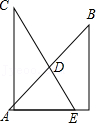
20．当m= 时，方程
=2-
会产生增根．
| x |
| x-3 |
| m |
| x-3 |
21．计算：
(1)a-2b-2•(-3a2b3)2．
(2)
=
．
(1)a-2b-2•(-3a2b3)2．
(2)
| 100 |
| x |
| 30 |
| x+7 |
22．先化简，再求值：(1-
)•
，其中x=2．
| 2 |
| x-1 |
| x2-x |
| x2-6x+9 |
23．如图，在△ABC中，AD⊥BC，AB=AC，∠BAD=18°，且AD=AE，求∠EDC的度数．
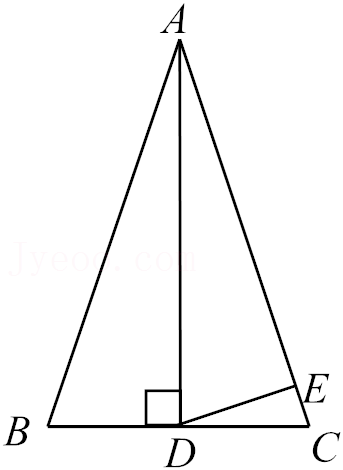
24．如图，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别为D，E．
求证：△ACD≌△CBE．
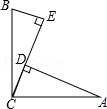
求证：△ACD≌△CBE．
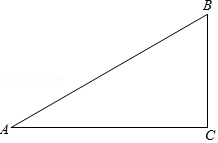
25．已知：如图，在△ABC中，∠A=30°，∠B=60°．
(1)作∠B的平分线BD，交AC于点D；作AB的中点E(要求：尺规作图，保留作图痕迹，不必写作法和证明)；
(2)连接DE，求证：△ADE≌△BDE．
(1)作∠B的平分线BD，交AC于点D；作AB的中点E(要求：尺规作图，保留作图痕迹，不必写作法和证明)；
(2)连接DE，求证：△ADE≌△BDE．
26．甲、乙两座城市的中心火车站A，B两站相距360km．一列动车与一列特快列车分别从A，B两站同时出发相向而行，动车的平均速度比特快列车快54km/h，当动车到达B站时，特快列车恰好到达距离A站135km处的C站．求动车和特快列车的平均速度各是多少？
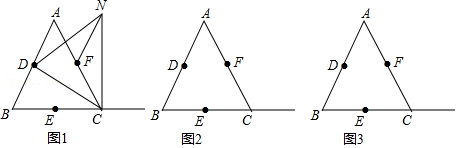
27．已知△ABC是等边三角形，点D，E，F分别是边AB，BC，AC的中点，点M是射线EC上的一个动点，作等边△DMN，使△DMN与△ABC在BC边同侧，连接NF．
(1)如图1，当点M与点C重合时，直接写出线段FN与线段EM的数量关系；
(2)当点M在线段EC上(点M与点E，C不重合)时，在图2中依题意补全图形，并判断(1)中的结论是否成立？若成立，请证明；若不成立，请说明理由；
(3)连接DF，直线DM与直线AC相交于点G，若△DNF的面积是△GMC面积的9倍，AB=8，请直接写出线段CM的长．
(1)如图1，当点M与点C重合时，直接写出线段FN与线段EM的数量关系；
(2)当点M在线段EC上(点M与点E，C不重合)时，在图2中依题意补全图形，并判断(1)中的结论是否成立？若成立，请证明；若不成立，请说明理由；
(3)连接DF，直线DM与直线AC相交于点G，若△DNF的面积是△GMC面积的9倍，AB=8，请直接写出线段CM的长．
