试卷题目
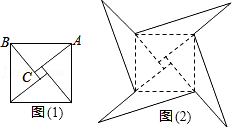
1．图中是轴对称图形的是( )
- A.
- B.
- C.
- D.
2．正多边形的一个内角等于144°，则该多边形是正( )边形．
- A. 8
- B. 9
- C. 10
- D. 11
3．下列命题中，真命题的个数是( )
①全等三角形的周长相等
②全等三角形的对应角相等
③全等三角形的面积相等
④面积相等的两个三角形全等．
①全等三角形的周长相等
②全等三角形的对应角相等
③全等三角形的面积相等
④面积相等的两个三角形全等．
- A. 4
- B. 3
- C. 2
- D. 1
4．如图，△ABC与△A′B′C′关于直线l对称，则∠B的度数为( )
- A. 30°
- B. 50°
- C. 90°
- D. 100°
5．如图，△ABC≌△ADE，∠B=80°，∠C=30°，∠DAC=35°，则∠EAC的度数为( )
- A. 40°
- B. 35°
- C. 30°
- D. 25°
6．在△ABC和△A′B′C′中，已知∠A=∠A′，AB=A′B′，添加下列条件中的一个，不能使△ABC≌△A′B′C′一定成立的是( )
- A. AC=A′C′
- B. BC=B′C′
- C. ∠B=∠B′
- D. ∠C=∠C′
7．长为l的一根绳，恰好可围成两个全等三角形(无公共边)，则其中一个三角形的最长边x的取值范围为( )
- A. ≤x＜
l 6 l 4 - B. ≤x＜
l 8 l 4 - C. ＜x＜
l 6 l 4 - D. ＜x＜
l 8 l 4
8．如图是一个等边三角形木框，甲虫P在边框AC上爬行(A，C端点除外)，设甲虫P到另外两边的距离之和为d，等边三角形ABC的高为h，则d与h的大小关系是( )
- A. d＞h
- B. d＜h
- C. d=h
- D. 无法确定
9．如图，在△ABC中，AD是它的角平分线，AB=8cm，AC=6cm，则S△ABD：S△ACD=( )
- A. 3：4
- B. 4：3
- C. 16：9
- D. 9：16
10．如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E、F，给出以下四个结论：
①△PFA≌△PEB；
②∠PFE=45°；
③EF=AP；
④图中阴影部分的面积是△ABC的面积的一半；
当∠EPF在△ABC内绕顶点P旋转时(点E不与A，B重合)，上述结论中始终正确的有( )
①△PFA≌△PEB；
②∠PFE=45°；
③EF=AP；
④图中阴影部分的面积是△ABC的面积的一半；
当∠EPF在△ABC内绕顶点P旋转时(点E不与A，B重合)，上述结论中始终正确的有( )
- A. 1个
- B. 2个
- C. 3个
- D. 4个
11．在△ABC中，∠A-∠B=30°，∠C=4∠B，则∠A= ，∠B= ，∠C= ．
12．若P关于x轴的对称点为P1(2a+b，-a+1)，关于y轴对称的点为P2(4-b，b+2)，则P点的坐标为 ．
13．如图所示，有一块三角形田地，AB=AC=10m，作AB的垂直平分线ED交AC于D，交AB于E，量得△BDC的周长为17m，请你替测量人员计算BC的长是 ．
14．如图，如图△ABE≌△DCE，AE=2cm，BE=1.2cm，∠A=25°，∠B=48°，那么DE= cm，∠C= °．
15．如图，AC、BD相交于点O，∠A=∠D，请补充一个条件，使△AOB≌△DOC，你补充的条件是 (填出一个即可)．
16．如图，△ABC是等腰直角三角形，∠C=90°，BD平分∠CBA交AC于点D，DE⊥AB于E．若△ADE的周长为8cm，则AB= cm．
17．如图，已知D是等边△ABC内一点，DB=DA，BE=BA，∠DBE=∠DBC，则∠BED= ．
18．如图，在Rt△ABC中，∠ACB=90°，∠B=30°，BC=8，AD平分∠CAB交BC于D点，E，F分别是AD，AC上的动点，则EC+EF的最小值为 ．
19．画出△ABC关于直线L的对称图形△A′B′C′．
20．如图，在△ABC中，AC=6，BC=8，AD⊥BC于D，AD=5，BE⊥AC于E，求BE的长．
21．如图，在△ABC中，∠B=63°，∠C=51°，AD是BC边上的高，AE是∠BAC的平分线，求∠DAE的度数．
22．已知：如图，点A、D、C在同一直线上，AB∥EC，AC=CE，∠B=∠EDC．求证：BC=DE．
23．如图，△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求∠DFB和∠DGB的度数．
24．已知：如图，AC=BD，AD⊥AC，BC⊥BD．求证：AD=BC．
25．已知：如图，Rt△ABC中，∠BAC=90°．
(1)按要求作图：(保留作图痕迹)
①延长BC到点D，使CD=BC；
②延长CA到点E，使AE=2CA；
③连接AD，BE并猜想线段 AD与BE的大小关系；
(2)证明(1)中你对线段AD与BE大小关系的猜想．
(1)按要求作图：(保留作图痕迹)
①延长BC到点D，使CD=BC；
②延长CA到点E，使AE=2CA；
③连接AD，BE并猜想线段 AD与BE的大小关系；
(2)证明(1)中你对线段AD与BE大小关系的猜想．
26．如图1，在△ABC中，∠ACB为锐角．点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．
解答下列问题：
(1)如果AB=AC，∠BAC=90°．
①当点D在线段BC上时(与点B不重合)，如图2，线段CF、BD之间的位置关系为 ，数量关系为 ．
②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，为什么？
(2)如果AB≠AC，∠BAC≠90°，点D在线段BC上运动．试探究：当△ABC满足一个什么条件时，CF⊥BC(点C、F重合除外)？画出相应图形，并说明理由．(画图不写作法)
解答下列问题：
(1)如果AB=AC，∠BAC=90°．
①当点D在线段BC上时(与点B不重合)，如图2，线段CF、BD之间的位置关系为 ，数量关系为 ．
②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，为什么？
(2)如果AB≠AC，∠BAC≠90°，点D在线段BC上运动．试探究：当△ABC满足一个什么条件时，CF⊥BC(点C、F重合除外)？画出相应图形，并说明理由．(画图不写作法)
热门排序
推荐文章
广东二模2023高三数学试题及答案解析
2021-2022学年四川省广元市朝天区八年级（上）期末数学试卷
2021-2022学年广东省汕头市潮阳区八年级（上）期中数学试卷
2021-2022学年广东省东莞市八年级（上）期中数学试卷
2020年内蒙古呼伦贝尔中考数学真题
2021-2022学年山东省威海市文登区八年级（上）期中数学试卷（五四学制）
2021-2022学年湖北省黄冈市八年级（上）期中数学试卷
2021-2022学年湖北省黄冈市八年级（下）期中数学试卷
2021-2022学年河北省唐山市路北区八年级（上）期末数学试卷
2021-2022学年山东省泰安市泰山区八年级（上）期中数学试卷（五四学制）
