试卷题目
1．剪纸是我国最古老的民间艺术之一，被列入第四批《人类非物质文化遗产代表作名录》，下列剪纸作品中，是轴对称图形的为( )
- A.
- B.
- C.
- D.
2．下列运算正确的是( )
- A. a2•a5=a10
- B. a2+a2=a4
- C. (a2b)3=a5b3
- D. (-a2)4=a8
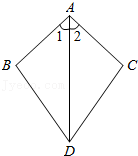
3．如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是( )
- A. AB=AC
- B. BD=CD
- C. ∠B=∠C
- D. ∠BDA=∠CDA
4．在平面直角坐标系xOy中，点P(-3，5)关于x轴的对称点的坐标是( )
- A. (3，5)
- B. (3，-5)
- C. (5，-3)
- D. (-3，-5)
5．如图，△ABC≌△DCB，若AC=7，BE=5，则DE的长为( )
- A. 2
- B. 3
- C. 4
- D. 5
6．下列命题中正确的有( )个
①三个内角对应相等的两个三角形全等；
②三条边对应相等的两个三角形全等；
③有两角和一边分别对应相等的两个三角形全等；
④等底等高的两个三角形全等．
①三个内角对应相等的两个三角形全等；
②三条边对应相等的两个三角形全等；
③有两角和一边分别对应相等的两个三角形全等；
④等底等高的两个三角形全等．
- A. 1
- B. 2
- C. 3
- D. 4
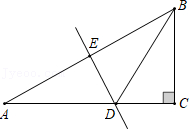
7．如图，在Rt△ABC中，∠A=30°，DE垂直平分AB，垂足为点E，交AC于D点，连接BD，若DE=2，则AC的值为( )
- A. 4
- B. 6
- C. 8
- D. 10
8．下面四个整式中，不能表示图中阴影部分面积的是( )
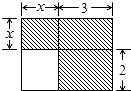
- A. (x+3)(x+2)-2x
- B. x(x+3)+6
- C. 3(x+2)+x2
- D. x2+5x
9．已知，如图在直角坐标系中，点A在y轴上，BC⊥x轴于点C，点A关于直线OB的对称点D恰好在BC上，点E与点O关于直线BC对称，∠OBC=35°，则∠OED的度数为( )
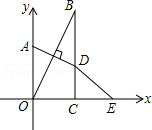
- A. 10°
- B. 20°
- C. 30°
- D. 35°
10．如图所示，在长方形ABCD的对称轴l上找点P，使得△PAB，△PBC，△PDC，△PAD均为等腰三角形，则满足条件的点P有( )
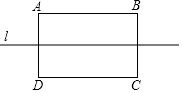
- A. 5个
- B. 4个
- C. 3个
- D. 1个
11．计算
a2•(-6ab)的结果是 ．
| 1 |
| 3 |
12．如图，已知OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点．若PA=2，则PQ的最小值为 ，理论根据为 ．
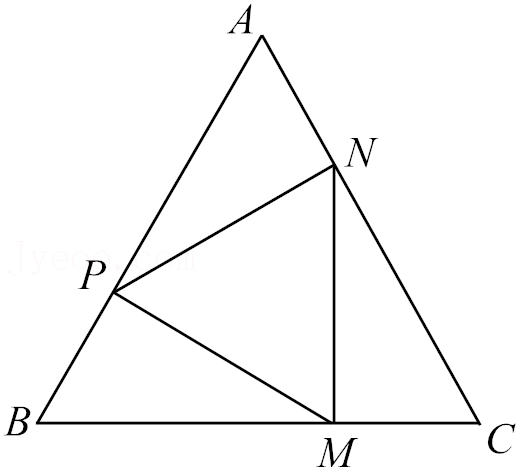
13．如图，点P、M、N分别在等边三角形ABC的各边上，且MP⊥AB于点P，MN⊥BC于点M，PN⊥AC于点N，若AB=15cm，则CM的长为 ．
14．若等腰三角形的一个外角为140°，则它的顶角的度数为 ．
15．已知a=8131，b=2741，c=961，则a、b、c的大小关系是 ．
16．如图，Rt△ABC中，∠ACB=90°，AC=6，BC=8，AB=10，BD平分∠ABC，如果M、N分别为BD、BC上的动点，那么CM+MN的最小值是 ．
17．如果xn=y，那么我们规定(x，y)=n．例如：因为32=9，所以(3，9)=2．
根据上述规定，(2，8)= ，若(m，16)=p，(m，5)=q，(m，t)=r，且满足p+q=r，则t= ．
根据上述规定，(2，8)= ，若(m，16)=p，(m，5)=q，(m，t)=r，且满足p+q=r，则t= ．
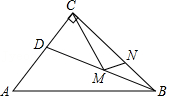
18．如图，点D是△ABC三条角平分线的交点，∠ABC=68°，若AB+BD=AC，则∠ACB的度数为 ．
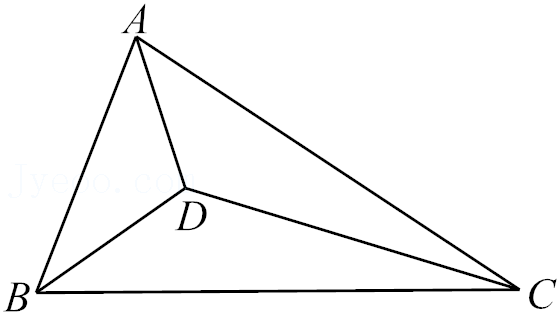
19．计算：
(1)a•(a2)3•(-a2)；
(2)4xy2•(
x2yz3)；
(3)2xy(x2-3y2)-4xy(2x2+y2)；
(4)(3x-2)(x+5)．
(1)a•(a2)3•(-a2)；
(2)4xy2•(
| 3 |
| 8 |
(3)2xy(x2-3y2)-4xy(2x2+y2)；
(4)(3x-2)(x+5)．
20．先化简，再求值．x(2x2-4x)-x2(6x-3)+x(2x)2，其中x=-
．
| 1 |
| 2 |
21．下面是小芸设计的“作三角形一边上的高”的尺规作图过程．
已知：△ABC．
求作：△ABC的边BC上的高AD．
作法：①以点A为圆心，适当长为半径画弧，交直线BC于点M，N；
②分别以点M，N为圆心，以大于
MN的长为半径画弧，两弧相交于点P；
③作直线AP交BC于点D，则线段AD即为所求△ABC的边BC上的高．
根据小芸设计的尺规作图过程：
(1)使用直尺和圆规，补全图形；(保留作图痕迹)
(2)AP是线段MN的 ．(填下列选项的序号)
①垂直平分线
②角平分线
点P在这条线上的依据是 ．
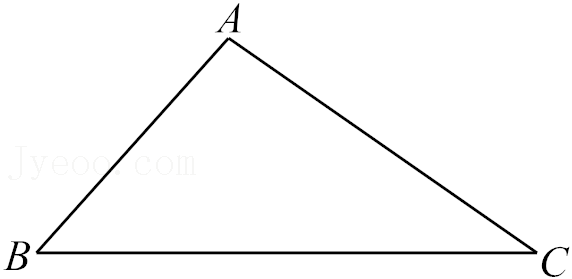
已知：△ABC．
求作：△ABC的边BC上的高AD．
作法：①以点A为圆心，适当长为半径画弧，交直线BC于点M，N；
②分别以点M，N为圆心，以大于
| 1 |
| 2 |
③作直线AP交BC于点D，则线段AD即为所求△ABC的边BC上的高．
根据小芸设计的尺规作图过程：
(1)使用直尺和圆规，补全图形；(保留作图痕迹)
(2)AP是线段MN的 ．(填下列选项的序号)
①垂直平分线
②角平分线
点P在这条线上的依据是 ．
22．如图，△ABC中，AB=AC，∠B=30°，点D是AC的中点，过点D作DE⊥AC交BC于点E，连接AE．若AE=3，求BC的长．
解：∵AB=AC，∠B=30°．
∴∠C=∠B=30°( )，
∴∠BAC=180°-∠B-∠C=120°．
∵点D是AC的中点，且DE⊥AC，
∴EC=EA=3( )，
∴∠EAC=∠C=30°，
∴∠BAE=∠BAC-∠EAC= °．
∵在Rt△ABE中，∠B=30°，
∴BE=2 = ，
∴BC=BE+EC= ．
解：∵AB=AC，∠B=30°．
∴∠C=∠B=30°( )，
∴∠BAC=180°-∠B-∠C=120°．
∵点D是AC的中点，且DE⊥AC，
∴EC=EA=3( )，
∴∠EAC=∠C=30°，
∴∠BAE=∠BAC-∠EAC= °．
∵在Rt△ABE中，∠B=30°，
∴BE=2 = ，
∴BC=BE+EC= ．
23．已知：如图，∠BAC=∠DAM，AB=AN，AD=AM，求证：∠B=∠ANM．
24．如图，已知∠A=∠D=90°，AB=DC，AC与BD相交于E，F是BC的中点，求证：∠BEF=∠CEF．
25．已知：如图，D是△ABC的边BA延长线上一点，且AD=AB，E是边AC上一点，且DE=BC．求证：∠DEA=∠C．
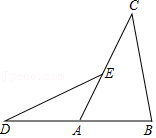
26．在平面直角坐标系xOy中，点A(t-1，1)与点B关于过点(t，0)且垂直于x轴的直线对称．
(1)以AB为底边作等腰三角形ABC，
①当t=2时，点B的坐标为 ；
②当t=0.5且直线AC经过原点O时，点C与x轴的距离为 ；
③若△ABC上所有点到y轴的距离都不小于1，则t的取值范围是 ．
(2)以AB为斜边作等腰直角三角形ABD，直线m过点(0，b)且与x轴平行，若直线m上存在点P，△ABD上存在点K，满足PK=1，直接写出b的取值范围．
(1)以AB为底边作等腰三角形ABC，
①当t=2时，点B的坐标为 ；
②当t=0.5且直线AC经过原点O时，点C与x轴的距离为 ；
③若△ABC上所有点到y轴的距离都不小于1，则t的取值范围是 ．
(2)以AB为斜边作等腰直角三角形ABD，直线m过点(0，b)且与x轴平行，若直线m上存在点P，△ABD上存在点K，满足PK=1，直接写出b的取值范围．
27．在等边△ABC中，线段AM为BC边上的中线．点D在直线AM上，以CD为一边在CD的下方作等边△CDE，连接BE．
(1)当点D在线段AM上时，
①请在图1中补全图形；
②∠CAM的度数为 ；
③求证：△ADC≌△BEC；
(2)当点D在直线AM上时，直线BE与直线AM的交点为O(点D与点M不重合，点E与点O不重合)，直接写出线段OE，OM与OD的数量关系．
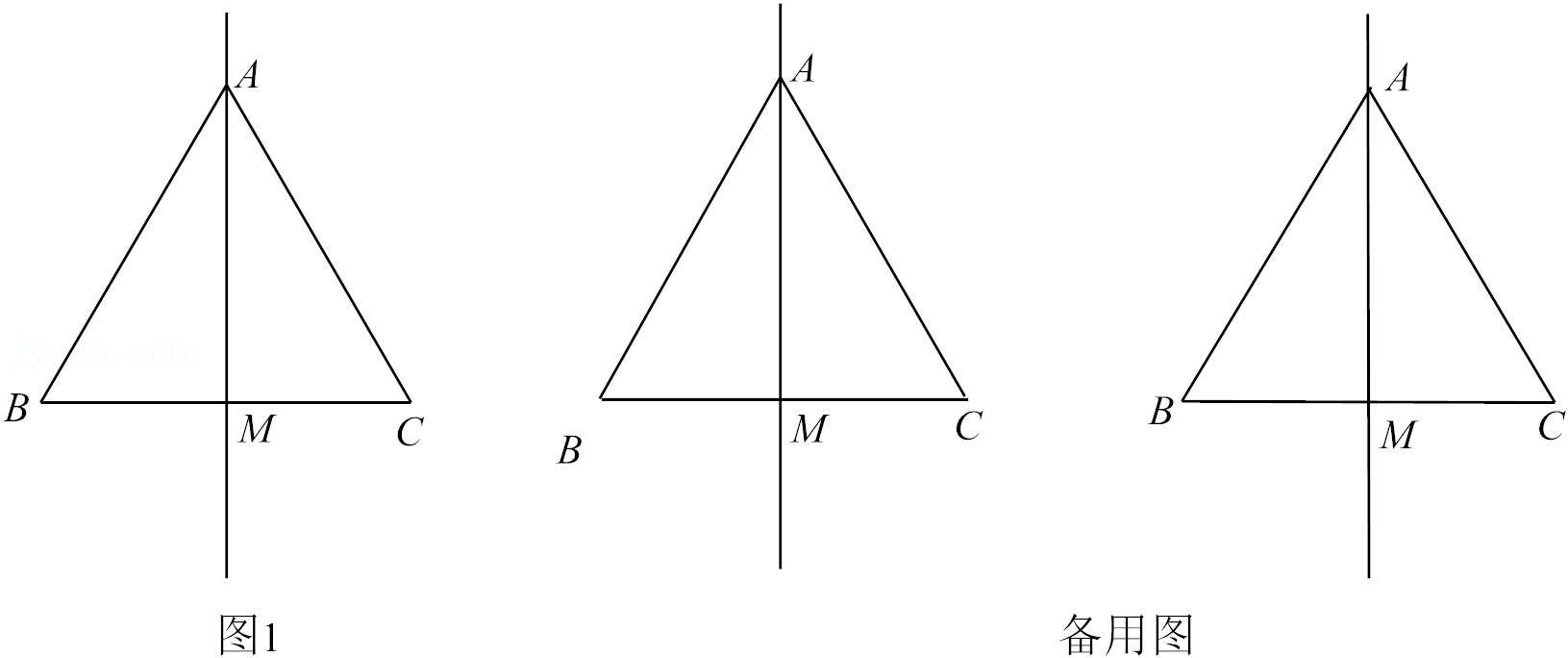
(1)当点D在线段AM上时，
①请在图1中补全图形；
②∠CAM的度数为 ；
③求证：△ADC≌△BEC；
(2)当点D在直线AM上时，直线BE与直线AM的交点为O(点D与点M不重合，点E与点O不重合)，直接写出线段OE，OM与OD的数量关系．
