试卷题目
1.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
- A.

- B.

- C.

- D.

2.一个多边形的内角和是外角和的2倍,这个多边形的边数是( )
- A. 4
- B. 6
- C. 8
- D. 10
3.如图,将△ABC一角折叠,若∠1+∠2=80°,则∠B+∠C=( )
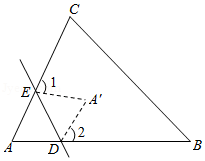

- A. 40°
- B. 100°
- C. 140°
- D. 160°
4.已知D是△ABC的边AB上一点,DF交AC于点E,DE=EF,FC//AB,若BD=2,CF=5,则AB的长为( )
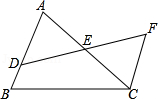

- A. 1
- B. 3
- C. 5
- D. 7
5.如图,△ABC中,∠CAB和∠CBA的角平分线交于点P,连接PA、PB、PC,若△PAB、△PBC、△PAC的面积分别为S1、S2、S3,则( )
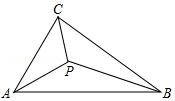

- A. S1<S2+S3
- B. S1=S2+S3
- C. S1>S2+S3
- D. 无法确定S1与(S2+S3)的大小
6.如图,在△ABC中,分别以点A和点C为圆心,大于
AC的长为半径作弧,两弧相交于点M、N,直线MN与AC、BC分别相交于E和D,连接AD,若AE=3cm,△ABC的周长为13cm,则△ABD的周长是( )
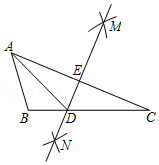
| 1 |
| 2 |

- A. 7cm
- B. 10cm
- C. 16cm
- D. 19cm
7.如图,∠MON=36°,点P是∠MON中的一定点,点A、B分别在射线OM、ON上移动.当△PAB的周长最小时,∠APB的大小为( )



















