试卷题目
1．围棋起源于中国，古代称之为“弈”，至今已有四千多年的历史．下列由黑、白棋子摆成的图案中，是轴对称图形的是( )
- A.
- B.
- C.
- D.
2．在△ABC中，AB=1，BC=4，则AC的长可能是( )
- A. 2
- B. 3
- C. 4
- D. 5
3．小明不小心将一块三角形玻璃打碎成了3块不规则的玻璃块(如图所示)，为了去玻璃店配一块与原玻璃形状、大小都一样的玻璃，小明应该带玻璃块( )
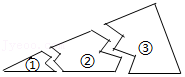
- A. ①
- B. ②
- C. ③
- D. 都可以
4．医用外科口罩的熔喷布厚度约为0.000136米，将0.000136用科学记数法表示应为( )
- A. 0.136×10-3
- B. 1.36×10-3
- C. 1.36×10-4
- D. 13.6×10-5
5．下列计算正确的是( )
- A. x2•x4=x8
- B. (2a3)3=6a9
- C. (1+x)(1-y)=1-xy
- D. 4m2n3÷mn=4mn2
6．如图，在正六边形ABCDEF中，连接BF，DF，则∠BFD的度数为( )
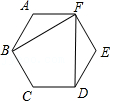
- A. 50°
- B. 60°
- C. 65°
- D. 70°
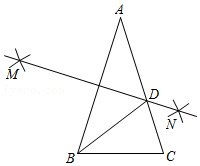
7．如图，在△ABC中，AB的垂直平分线DE与边AB，AC分别交于点D，E．已知△ABC与△BCE的周长分别为16cm和10cm，则BD的长为( )
- A. 3cm
- B. 4cm
- C. 5cm
- D. 6cm
8．若关于x的方程
-1=
无解，则m的值为( )
| 2x |
| x-3 |
| m-1 |
| 3-x |
- A. -5
- B. 7
- C. 5
- D. -3
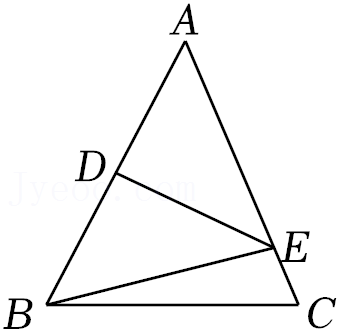
9．如图，在等边三角形ABC中，AD为BC边上的高，∠ABC与∠ACB的平分线交AD于点E．已知△CDE的面积为2，则△ABC的面积为( )
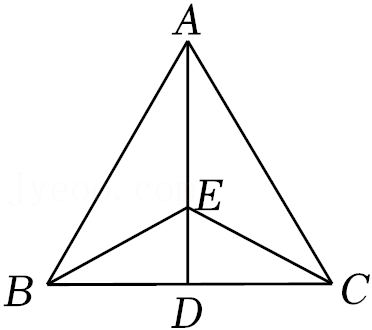
- A. 18
- B. 12
- C. 9
- D. 6
10．如图，在△ABC中，F是高AD、BE的交点，AD=BD，BC=6，CD=2，则线段AF的长度为( )
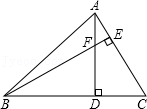
- A. 2
- B. 1
- C. 4
- D. 3
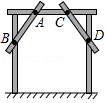
11．木工师傅在做好门框后，为了防止变形，常常按如图所示的方法钉上两根斜拉的木板条，其数学依据是三角形具有 ．
12．分解因式：a2-4ab+4b2= ．
13．若分式
的值为0，则m的值为 ．
| |m|-6 |
| m-6 |
14．若点A(a，3)与点B(-8，b)关于x轴对称，则ab= ．
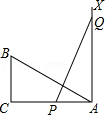
15．如图，∠C=90°，AC=10，BC=5，AX⊥AC，点P和点Q从A点出发，分别在线段AC和射线AX上运动，且AB=PQ，当点P运动到AP= ，△ABC与△APQ全等．
16．化简：a+1+a(a+1)+a(a+1)2+…+a(a+1)2022= ．
17．计算：(2a4b7-6ab2)÷2ab+(-ab2)3．
18．先化简，再求值：(
-
)÷
，其中x=3．
| 2x2+2x |
| x2-1 |
| x2-x |
| x2-2x+1 |
| x |
| x+1 |
19．如图，在平面直角坐标系中，已知点A(2，5)，B(2，1)，C(6，1)．
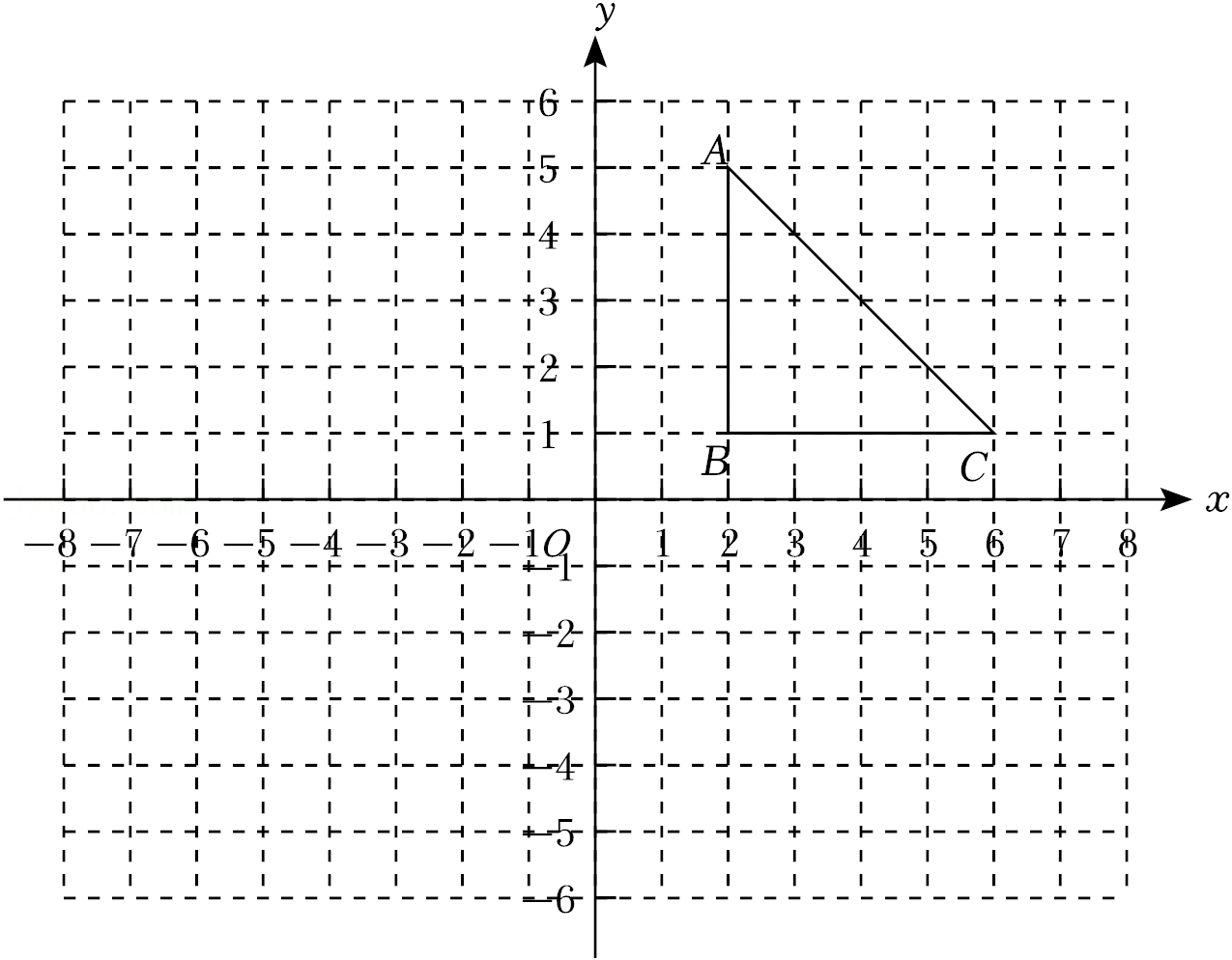
(1)画出△ABC关于y轴对称的△A1B1C1；
(2)在x轴上找一点P，使PB+PC的值最小(保留作图痕迹)，并写出点P的坐标．
(1)画出△ABC关于y轴对称的△A1B1C1；
(2)在x轴上找一点P，使PB+PC的值最小(保留作图痕迹)，并写出点P的坐标．
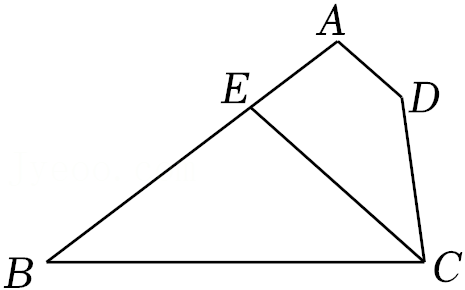
20．如图，在四边形ABCD中，∠A=100°，∠D=140°，∠BCD的平分线CE交AB于点E．
(1)若∠B=∠BCD，则∠B= °；
(2)若CE∥AD，求∠B的大小．
(1)若∠B=∠BCD，则∠B= °；
(2)若CE∥AD，求∠B的大小．
21．目前，步行已成为人们最喜爱的健身方法之一，通过手机可以计算行走的步数与相应的能量消耗，还可以通过运动做公益(如图)．对比手机数据发现小明步行12000步与小红步行9000步消耗的能量相同．若每消耗1千卡能量小明行走的步数比小红多10步，求小红，小明每消耗1千卡能量分别需要行走多少步？
22．已知a，b，c是△ABC的三边长．
(1)若a，b，c满足(a-b)(b-c)=0，试判断△ABC的形状；
(2)化简：|a+b-c|+|b-c-a|．
(1)若a，b，c满足(a-b)(b-c)=0，试判断△ABC的形状；
(2)化简：|a+b-c|+|b-c-a|．
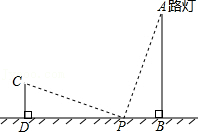
23．小明利用一根长3 m的竿子来测量路灯AB的高度．他的方法如下：如图，在路灯前选一点P，使BP=3m，并测得∠APB=70°，然后把竖直的竿子CD(CD=3m)在BP的延长线上左右移动，使∠CPD=20°，此时测得BD=11.2m．请根据这些数据，计算出路灯AB的高度．
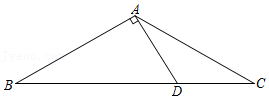
24．如图，等腰△ABC中，AB=AC，∠BAC=120°，AD⊥AB交BC于点D，AD=2，求BC的长．
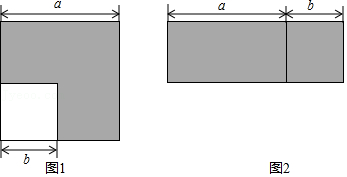
25．如图1，从边长为a的大正方形中剪去一个边长为b的小正方形，把剩下的阴影部分拼成如图2所示的长方形．
(1)上述操作能验证的公式是 ；
(2)请应用这个公式完成下列各题：
①已知4a2-b2=24，2a+b=6，则2a-b= ；
②计算：(1-
)(1-
)(1-
)…(1-
)．
(1)上述操作能验证的公式是 ；
(2)请应用这个公式完成下列各题：
①已知4a2-b2=24，2a+b=6，则2a-b= ；
②计算：(1-
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 20222 |
26．CD经过∠BCA顶点C的一条直线，CA=CB．E，F分别是直线CD上两点，且∠BEC=∠CFA=∠α．
(1)若直线CD经过∠BCA的内部，且E，F在射线CD上，请解决下面两个问题：
①如图1，若∠BCA=90°，∠α=90°，则BE CF；EF |BE-AF|(填“＞”，“＜”或“=”)；
②如图2，若0°＜∠BCA＜180°，请添加一个关于∠α与∠BCA关系的条件 ，使①中的两个结论仍然成立，并证明两个结论成立．
(2)如图3，若直线CD经过∠BCA的外部，∠α=∠BCA，请提出EF，BE，AF三条线段数量关系的合理猜想(不要求证明)．
(1)若直线CD经过∠BCA的内部，且E，F在射线CD上，请解决下面两个问题：
①如图1，若∠BCA=90°，∠α=90°，则BE CF；EF |BE-AF|(填“＞”，“＜”或“=”)；
②如图2，若0°＜∠BCA＜180°，请添加一个关于∠α与∠BCA关系的条件 ，使①中的两个结论仍然成立，并证明两个结论成立．
(2)如图3，若直线CD经过∠BCA的外部，∠α=∠BCA，请提出EF，BE，AF三条线段数量关系的合理猜想(不要求证明)．
