试卷题目
1.在二次根式
√x-2
中,x的取值范围是( )- A. x≥2
- B. x≥-2
- C. x>2
- D. x<2
2.下列各组中的三条线段,不能组成直角三角形的是( )
- A. 3,4,5
- B. 6,8,10
- C. 4,5,6
- D. 5,12,13
3.下列各式成立的是( )
- A. √6÷√2=√3
- B. √18=2√3
- C. √2×√3=√5
- D. √2+√3=√5
4.菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的面积是( )
- A. 48
- B. 24
- C. 20
- D. 16
5.下列四个命题,其逆命题成立的是( )
- A. 两直线平行,内错角相等
- B. 如果两个数相等,那么这两个数的绝对值相等
- C. 若a=b,则a2=b2
- D. 若√a=√b,则a=b
6.如图,一根木杆在离地面3m处折断,木杆顶端落在离木杆底端4m处,木杆折断之前的高度是( )


- A. 5m
- B. 6m
- C. 7m
- D. 8m
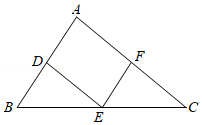
7.如图,在△ABC中,AB=4,AC=5,BC=6,点D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为( )

- A. 6
- B. 9
- C. 12
- D. 15
8.如图是某区域的平面示意图,码头A在观测站B的正东方向,码头A的北偏西60°方向上有一小岛C,小岛C在观测站B的北偏西15°方向上,码头A到小岛C的距离AC为(
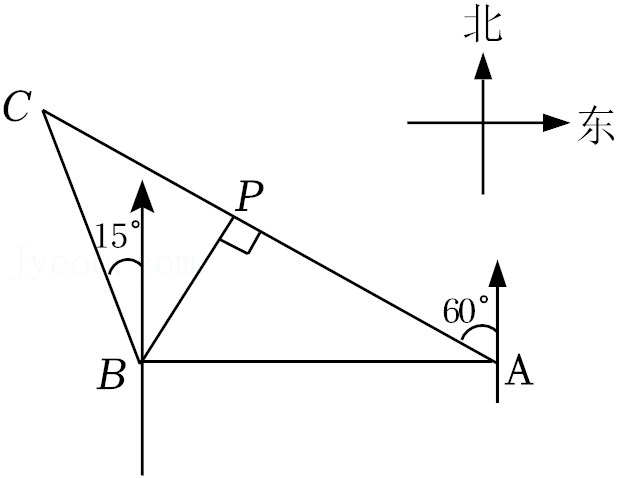
√3
+1)海里.观测站B到AC的距离BP是( )
- A. √3
- B. 1
- C. 2
- D. √3+1
2
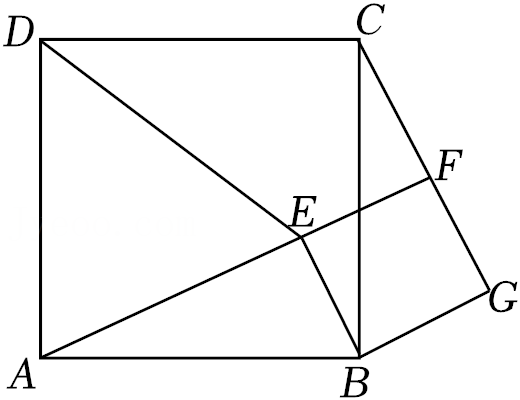
9.如图,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBG.延长AE交CG于点F,连接DE.下列结论:①AF⊥CG,②四边形BEFG是正方形,③若DA=DE,则CF=FG;其中正确的结论是( )

- A. ①②③
- B. ①②
- C. ②③
- D. ①③
10.如图,在正方形ABCD中,E、F是对角线AC上的两个动点,P是正方形四边上的任意一点,且AB=4,EF=2,设AE=x.当0<x<4

√2
-2,△PEF是等腰三角形时,下列关于P点个数的说法中,P点最多有( )
- A. 8个
- B. 10个
- C. 12个
- D. 14个
11.计算:
√25
的结果是 .12.如图,平行四边形ABCD中,AC,BD交于点O,且AC+BD=36,AB=11,则△AOB的周长是 .
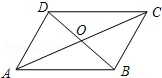

13.如图,在矩形ABCD中,AC,BD交于点O,△OAB是等边三角形,且AB=4.则矩形ABCD的面积是 .
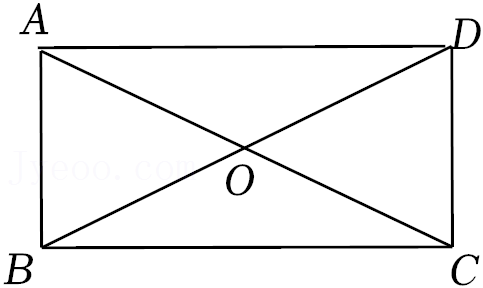

14.运用因式分解的方法可以求方程的解,如x2-5=(x+
√5
)(x-√5
),则方程x2-5=0的解为x=√5
或-√5
,用这种思想解高次方程x3-2x=0,它的解是 .15.如图,圆柱的高为6cm,底面周长为16cm,蚂蚁在圆柱侧面爬行,从点A爬到点B的最短路程是 cm.
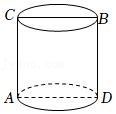

16.如图,在△ABC中AB=AC=10,BC=16,若∠BAD=3∠DAC,则CD= .
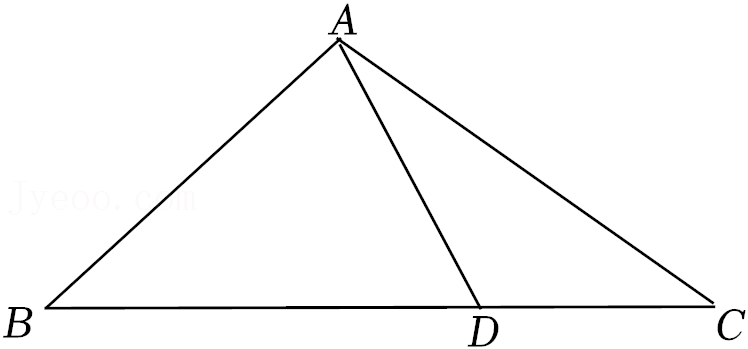

17.计算:
(1)4
(2)
(1)4
√3
×√3
÷√2
;(2)
√24
-2√6
+√18
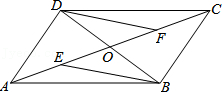
.18.如图,平行四边形ABCD的对角线AC、BD相交于点O,E、F分别是OA、OC的中点,求证:BE=DF.

19.实数x,y使
√x-3
+(y+2)2=0成立,求√xy
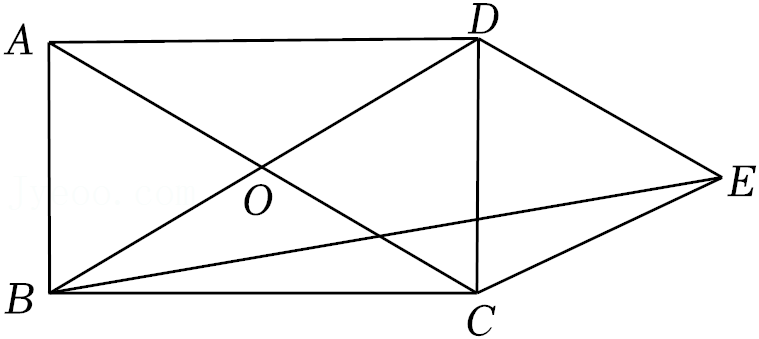
的值.20.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD,连接BE.
(1)求证:四边形OCED是菱形;
(2)若∠AOB=60°,AB=2,求BE的长.
(1)求证:四边形OCED是菱形;
(2)若∠AOB=60°,AB=2,求BE的长.

21.仅用无刻度直尺完成下列画图,保留作图痕迹,不需要写作法.
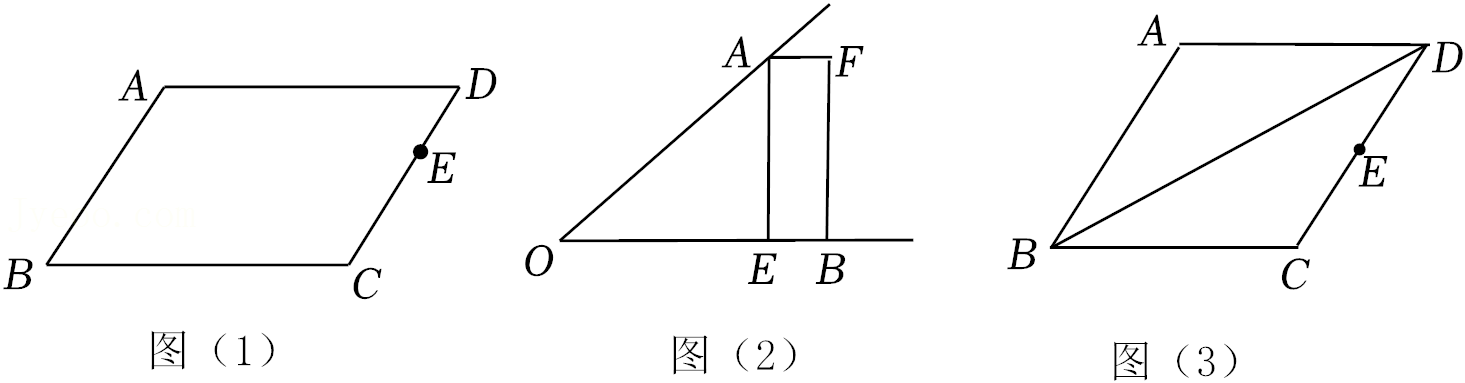
(1)如图(1),四边形ABCD为平行四边形,过点E作一条直线平分平行四边形ABCD的面积;
(2)如图(2),已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形,请你在图中画出∠AOB的平分线;
(3)如图(3),四边形ABCD为菱形,E为CD的中点,画出AD的中点P.
(1)如图(1),四边形ABCD为平行四边形,过点E作一条直线平分平行四边形ABCD的面积;
(2)如图(2),已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形,请你在图中画出∠AOB的平分线;
(3)如图(3),四边形ABCD为菱形,E为CD的中点,画出AD的中点P.

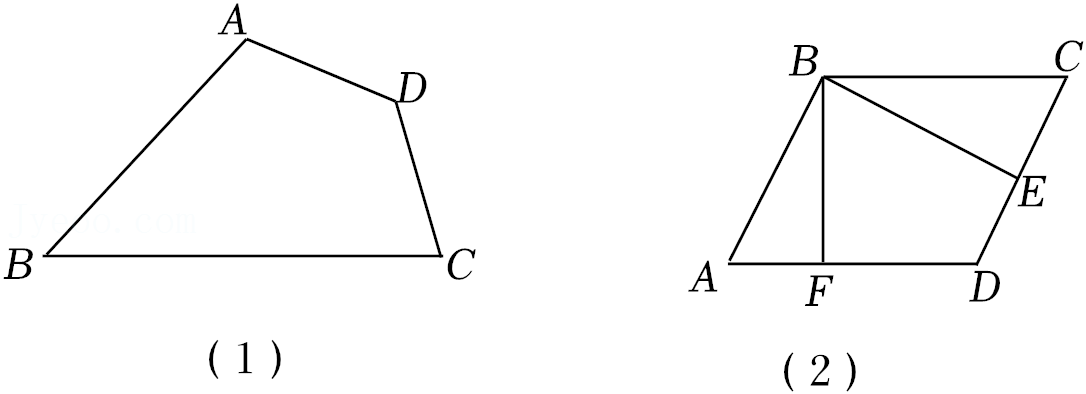
22.定义:有一组邻边相等且对角互补的四边形叫作“等补四边形”.例如,如图(1)四边形ABCD中,AD=DC,∠A+∠C=180°,则四边形ABCD是“等补四边形”.
(1)在以下四种图形中:①平行四边形,②菱形,③矩形,④正方形,一定是“等补四边形”的是 .
(2)如图(2),在菱形ABCD中,∠A=60°,E,F分别是CD,AD边上的动点(不与点A,D,C重合),且AF=DE.求证:四边形BEDF为等补四边形.
(1)在以下四种图形中:①平行四边形,②菱形,③矩形,④正方形,一定是“等补四边形”的是 .
(2)如图(2),在菱形ABCD中,∠A=60°,E,F分别是CD,AD边上的动点(不与点A,D,C重合),且AF=DE.求证:四边形BEDF为等补四边形.

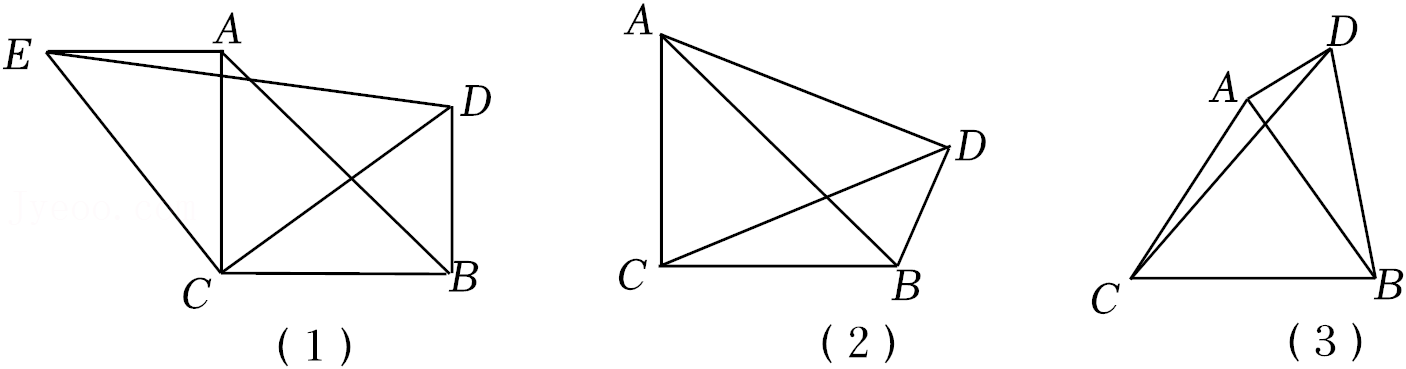
23.(1)问题背景 如图(1),已知△ABC和△DCE为等腰直角三角形,CA=CB,CE=CD,求证:△CBD≌△CAE.
(2)尝试应用 如图(2),已知△ACB,CA=CB,∠ACB=90°,点D是△ABC外一点,且∠ADC=45°,求证:AD2+BD2=2AC2.
(3)拓展创新 如图(3),点D是等边三角形ABC外一点,若DC=10,DB=6
(2)尝试应用 如图(2),已知△ACB,CA=CB,∠ACB=90°,点D是△ABC外一点,且∠ADC=45°,求证:AD2+BD2=2AC2.
(3)拓展创新 如图(3),点D是等边三角形ABC外一点,若DC=10,DB=6
√2
,DA=2,直接写出∠ADB的大小.
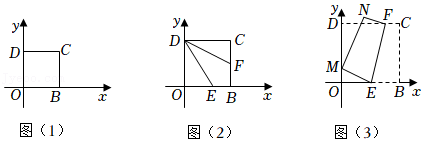
24.如图(1),四边形OBCD正方形,O,D两点的坐标分别是(0,0),(0,4).
(1)直接写出点C的坐标是 ;
(2)如图(2),点F为线段BC的中点,点E在线段OB上,若∠EDF=∠CDF,求点E的坐标;
(3)如图(3),动点E,F分别在边OB,CD上,将正方形OBCD沿直线EF折叠,使点B的对应点M始终落在边OD上(点M不与点O,D重合),点C落在点N处,设OM=x,四边形BEFC的面积为S,请求出S与x的关系式.
(1)直接写出点C的坐标是 ;
(2)如图(2),点F为线段BC的中点,点E在线段OB上,若∠EDF=∠CDF,求点E的坐标;
(3)如图(3),动点E,F分别在边OB,CD上,将正方形OBCD沿直线EF折叠,使点B的对应点M始终落在边OD上(点M不与点O,D重合),点C落在点N处,设OM=x,四边形BEFC的面积为S,请求出S与x的关系式.