试卷题目
1.下列长度的三条线段能组成三角形的是( )
- A. 3,4,8
- B. 5,6,11
- C. 5,6,10
- D. 4,5,9
2.下列计算正确的是( )
- A. b2•b2=2b2
- B. x4•x4=x16
- C. (-2a)2=4a2
- D. (m2)3•m4=m9
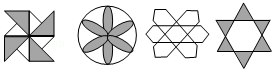
3.下列图形中,轴对称图形的个数是( )

- A. 1
- B. 2
- C. 3
- D. 4
4.若分式
的值为零,则a的值是( )
| a2-4 |
| a+2 |
- A. ±2
- B. 2
- C. -2
- D. 0
5.已知2m=3,32n=6,则下列关系成立的是( )
- A. m+1=5n
- B. n=2m
- C. m+1=n
- D. 2m=5+n
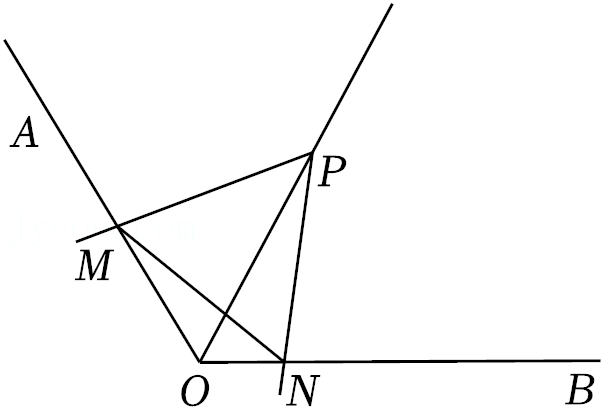
6.如图,P是∠AOB平分线上一点,OP=10,∠AOB=120°,在绕点P旋转的过程中始终保持∠MPN=60°不变,其两边和OA,OB分别相交于M,N,下列结论:①△PMN是等边三角形;②MN的值不变;③OM+ON=10;④四边形PMON面积不变.其中正确结论的个数为( )

- A. 4
- B. 3
- C. 2
- D. 1
7.若点A(2,-1)与点A'(m,n)关于x轴对称,则m+n= .
8.已知多边形的每个内角都等于120°,则这个多边形是 边形.
9.计算
+
的结果是 .
| a |
| a-1 |
| 1 |
| 1-a |
10.已知a+b=5,ab=3,则a2+b2= .
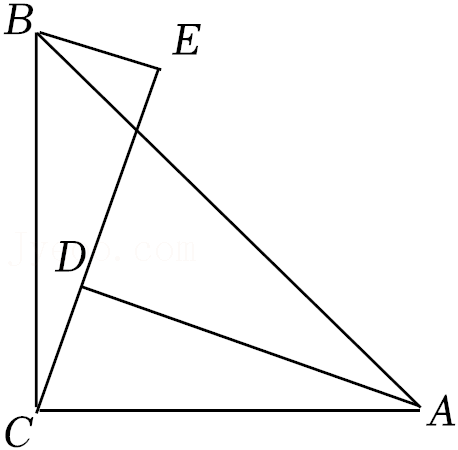
11.如图,在△ABC中,AB=AC,AD,CE是△ABC的两条中线,AD=5,CE=6,P是AD上一个动点,BP+EP的最小值是 .


12.规定:在直角三角形中,如果直角边是斜边的一半,那么它所对的锐角为30°.等腰三角形ABC中,AD⊥BC于点D,若AD=
BC,则△ABC底角的度数为 .
| 1 |
| 2 |
13.计算:(2x+3)(2x-3)-4x(x-1).
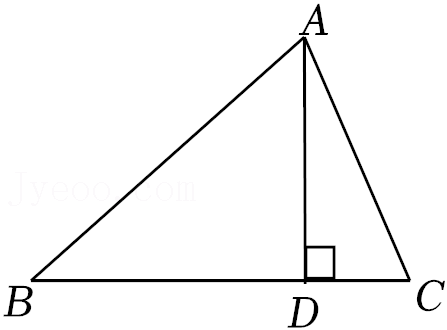
14.如图,AD⊥BC,∠BAD=48°,∠C=65°,求∠BAC的度数.

15.先化简,再求值:
÷(1-
),其中x与2,3构成等腰三角形.
| x2-2x+1 |
| x2-1 |
| 3 |
| x+1 |
16.如图,∠ACB=90°,∠BAC=45°,AD⊥CE,BE⊥CE,垂足分别是D,E,BE=0.8,DE=1.7,求AD的长.

17.如图,AD与BC相交于点O,AB=CD,∠ABC=∠CDA,EB=ED,求证:OE⊥BD.


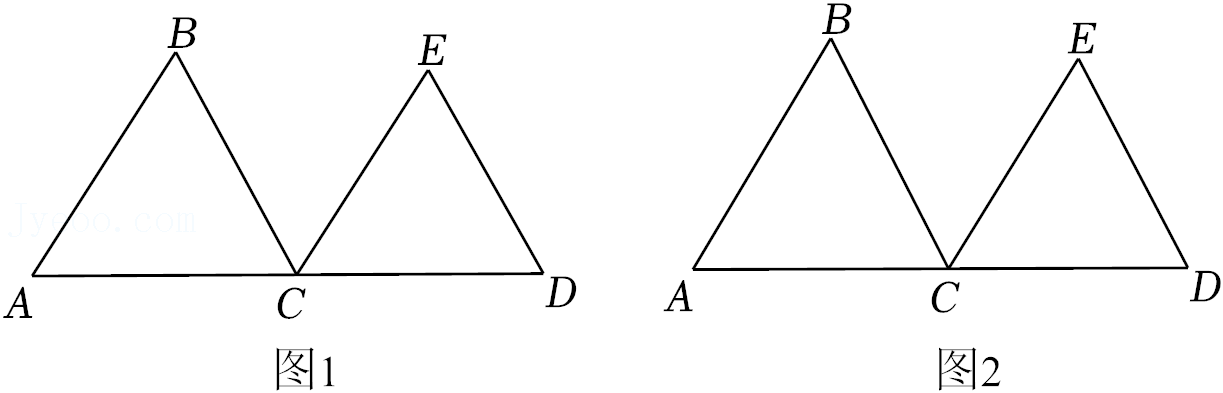
18.如图,△ABC和△DCE是全等的等边三角形,点A,C,D在一条直线上,请仅用无刻度直尺,完成以下作图(保留作图痕迹).
(1)在图1中,以AD为边作一个直角三角形;
(2)在图2中,作出AD的平行线段PQ=
AD.
(1)在图1中,以AD为边作一个直角三角形;
(2)在图2中,作出AD的平行线段PQ=
| 1 |
| 4 |

19.某校为进一步开展体育中考训练,购买了一批篮球和排球,已知购买的排球数量是篮球的2倍,购买排球用去了4000元,购买篮球用去了2520元,篮球单价比排球贵26元,求篮球、排球的单价.
20.观察下列各式:
(a-b)(a+b)=a2-b2;
(a-b)(a2+ab+b2)=a3-b3;
(a-b)(a3+a2b+ab2+b3)=a4-b4;
…
根据这一规律计算:
(1)(a-b)(a4+a3b+a2b2+ab3+b4)= ;
(a-b)(an+an-1b+an-2b2+…+abn-1+bn)= ;
(2)22021+22020+22019+…+22+2+1.
(a-b)(a+b)=a2-b2;
(a-b)(a2+ab+b2)=a3-b3;
(a-b)(a3+a2b+ab2+b3)=a4-b4;
…
根据这一规律计算:
(1)(a-b)(a4+a3b+a2b2+ab3+b4)= ;
(a-b)(an+an-1b+an-2b2+…+abn-1+bn)= ;
(2)22021+22020+22019+…+22+2+1.
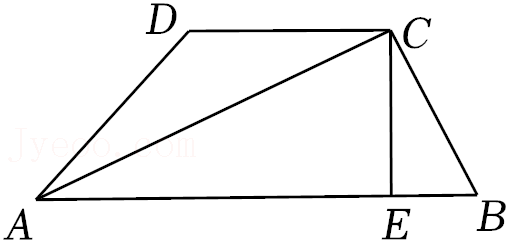
21.如图,在四边形ABCD中,∠DAB和∠DCB互补,CD=CB,CE⊥AB于E.
(1)求证:AC平分∠DAB;
(2)试猜想AB,AD,AE的数量关系并证明你的猜想.
(1)求证:AC平分∠DAB;
(2)试猜想AB,AD,AE的数量关系并证明你的猜想.

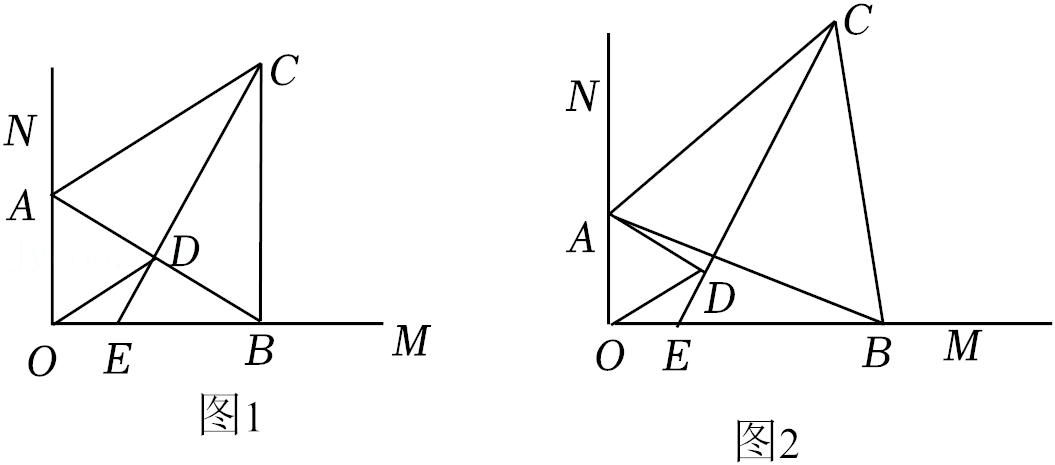
22.已知∠MON=90°,点A在边ON上,且OA=4,点B在边OM上运动,分别以OA、AB为边在∠MON内部作等边三角形AOD,等边三角形ABC,连接CD并延长交OM于点E.
(1)如图1所示,当点A,D,B共线时,∠ABO和∠ACD的关系是 ,OE和DE的关系是 ;
(2)如图2所示,当点B运动到任何位置时,(1)中的结论是否仍然成立,如果成立,请给出证明,若不成立,请给出你所探究到的结论并给出证明;
(3)在点B的运动过程中四边形AOED的面积 (填“变化”或者“不变”),当运动到OB=4时,△ADC的面积为 .
(1)如图1所示,当点A,D,B共线时,∠ABO和∠ACD的关系是 ,OE和DE的关系是 ;
(2)如图2所示,当点B运动到任何位置时,(1)中的结论是否仍然成立,如果成立,请给出证明,若不成立,请给出你所探究到的结论并给出证明;
(3)在点B的运动过程中四边形AOED的面积 (填“变化”或者“不变”),当运动到OB=4时,△ADC的面积为 .






