试卷题目
1．若分式
有意义，则x的取值范围是( )
| 1 |
| x-2 |
- A. x≠2
- B. x=2
- C. x＞2
- D. x＜2
2．在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是( )
- A.
- B.
- C.
- D.
3．以下列长度的各组线段为边，能组成三角形的是( )
- A. 2cm，4cm，6cm
- B. 2cm，5cm，9cm
- C. 7cm，8cm，10cm
- D. 6cm，6cm，13cm
4．计算
+
的结果是( )
| x |
| x+1 |
| 1 |
| x+1 |
- A.
x x+1 - B.
1 x+1 - C. 1
- D. -1
5．计算(-2x+1)(-3x2)的结果为( )
- A. 6x3+1
- B. 6x3-3
- C. 6x3-3x2
- D. 6x3+3x2
6．如图，△ABN≌△ACM，∠B和∠C是对应角，AB和AC是对应边，则下列结论中一定成立的是( )
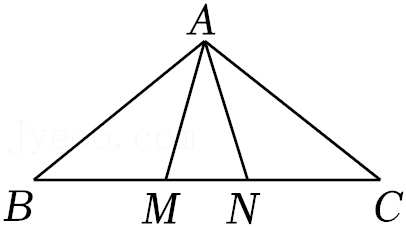
- A. ∠BAM=∠MAN
- B. AM=CN
- C. ∠BAM=∠ABM
- D. AM=AN
7．下列运算正确的是( )
- A. (5-m)(5+m)=m2-25
- B. (1-3m)(1+3m)=1-3m2
- C. (-4-3n)(-4+3n)=-9n2+16
- D. (2ab-n)(2ab+n)=4ab2-n2
8．下列计算正确的是( )
- A. (2a+b)2=4a2+b2
- B. (5x-2y)2=25x2-10xy+4y2
- C. (x-y)2=
1 2 x2-xy+y21 2 - D. (x+
1 2 )2=1 3 x2+1 4 x+1 3 1 9
9．把多项式x2+3x-54分解因式，其结果是( )
- A. (x+6)(x-9)
- B. (x-6)(x+9)
- C. (x+6)(x+9)
- D. (x-6)(x-9)
10．分式方程
-
=
的解是( )
| 3 |
| 2 |
| 1 |
| 3x-1 |
| 7 |
| 6x-2 |
- A. x=
2 9 - B. x=
3 4 - C. x=1
- D. x=
4 3
11．如图，在△ABC中，AB=AC，AD、CE是△ABC的两条中线，P是AD上一个动点，则下列线段的长度等于BP+EP最小值的是( )
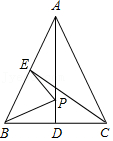
- A. BC
- B. CE
- C. AD
- D. AC
12．如图所示，AD平分∠BAC，AB=AC，连接BD、CD并延长分别交AC、AB于F、E点，则此图中全等三角形的对数为( )
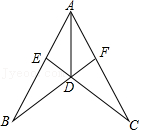
- A. 2对
- B. 3对
- C. 4对
- D. 5对
13．计算(
√3
+1)(√3
-1)的结果等于 ．14．若x=2是关于x的分式方程
+
=2的解，则a的值等于 ．
| 2 |
| x |
| a |
| x-1 |
15．一个多边形的内角和是它外角和的2倍，则它的边数是 ．
16．如图，在Rt△ABC中，∠C=90°，AD=ED，∠CDE=72°，则∠B的大小等于 (度)．
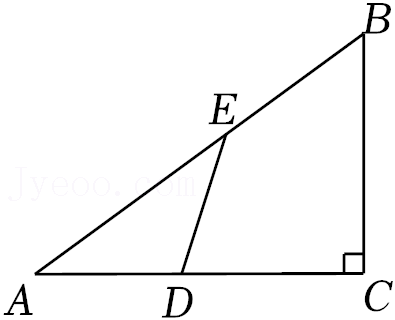
17．当x=
时，计算
÷
的结果等于 ．
| 1 |
| 2 |
| x2-4x+4 |
| x2-4 |
| x-2 |
| x2+2x |
18．如图，在Rt△ABC中，∠A=90°，AB=4，AC=2．
(1)△ABC的面积等于 ；
(2)P为线段AB上一点，过点P作PQ⊥BC，垂足为Q．当PQ=PA时，请在如图所示的矩形区域内，用无刻度的直尺和圆规，画出线段PQ，并简要说明点P和点Q的位置是如何找到的(保留作图痕迹，不要求证明)．
(1)△ABC的面积等于 ；
(2)P为线段AB上一点，过点P作PQ⊥BC，垂足为Q．当PQ=PA时，请在如图所示的矩形区域内，用无刻度的直尺和圆规，画出线段PQ，并简要说明点P和点Q的位置是如何找到的(保留作图痕迹，不要求证明)．
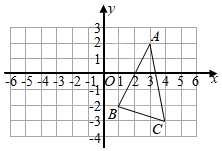
19．在平面直角坐标系中，△ABC的顶点A，B，C的坐标分别为(3，2)，(1，-2)，(4，-3)．△A′B′C′与△ABC关于y轴对称，点A，B，C的对应点分别为A′，B′，C′．请在图中作出△A′B′C′，并写出点A′，B′，C′的坐标．
20．如图，在△ABC中，CD是∠ACB的平分线，点E在边AC上，且DE=CE．
(1)求证：DE∥BC；
(2)若∠A=50°，∠B=60°，求∠BDC的大小．
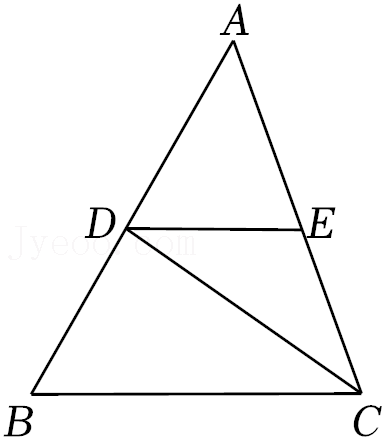
(1)求证：DE∥BC；
(2)若∠A=50°，∠B=60°，求∠BDC的大小．
21．(1)先化简，再求值：[(2a+b)2+(b+2a)(b-2a)-2b(a+2b)]÷2b，其中a=
，b=
；
(2)分解因式：
①x3-9x；
②6xy2-9x2y-y3．
| 1 |
| 2 |
| 1 |
| 3 |
(2)分解因式：
①x3-9x；
②6xy2-9x2y-y3．
22．在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E，F．
(1)若BE=CF，求证：AD是△ABC的角平分线．
(2)若AD是△ABC的角平分线，求证：BE=CF．
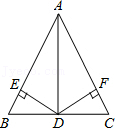
(1)若BE=CF，求证：AD是△ABC的角平分线．
(2)若AD是△ABC的角平分线，求证：BE=CF．
23．一辆汽车开往距离出发地180千米的目的地，出发后第一小时内按原计划的速度匀速行驶，一小时后以原来速度的1.5倍匀速行驶，并比原计划提前40分到达目的地．求前一小时的行驶速度．
24．如图，在△AOB和△COD中，OA=OB，OC=OD，OA＜OC，∠AOB=∠COD=36°．连接AC，BD交于点M，连接OM．
(1)求证：AC=BD；
(2)求∠AMB的大小；
(3)求证：∠AMO=∠DMO．
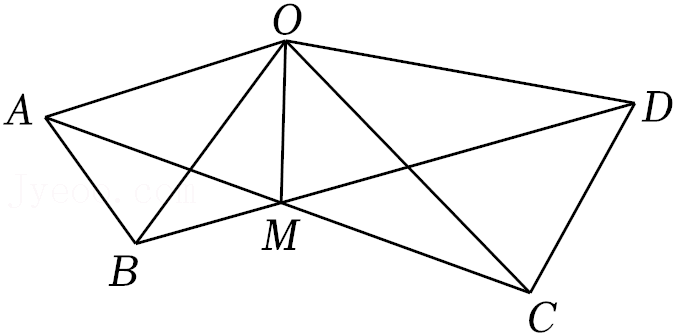
(1)求证：AC=BD；
(2)求∠AMB的大小；
(3)求证：∠AMO=∠DMO．
