试卷题目
1.下列长度的三条线段能组成三角形的是( )
- A. 1,2,3
- B. 1,3,5
- C. 3,4,7
- D. 4,5,6
2.一定能确定△ABC≌△DEF的条件是( )
- A. ∠A=∠D,AB=DE,∠B=∠E
- B. ∠A=∠E,AB=EF,∠B=∠D
- C. AB=DE,BC=EF,∠A=∠D
- D. ∠A=∠D,∠B=∠E,∠C=∠F
3.在下列各图的△ABC中,正确画出AC边上的高的图形是( )
- A.

- B.

- C.

- D.

4.第24届冬季奥林匹克运动会,将于2025年02月04日~2025年02月20日在中华人民共和国北京市和张家口市联合举行.在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案上的一部分图形,其中不是轴对称图形的是( )
- A.

- B.

- C.

- D.

5.若等腰三角形的一条边长等于4,另一条边长为9,则这个三角形的周长是( )
- A. 17
- B. 22
- C. 17或22
- D. 13
6.如图,△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A'处,折痕为CD,则∠A'DB=( )
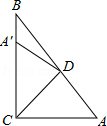

- A. 40°
- B. 30°
- C. 20°
- D. 10°
7.如图,已知△ABC中,AC+BC=24,AO,BO分别是角平分线,且MN//BA,分别交AC于N,BC于M,则△CMN的周长为( )
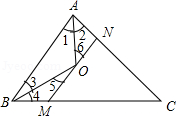

- A. 12
- B. 24
- C. 36
- D. 不确定
8.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.
如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
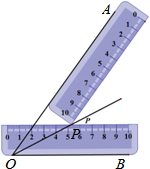
如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

- A. 角的内部到角的两边的距离相等的点在角的平分线上
- B. 角平分线上的点到这个角两边的距离相等
- C. 三角形三条角平分线的交点到三条边的距离相等
- D. 以上均不正确
9.如图,在△ABC中,AB=AC,∠C=70°,△AB'C'与△ABC关于直线EF对称,∠CAF=10°,连接BB',则∠ABB'的度数是( )
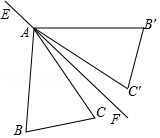

- A. 30°
- B. 35°
- C. 40°
- D. 45°
10.如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①AP⊥BC;②AS=AR;③QP//AR;④△BRP≌△QSP.正确的有( )
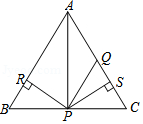

- A. 1个
- B. 2个
- C. 3个
- D. 4个
11.点(-3,-5)关于y轴对称的点的坐标是 .
12.如图,已知线段AB、CD相交于点O,且∠A=∠B,只需补充一个条件 ,则有△AOC≌△BOD.

13.用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC= 度.


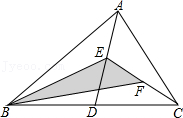
14.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积等于4cm2,则阴影部分图形面积等于 cm2.

15.等腰三角形一腰上的高与另一边的夹角为40°,则这个等腰三角形顶角的度数为 .
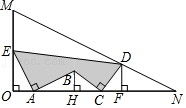
16.如图,点A,C,D,E在△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD且BC=CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为 .

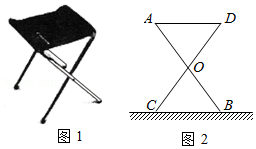
17.某中学计划为新生配备如图1所示的折叠凳,图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为35cm,由以上信息能求出CB的长度吗?如果能,请求出CB的长度;如果不能,请说明理由.

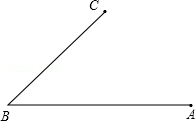
18.作图题:在∠ABC内找一点P,使它到∠ABC的两边的距离相等,
并且到点A、C的距离也相等.(写出作法,保留作图痕迹)
并且到点A、C的距离也相等.(写出作法,保留作图痕迹)

19.如图,△ABC中,AB=AC=CD,BD=AD,求△ABC中各角的度数.

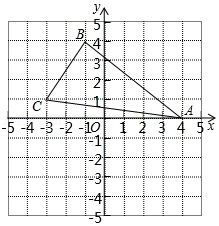
20.如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(-1,4),C(-3,1)
(1)在图中作△A'B'C',使△A'B'C'和△ABC关于x轴对称;
(2)写出点A',B',C'的坐标;
(3)求△ABC的面积.
(1)在图中作△A'B'C',使△A'B'C'和△ABC关于x轴对称;
(2)写出点A',B',C'的坐标;
(3)求△ABC的面积.

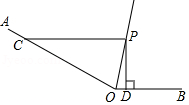
21.如图,∠AOB=150°,OP平分∠AOB,PD⊥OB于点D,PC//OB交OA于点C,若PD=3,求OC的长.

22.对于平面直角坐标系中任一点(a,b),规定三种变换如下:
①A(a,b)=(-a,b).如:A(7,3)=(-7,3);
②B(a,b)=(b,a).如:B(7,3)=(3,7);
③C(a,b)=(-a,-b).如:C(7,3)=(-7,-3);例如:A(B(2,-3))=A(-3,2)=(3,2)
规定坐标的部分规则与运算如下:
①若a=b,且c=d,则(a,c)=(b,d);反之若(a,c)=(b,d),则a=b,且c=d.
②(a,c)+(b,d)=(a+b,c+d);
(a,c)-(b,d)=(a-b,c-d).
例如:A(B(2,-3))+C(B(2,-3))=A(-3,2)+C(-3,2)=(3,2)+(3,-2)=(6,0).
请回答下列问题:
(1)化简:A(C(5,-3))= (填写坐标);
(2)化简:C(A(-3,-2))-B(C(-1,-2))= (填写坐标);
(3)若A(B(2x,-kx))-C(A(1+y,-2))=C(B(ky-1,-1))+A(C(y,x)),且k为整数,点P(x,y)在第四象限,求满足条件的k的所有可能取值.
①A(a,b)=(-a,b).如:A(7,3)=(-7,3);
②B(a,b)=(b,a).如:B(7,3)=(3,7);
③C(a,b)=(-a,-b).如:C(7,3)=(-7,-3);例如:A(B(2,-3))=A(-3,2)=(3,2)
规定坐标的部分规则与运算如下:
①若a=b,且c=d,则(a,c)=(b,d);反之若(a,c)=(b,d),则a=b,且c=d.
②(a,c)+(b,d)=(a+b,c+d);
(a,c)-(b,d)=(a-b,c-d).
例如:A(B(2,-3))+C(B(2,-3))=A(-3,2)+C(-3,2)=(3,2)+(3,-2)=(6,0).
请回答下列问题:
(1)化简:A(C(5,-3))= (填写坐标);
(2)化简:C(A(-3,-2))-B(C(-1,-2))= (填写坐标);
(3)若A(B(2x,-kx))-C(A(1+y,-2))=C(B(ky-1,-1))+A(C(y,x)),且k为整数,点P(x,y)在第四象限,求满足条件的k的所有可能取值.
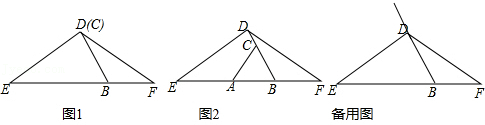
23.在△DEF中,DE=DF,点B在EF边上,且∠EBD=60°,C是射线BD上的一个动点(不与点B重合,且BC≠BE),在射线BE上截取BA=BC,连接AC.
(1)当点C在线段BD上时,
①若点C与点D重合,请根据题意补全图1,并直接写出线段AE与BF的数量关系为 ;
②如图2,若点C不与点D重合,请证明AE=BF+CD;
(2)当点C在线段BD的延长线上时,用等式表示线段AE,BF,CD之间的数量关系(直接写出结果,不需要证明).
(1)当点C在线段BD上时,
①若点C与点D重合,请根据题意补全图1,并直接写出线段AE与BF的数量关系为 ;
②如图2,若点C不与点D重合,请证明AE=BF+CD;
(2)当点C在线段BD的延长线上时,用等式表示线段AE,BF,CD之间的数量关系(直接写出结果,不需要证明).

24.在△ABC中,
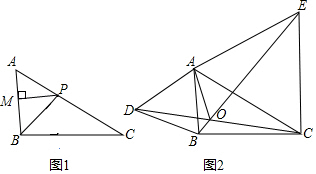
(1)如图1,BP为△ABC的角平分线,PM⊥AB于M,PN⊥BC于N,AB=50,BC=60请补全图形,并直接写出△ABP与△BPC面积的比值;
(2)如图2,分别以△ABC的边AB、AC为边向外作等边三角形ABD和ACE,CD与BE 相交于点O,求证:BE=CD;
(3)在(2)的条件下判断∠AOD与∠AOE的数量关系.(不需证明)

(1)如图1,BP为△ABC的角平分线,PM⊥AB于M,PN⊥BC于N,AB=50,BC=60请补全图形,并直接写出△ABP与△BPC面积的比值;
(2)如图2,分别以△ABC的边AB、AC为边向外作等边三角形ABD和ACE,CD与BE 相交于点O,求证:BE=CD;
(3)在(2)的条件下判断∠AOD与∠AOE的数量关系.(不需证明)





