试卷题目
1.64的立方根是( )
- A. -4
- B. 4
- C. ±4
- D. 不存在
2.下列运算正确的是( )
- A. (x3)3=x6
- B. (a+5)0=1
- C. √9=3
- D. x8÷x4=x2
3.四个实数5,0,
√8
,√3
,中,最大的无理数是( )- A. √3
- B. 0
- C. √8
- D. 5
4.若分式
的值为0,则x的值为( )
| x2-9 |
| x+3 |
- A. 4
- B. -4
- C. 3或-3
- D. 3
5.一个正方形的面积是18,估计它的边长的大小在( )
- A. 2与3之间
- B. 3与4之间
- C. 4与5之间
- D. 5与6之间
6.若m>n,则下列不等式正确的是( )
- A. m-6<n-6
- B. >
m 6 n 6 - C. 6m<6n
- D. -6m>-6n
7.在y=
中,自变量x的取值范围是( )
√x+2 |
| x-1 |
- A. x≥-1
- B. -1≤x≤2
- C. x≥-2
- D. x≥-2且x≠1
8.如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
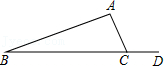

- A. 120°
- B. 90°
- C. 100°
- D. 30°
9.如图,在△ABC中,∠B=32°,∠BAC的平分线AD交BC于点D,若DE垂直平分AB,则∠C的度数为( )
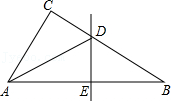

- A. 90°
- B. 84°
- C. 64°
- D. 58°
10.已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.
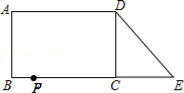

- A. 1
- B. 1或3
- C. 1或7
- D. 3或7
11.0.0000536用科学记数法可表示为 .
12.x的3倍减去2的差不小于0,列出不等式为 .
13.化简:
√8
-√2
= .14.计算:
-
= .
| x2 |
| x-1 |
| x |
| x-1 |
15.如图,点D、E分别在线段AB,AC上,AE=AD,不添加新的线段和字母,要使△ABE≌△ACD,需添加的一个条件是 (只写一个条件即可).
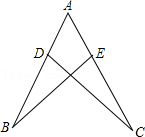

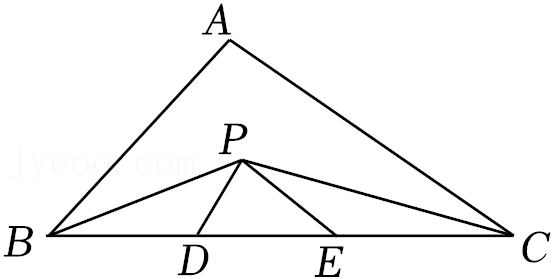
16.如图,在△ABC中,BC=15厘米,BP,CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则△PDE的周长为 .

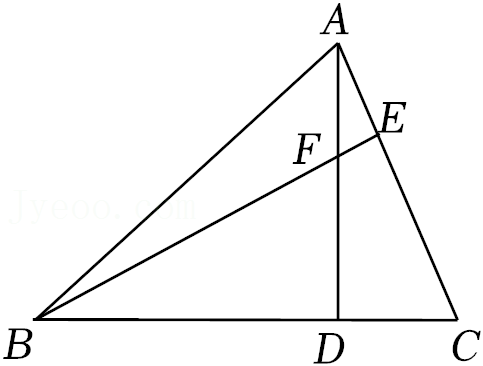
17.如图,在△ABC中,∠ABC=45°,F是高AD和BE的交点,AC=8cm,则线段BF的长度为 .

18.若x<2,化简
√(x-2)2
-|3-x|= .19.计算:(-2)2-20+(
)-1+
| 1 |
| 2 |
3√-8
-√9
20.已知A=
+
(1)化简A;
(2)若a是面积为8的某正方形的边长,求A的值.
| a2-9 |
| a(a+3)2 |
| 6 |
| a(a+3) |
(1)化简A;
(2)若a是面积为8的某正方形的边长,求A的值.
21.如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
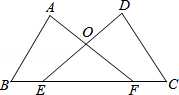
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.

22.阅读下列材料,然后回答问题
在进行二次根式去分母时,我们有时会碰上如
,
这样的式子,其实我们还可以将其进一步化简:
=
=
;①
;②
=
=
=
以上这种化简的步骤叫做分母有理化.
还可以用以下方法化简:
=
=
=
=
(1)请用不同的方法化简
.
参照③式得
= ;
参照④式得
= .
(2)化简:
+
+
+⋯+
(n=1,2,3,⋯).
在进行二次根式去分母时,我们有时会碰上如
| 5 |
√3 |
√
,| 2 |
| 3 |
| 2 |
√3 +1 |
| 5 |
√3 |
| 5× √3 |
√3 ×√3 |
| 5 √3 |
| 3 |
√
=| 2 |
| 3 |
√
=| 2×3 |
| 3×3 |
√6 |
| 3 |
| 2 |
√3 +1 |
| 2×( √3 -1) |
| ( √3 +1)(√3 -1) |
| 2( √3 -1) |
| ( √3 )2-12 |
√3
-1.③以上这种化简的步骤叫做分母有理化.
| 2 |
√3 +1 |
| 2 |
√3 +1 |
| 3-1 |
√3 +1 |
| ( √3 )2-12 |
√3 +1 |
| ( √3 +1)(√3 -1) |
√3 +1 |
√3
-1.④(1)请用不同的方法化简
| 2 |
√5 +√3 |
参照③式得
| 2 |
√5 +√3 |
参照④式得
| 2 |
√5 +√3 |
(2)化简:
| 1 |
√3 +1 |
| 1 |
√5 +√3 |
| 1 |
√7 +√5 |
| 1 |
√2n+1 +√2n-1 |
23.解不等式组
把它的解集表示在数轴上,并求出这个不等式组的整数解.
| { |
|
24.(1)在实数范围内定义运算“⊕”,其法则为:a⊕b=a2-b2,求方程(4⊕3)⊕x=24的解.
(2)已知2a的平方根是±2,3是3a+b的立方根,求a-2b的值.
(2)已知2a的平方根是±2,3是3a+b的立方根,求a-2b的值.
25.某商场在端午节来临之际用3000元购进A、B两种玩具110个,购买A玩具与购买B玩具的费用相同.已知A玩具的单价是B玩具单价的1.2倍.
(1)求A、B两种玩具的单价各是多少?
(2)若计划用不超过7000元的资金再次购进A、B两种玩具共260个,已知A、B两种玩具的进价不变.求A种玩具最多能购进多少个?
(1)求A、B两种玩具的单价各是多少?
(2)若计划用不超过7000元的资金再次购进A、B两种玩具共260个,已知A、B两种玩具的进价不变.求A种玩具最多能购进多少个?
26.如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.
①求证:△AEF≌△BCF;
②求证:AE=2BD.
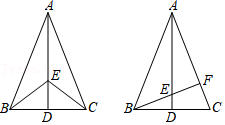
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.
①求证:△AEF≌△BCF;
②求证:AE=2BD.






