试卷题目
1.
√x-1
中x的取值范围是( )- A. x≥0
- B. x≥-1
- C. x≥1
- D. x>1
2.下列图形中,是轴对称图形的是( )
- A.

- B.

- C.

- D.

3.下列分式是最简分式的是( )
- A.
2x x2+2 - B.
x+1 x2-1 - C.
4 2x - D.
2-x x-2
4.下列由左边到右边的变形,( )是因式分解.
- A. (a+3)(a-3)=a2-9
- B. m2-4=(m+2)(m-2)
- C. a2-b2+1=(a+b)(a-b)+1
- D. 2πhr2=2π(r2h)
5.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
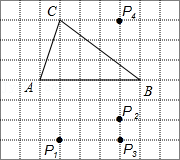

- A. 1个
- B. 2个
- C. 3个
- D. 4个
6.如图所示的网格是正方形网格,则∠PAB+∠PBA=( )°(点A,B,P是网格交点).
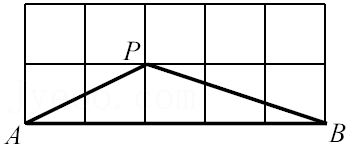

- A. 30
- B. 45
- C. 60
- D. 75
7.当x= 时,分式
的值为零.
| x2-1 |
| x-1 |
8.将一副三角板按如图所示的方式叠放,∠1=30°,∠2=45°,则∠3= °.
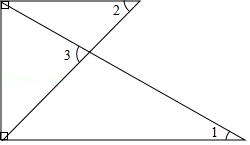

9.正多边形的每个内角都是160°,则它的边数是 .
10.已知△ABC中,AB=13,AC=20,BC边上的高AD=12,则BC的长为 .
11.若2x-5y=3,则代数式4+4x-10y的值是 .
12.如图,点A1,A2,A3…,An在x轴正半轴上,点C1,C2,C3,…,Cn在y轴正半轴上,点B1,B2,B3,…,Bn在第一象限角平分线OM上,OB1=B1B2=B2B3=…=Bn-1Bn=
a,A1B1⊥B1C1,A2B2⊥B2C2,A3B3⊥B3C3,…,AnBn⊥BnCn,…,则第n个四边形OAnBnCn的面积是 .
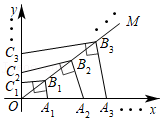
√3 |
| 2 |

13.计算:
(1)
(2)解方程:
+1=
.
(1)
√8
+√18
-√32
.(2)解方程:
| 2x |
| x-2 |
| 5 |
| 2-x |
14.分解因式:
(1)x3-9x;
(2)-2a3+12a2-10a.
(1)x3-9x;
(2)-2a3+12a2-10a.
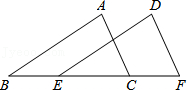
15.如图,点B,E,C,F在一条直线上,AC∥DF,BE=CF,∠A=∠D.求证:AB=DE.

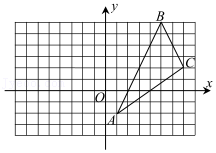
16.如图,在平面直角坐标系xOy中,A(1,-2).
(1)作△ABC关于y轴的对称图形△A′B′C′;
(2)写出B′和C′的坐标;
(3)求△ABC的面积.
(1)作△ABC关于y轴的对称图形△A′B′C′;
(2)写出B′和C′的坐标;
(3)求△ABC的面积.

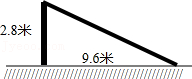
17.如图,一次“台风”过后,一根旗杆被台风从离地面2.8米处吹断裂,倒下的旗杆的顶端落在离旗杆底部9.6米处,那么这根旗杆被吹断裂前有多高?(旗杆粗细、断裂磨损忽略不计)

18.已知a+b=5,ab=
.
(1)求a2+b2的值;
(2)求a-b的值.
| 9 |
| 4 |
(1)求a2+b2的值;
(2)求a-b的值.
19.复习备考时,王老师在黑板上写了一道分式化简题的正确计算结果,随后用手遮住了原题目的一部分,如图:
( -a+1)÷
-a+1)÷
=-
(1)求被手遮住部分的代数式,并将其化简;
(2)原代数式的值能等于3吗?请说明理由.
(
 -a+1)÷
-a+1)÷| a2+4a+4 |
| a+1 |
| a-2 |
| a+2 |
(1)求被手遮住部分的代数式,并将其化简;
(2)原代数式的值能等于3吗?请说明理由.
20.如图,在△ABC中,BA=BC,CD和BE是△ABC的两条高,∠BCD=45°,BE与CD交于点H.
(1)求证:△BDH≌△CDA;
(2)求证:BH=2AE.

(1)求证:△BDH≌△CDA;
(2)求证:BH=2AE.

21.列方程解应用题:
老舍先生曾说“天堂是什么样子,我不晓得,但从我的生活经验去判断,北平之秋便是天堂.”(摘自《住的梦》)金黄色的银杏叶为北京的秋增色不少.
(1)小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树.他先让爸爸开车驶过这段公路,发现速度为60千米/小时,走了约3分钟,由此估算这段路长约 千米.
然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米.小宇计划从路的起点开始,每a米种一棵树,绘制示意图如下:

(2)考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵树,请你求出a的值.
老舍先生曾说“天堂是什么样子,我不晓得,但从我的生活经验去判断,北平之秋便是天堂.”(摘自《住的梦》)金黄色的银杏叶为北京的秋增色不少.
(1)小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树.他先让爸爸开车驶过这段公路,发现速度为60千米/小时,走了约3分钟,由此估算这段路长约 千米.
然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米.小宇计划从路的起点开始,每a米种一棵树,绘制示意图如下:

(2)考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵树,请你求出a的值.
22.已知a满足|2019-a|+
(1)
(2)根据(1)的分析,求a-20192的值.
√a-2020
=a.(1)
√a-2020
有意义,a的取值范围是 ;则在这个条件下将|2019-a|去掉绝对值符号可得|2019-a|= (2)根据(1)的分析,求a-20192的值.
23.新定义:在△ABC中,若存在一个内角是另外一个内角度数的n倍(n为大于1的正整数),则称△ABC为n倍角三角形.例如,在△ABC中,∠A=80°,∠B=60°,∠C=40°,可知∠A=2∠C,所以△ABC为2倍角三角形.
(1)在△DEF中,∠E=40°,∠F=35°,则△DEF为 倍角三角形.
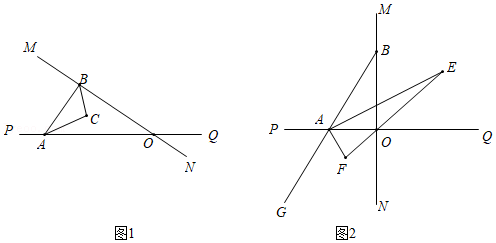
(2)如图1,直线MN与直线PQ相交于O,∠POM=30°,点A、点B分别是射线OP、OM上的动点;已知∠BAO、∠OBA的角平分线交于点C,在△ABC中,如果有一个角是另一个角的2倍,请求出∠BAC的度数.
(3)如图2,直线MN⊥直线PQ于点O,点A、点B分别在射线OP、OM上,已知∠BAO、∠OAG的角平分线分别与∠BOQ的角平分线所在的直线交于点E、F,若△AEF为3倍角三角形,试求∠ABO的度数.
(1)在△DEF中,∠E=40°,∠F=35°,则△DEF为 倍角三角形.
(2)如图1,直线MN与直线PQ相交于O,∠POM=30°,点A、点B分别是射线OP、OM上的动点;已知∠BAO、∠OBA的角平分线交于点C,在△ABC中,如果有一个角是另一个角的2倍,请求出∠BAC的度数.
(3)如图2,直线MN⊥直线PQ于点O,点A、点B分别在射线OP、OM上,已知∠BAO、∠OAG的角平分线分别与∠BOQ的角平分线所在的直线交于点E、F,若△AEF为3倍角三角形,试求∠ABO的度数.





