试卷题目
1.下面图案中,是轴对称图形的是( )
- A.

- B.

- C.

- D.

2.△ABC中,如果∠A+∠B=∠C,那么△ABC形状是( )
- A. 锐角三角形
- B. 直角三角形
- C. 钝角三角形
- D. 不能确定
3.若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( )
- A. 1
- B. 2
- C. 3
- D. 8
4.从一个多边形的顶点出发,可以作2条对角线,则这个多边形的内角和是( )
- A. 180°
- B. 270°
- C. 360°
- D. 540°
5.如图所示,在△ABC中,AD平分∠BAC交BC于点D,∠B=30°,∠ADC=70°,则∠BAC的度数是( )
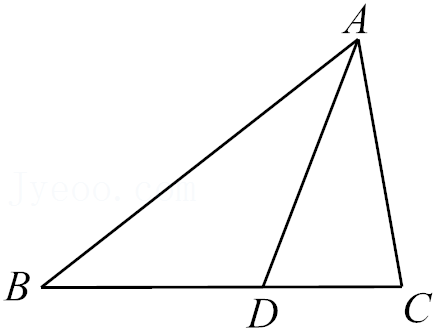

- A. 50°
- B. 60°
- C. 70°
- D. 80°
6.如图,△ABC≌△BAD,如果AB=6cm,BD=4cm,AD=5cm,那么BC的长是( )

- A. 4cm
- B. 5cm
- C. 6cm
- D. 无法确定
7.如图,BE=CF,AB∥DE,添加下列哪个条件不能证明△ABC≌△DEF的是( )

- A. AB=DE
- B. ∠A=∠D
- C. AC=DF
- D. AC∥DF
8.如图,AD为△ABC的高,E为AC上一点,BE交AD于点F,且有BF=AC,FD=CD,则△BFD≌△ACD的理由根据是( )
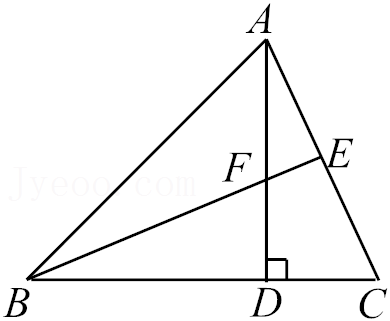

- A. SSS
- B. SAS
- C. ASA
- D. HL
9.如图所示,在△ABC中,D、E、F分别为BC、AD、CE的中点,且S△ABC=16cm2,则△DEF的面积等于( )
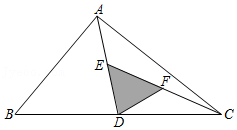

- A. 2cm2
- B. 4cm2
- C. 6cm2
- D. 8cm2
10.如图,在等边△ABC中,D、E分别在BC、AC上,且BD=CE,AD与BE相交于点P,则∠APE的度数是( )
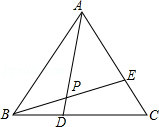

- A. 45°
- B. 55°
- C. 60°
- D. 75°
11.如图,把手机放在一个支架上面,可以使它稳固起来,这是利用了三角形的 .


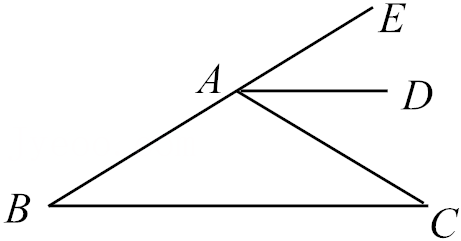
12.如图,AD是△ABC的外角∠EAC的平分线,AD∥BC,∠B=32°,则∠C的度数是 .

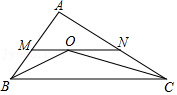
13.如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为 .

14.如图,已知等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则∠EFD= .
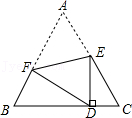

15.如图,坐标系中四边形ABCO是正方形,D是边OC上一点,E是正方形边上一点.已知B(-3,3),D(0,1),当AD=CE时,点E坐标为 .
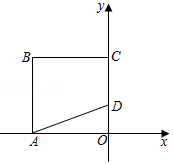

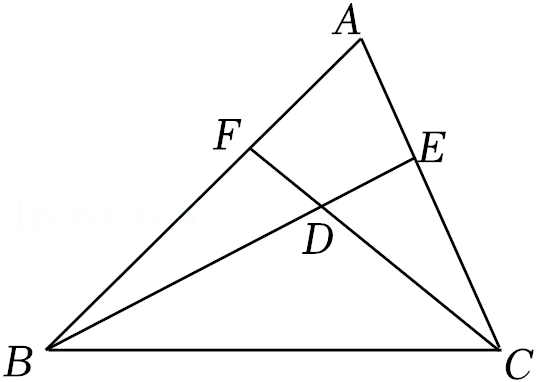
16.已知,如图,在△ABC中,点E,F分别为AC,AB边上的动点,BE和CF相交于点D,∠A=80°.
(1)如果BE,CF分别为AC,AB上的高线时,求∠BDC的度数;
(2)如果BE,CF分别平分∠ABC,∠ACB时,求∠BDC的度数.
(1)如果BE,CF分别为AC,AB上的高线时,求∠BDC的度数;
(2)如果BE,CF分别平分∠ABC,∠ACB时,求∠BDC的度数.

17.已知△ABC为等腰三角形,请解答下列问题:
(1)若此三角形的一个内角为100°,求其余两角的度数;
(2)若该三角形两边长为2和4,求此三角形的周长.
(1)若此三角形的一个内角为100°,求其余两角的度数;
(2)若该三角形两边长为2和4,求此三角形的周长.
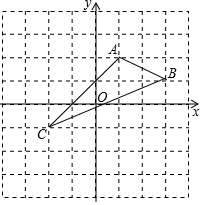
18.如图,在平面直角坐标系中,A(1,2)、B(3,1)、C(-2,-1)
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出A1、B1、C1的坐标;
(3)求△A1B1C1的面积.
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出A1、B1、C1的坐标;
(3)求△A1B1C1的面积.

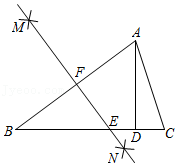
19.如图,在△ABC中,分别以A,B为圆心,以大于
AB的长为半径画弧,两弧交于M,N两点,直线MN交AB于点F,D为线段CE的中点,BE=AC.
(1)求证:AD⊥BC;
(2)若∠BAC=72°,求∠B的度数.
| 1 |
| 2 |
(1)求证:AD⊥BC;
(2)若∠BAC=72°,求∠B的度数.

20.如图,在Rt△ABC中,∠ACB=90°,D是AB边上的一点,过D作DE⊥AB交AC于点E,BC=BD,连接CD交BE于点F.
(1)求证:BE是CD的垂直平分线;
(2)若点D为AB的中点,且FE=1,求AC的长.
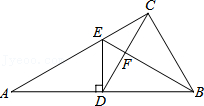
(1)求证:BE是CD的垂直平分线;
(2)若点D为AB的中点,且FE=1,求AC的长.

21.如图,点E是线段BC上除点C,B外的任意一点,分别以EC,BE为边在线段CB的同侧作等边△ABE和等边△DEC,AC交BD于F,交DE于N,BD交AE于M.
(1)求∠AFB的度数;
(2)连接MN,下列结论中正确的是 (把正确的序号直接填在横线上).
①△DME≌△CNE;②AN=BM;③MN∥BC;④MD=CD.

(1)求∠AFB的度数;
(2)连接MN,下列结论中正确的是 (把正确的序号直接填在横线上).
①△DME≌△CNE;②AN=BM;③MN∥BC;④MD=CD.

(1)①如图1,△ABC是等腰直角三角形,∠C=90o,点D为AB中点,则△AED∽ ;
②如图2,△ABC为正三角形,BD=CF,∠EDF=60°,则△BDE≌ ;
③如图3,正方形ABCD的顶点B在直线l上,分别过点A、C作AE⊥l于E,CF⊥l于F.若AE=1,CF=2,则EF的长为 .
【模型应用】
(2)如图4,将正方形OABC放在平面直角坐标系中,点O为原点,点A的坐标为(1,
√3
),则点C的坐标为 .【模型变式】
(3)如图5所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于D,DE=4cm,AD=6cm,求BE的长.






