试卷题目
1.已知x1,x2是方程2x2+
√5
x-2=0的两个实数根,则x12+x22的值是( )- A. -
3 4 - B. 1
- C.
13 4 - D. 9
2.实数a,b在数轴上对应点的位置如图所示,化简|a|+
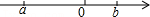
√(a-b)2
的结果是( )
- A. -2a+b
- B. 2a-b
- C. -b
- D. b
3.化简二次根式
√-8a3
的结果为( )- A. -2a√-2a
- B. 2a√2a
- C. 2a√-2a
- D. -2a√2a
4.化简:
√x2-6x+9
-(√3-x
)2=( )- A. 2x-6
- B. 0
- C. 6-2x
- D. 2x+6
5.已知
√3a+4
+b2-12b+36=0,则ab的值为( )- A. 4
- B. -4
- C. -8
- D. 8
6.用配方法解一元二次方程2x2-4x=5的过程中,配方正确的是( )
- A. (x-1)2=
7 2 - B. (x+1)2=
7 2 - C. (x+1)2=
5 2 - D. (x+1)2=
5 2
7.如果
,那么x的取值范围是( )
√
=| x-1 |
| x-3 |
√x-1 |
√x-3 |
- A. 1≤x≤3
- B. 1<x≤3
- C. x≥3
- D. x>3
8.如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为3,则△BCD的面积为( )
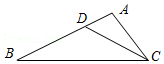

- A. 12
- B. 9
- C. 6
- D. 3
9.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
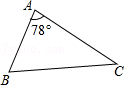

- A.

- B.

- C.

- D.

10.如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
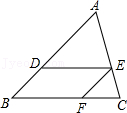

- A. 6
- B. 8
- C. 10
- D. 12
11.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,则四边形ABCD与四边形A′B′C′D′的面积比为( )
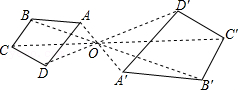

- A. 4:9
- B. 2:5
- C. 2:3
- D. √2:√3
12.如图,在▱ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①
=
;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中一定正确的是( )
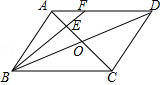
| AF |
| FD |
| 1 |
| 2 |

- A. ①②③④
- B. ①④
- C. ②③④
- D. ①②③
13.若
=
,则
= .
| a |
| 2a-b |
| 2 |
| 3 |
| b |
| a |
14.若
√27
与最简二次根式√2a-5
是同类二次根式,则a= .15.将4个数a,b,c,d排成2行、2列,两边各加一条竖直线记成
,定义
=ad-bc,上述记号就叫2阶行列式.若
=6,则x= .
| { |
|
| { |
|
| { |
|
16.某公司在2012年的盈利额为200万元,预计2014年的盈利额将达到242万元.若每年比上一年盈利额增长的百分率相同,那么该公司在2013年的盈利额为 万元.
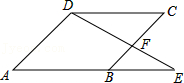
17.如图,E为▱ABCD的边AB延长线上的一点,且BE:AB=2:3,△BEF的面积为4,则▱ABCD的面积为 .

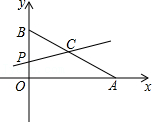
18.如图,平面直角坐标系中,已知点A(8,0)和点B(0,6),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点P的坐标是 .

19.计算下列各题:
(1)
(2)
+(3+
(1)
√45
÷(| 3 |
| 4 |
√
)×| 1 |
| 5 |
| 1 |
| 4 |
√2
;| 2 |
| 3 |
(2)
√18 +√2 |
√2 |
√2
)2.20.解方程:
(1)2x2-4x-9=0(用配方法解)
(2)3x2-4
(1)2x2-4x-9=0(用配方法解)
(2)3x2-4
√3
x+2=0(用公式法解)21.某湿地风景区特色旅游项目:水上游艇,旅游人员消费后风景区可盈利10元/人,每天消费人员为500人,为增加盈利,准备提高票价,经调查发现,在其他条件不变的情况下,票价每涨1元,消费人员就减少20人.现该项目要保证每天盈利6000元,同时又要旅游者得到实惠,那么票价应涨价多少元?
22.如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,交DE于点H,AM⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=4,AB=6,求
的值.

(1)求证:△ADE∽△ABC;
(2)若AD=4,AB=6,求
| FH |
| GM |