试卷题目
1.下列四个选项中的数,不是分数的是( )
- A. √3
3 - B. 80%
- C. 2
1 3 - D.
22 7
2.对于①x-3xy=x(1-3y),②(x+3)(x-1)=x2+2x-3,从左到右的变形,表述正确的是( )
- A. 都是因式分解
- B. 都是乘法运算
- C. ①是因式分解,②是乘法运算
- D. ①是乘法运算,②是因式分解
3.下列各数中,化简结果为-2021的是( )
- A. -(-2021)
- B. √(2021)2
- C. |-2021|
- D. 3√-20213
4.若□×2xy=16x3y2,则□内应填的单项式是( )
- A. 4x2y
- B. 8x3y2
- C. 4x2y2
- D. 8x2y
5.如图,矩形内有两个相邻的正方形,面积分别是x2(x>0)和4,那么阴影部分的面积为( )
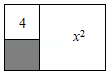

- A. 2x+4
- B. 2x-4
- C. x2-4
- D. 2x-2
6.复习课上,老师给出一个问题“已知等腰三角形的一边等于5,另一边等于6,求它的周长.”小华代表小组发言:“等腰三角形的边有两种,腰和底边,所以第一种情况5是腰长,6是底边长;第二种情况5是底边长、6是腰长,从而得最终结果为16或17.”小华的上述方法体现的数学思想是( )
- A. 公理化
- B. 分类讨论
- C. 数形结合
- D. 由特殊到一般
7.正方形面积为8,其边长是x,以下关于x的结论中,错误的是( )
- A. x是无理数
- B. 8的平方根是x
- C. 2<x<3
- D. 能够在数轴上找到表示实数x的点
8.下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容.
如图,已知AB=AD,CB=CD,∠B=30°,∠BAD=50°,求∠BCD的度数.
解:在△ABC和△ADC中,
,
∴△ABC≌△ADC(@).
∴∠BCA=∠DCA,∠BAC=(◎)=25°.
(全等三角形的■相等)
∵∠B=30°,∠BAC=25°,
∴∠BCA=180°-∠B-∠BAC=125°.
∴∠BCD=360°-2∠BCA=(※).
下面的作答正确的是( )

如图,已知AB=AD,CB=CD,∠B=30°,∠BAD=50°,求∠BCD的度数.
解:在△ABC和△ADC中,
| { |
|
∴△ABC≌△ADC(@).
∴∠BCA=∠DCA,∠BAC=(◎)=25°.
(全等三角形的■相等)
∵∠B=30°,∠BAC=25°,
∴∠BCA=180°-∠B-∠BAC=125°.
∴∠BCD=360°-2∠BCA=(※).
下面的作答正确的是( )

- A. @代表ASA
- B. ◎代表∠DCA
- C. ■代表对应边
- D. ※代表110°
9.对于实数a、b,定义一种运算:a*b=(a-b)2.给出三个推断:①a*b=b*a;②(a*b)2=a2*b2;③(-a)*b=a*(-b);其中正确的推断个数是( )
- A. 0
- B. 1
- C. 2
- D. 3
10.将从1开始的一组数按如下的规律排列:规定位于第m行第n列的数记为(m,n),例如
√15
记为(4,2),按此规律,√2021
记为( )| 行列 | 第1列 | 第2列 | 第3列 | 第4列 |
| 第1行 | 1 | √2 | √3 | 2 |
| 第2行 | 2 √2 | √7 | √6 | √5 |
| 第3行 | 3 | √10 | √11 | 2 √3 |
| 第4行 | 4 | √15 | √14 | √13 |
| … | … | … | … | … |
- A. (506,1)
- B. (506,4)
- C. (505,4)
- D. (505,1)
11.中国清代学者华衡芳与英国人傅兰雅合译的《代数学》卷首有“代数之法,无论何数,皆可以任何记号代之”,则2的算术平方根用符号表示为 .
12.现有甲、乙、丙三种不同的矩形纸片(边长如图).
(1)取甲、乙纸片各1块,其面积和为 ;
(2)嘉嘉要用这三种纸片紧密拼接成一个大正方形,先取甲纸片1块,再取乙纸片4块,还需取丙纸片 块.
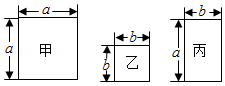
(1)取甲、乙纸片各1块,其面积和为 ;
(2)嘉嘉要用这三种纸片紧密拼接成一个大正方形,先取甲纸片1块,再取乙纸片4块,还需取丙纸片 块.

13.已知432=1849,442=1936,452=2025,462=2116.若n<
√2021
<n+1,则整数n的值为 .14.贾宪三角也叫杨辉三角,在欧洲也称为帕斯卡三角形,是中国古代数学的杰出研究成果之一,是一种离散型的数形结合.如图,是杨辉三角的一部分,它反映了二项式乘方展开式的系数规律,则图中第五行中的所有数字之和为 .


15.过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角度数为 .
16.化简:(1-2m)(2m+1)-(3+4m)(6-m).
17.计算或解方程:
(1)(-1.25)2021×(-
)2020;
(2)
(x+3)3=24.
(1)(-1.25)2021×(-
| 4 |
| 5 |
(2)
| 1 |
| 9 |
18.阅读下列材料
分解因式:4x-16x3
小云的做法:
原式=16x3-4x①
=4x(4x2-1)②
=4x(2x-1)(2x+1)③
小朵的做法:
原式=4x (1-4x2)①
=4x(1-4x) (1+4x)②
小天的做法:
原式=x (4-16x2)①
=x[22-(4x)2]②
=x(2-4x) (2+4x)③
请根据上述材料回答下列问题:
(1)小云的解题过程从 步出现错误的,错误的原因是: .小朵的解题过程从 步出现错误的,错误的原因是: .小天的解题过程从 步出现错误的,错误的原因是: .
(2)若都不正确,请你写出正确的解题过程.
分解因式:4x-16x3
小云的做法:
原式=16x3-4x①
=4x(4x2-1)②
=4x(2x-1)(2x+1)③
小朵的做法:
原式=4x (1-4x2)①
=4x(1-4x) (1+4x)②
小天的做法:
原式=x (4-16x2)①
=x[22-(4x)2]②
=x(2-4x) (2+4x)③
请根据上述材料回答下列问题:
(1)小云的解题过程从 步出现错误的,错误的原因是: .小朵的解题过程从 步出现错误的,错误的原因是: .小天的解题过程从 步出现错误的,错误的原因是: .
(2)若都不正确,请你写出正确的解题过程.
19.先化简,再求值:(2x+y)2+(x-y)(x+y)-5x(x-y),其中x=
√2
+1,y=√2
-1.20.如图,已知△ABC中,AB=AC,BD⊥AC,垂足为D,CE⊥AB,垂足为E.求证:BD=CE.









