试卷题目
1.在以下大众、东风、长城、奔驰四个汽车标志中,不是轴对称图形的是( )
- A.

- B.

- C.

- D.

2.下列长度的3条线段,能首尾依次相接组成三角形的是( )
- A. 1cm,2cm,4cm
- B. 8cm,6cm,4cm
- C. 12cm,5cm,6cm
- D. 1cm,3cm,4cm
3.如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )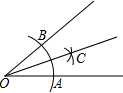

- A. SAS
- B. ASA
- C. AAS
- D. SSS
4.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )

- A. AB=AC
- B. ∠BAE=∠CAD
- C. BE=DC
- D. AD=DE
5.如图,在Rt△ABC中,∠B=45°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确的个数是( )个.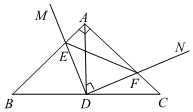

- A. 1
- B. 2
- C. 3
- D. 4
6.如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )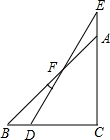

- A. 15°
- B. 25°
- C. 30°
- D. 10°
7.如图,在不等边△ABC中,PM⊥AB于点M,PN⊥AC于点N,且PM=PN,Q在AC上,PQ=QA,MP=3,△AMP的面积是6,下列结论:①AM<PQ+QN,②QP∥AM,③△BMP≌△PQC,④∠QPC+∠MPB=90°,⑤△PQN的周长是7,其中正确的有( )个.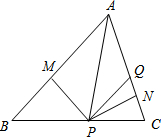

- A. 1
- B. 2
- C. 3
- D. 4
8.如图所示的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=( )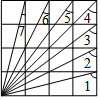

- A. 330°
- B. 315°
- C. 310°
- D. 320°
9.(1)两边和一角对应相等的两个三角形全等;(2)三个内角对应相等的两个三角形全等;(3)斜边对应相等的两个等腰直角三角形全等;(4)两边和第三边上的高对应相等的两个三角形全等.其中正确的个数为( )个.
- A. 1
- B. 2
- C. 3
- D. 4
10.如图是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )















