试卷题目
1.下列计算正确的是( )
- A. a2•a3=a5
- B. (a3)2=a5
- C. (2ab2)3=6a3b6
- D. 3a2÷4a2=a
3 4
2.若式子
+(x-4)0有意义,则实数x的取值范围是( )
| x |
| x-3 |
- A. x≠3
- B. x≠4
- C. x≠3或x≠4
- D. x≠3且x≠4
3.华为Mate20手机搭载了全球首款7纳米制程芯片,7纳米就是0.000000007米.数据0.000000007用科学记数法表示为( )
- A. 7×10-7
- B. 0.7×10-8
- C. 7×10-8
- D. 7×10-9
4.一个多边形的内角和是外角和的2倍,这个多边形是( )
- A. 三角形
- B. 四边形
- C. 五边形
- D. 六边形
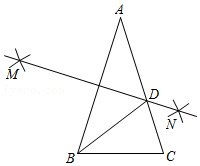
5.如图,已知AB=AC,AB=8,BC=5,以A,B两点为圆心,大于
AB的长为半径画弧,两弧相交于点M,N,连接MN与AC相交于点D,连接BD,则△BDC的周长为( )
| 1 |
| 2 |

- A. 8
- B. 10
- C. 11
- D. 13
6.已知x2+kxy+64y2是一个完全平方式,则k的值是( )
- A. 8
- B. ±8
- C. 16
- D. ±16
7.如图所示,下列结论正确的是( )
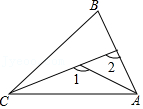

- A. ∠1>∠B>∠2
- B. ∠B>∠2>∠1
- C. ∠2>∠1>∠B
- D. ∠1>∠2>∠B
8.某单位向一所希望小学赠送1080本课外书,现用A、B两种不同的包装箱进行包装,单独使用B型包装箱比单独使用A型包装箱可少用6个;已知每个B型包装箱比每个A型包装箱可多装15本课外书.若设每个A型包装箱可以装书x本,则根据题意列得方程为( )
- A. =
1080 x +61080 x-15 - B. =
1080 x -61080 x-15 - C. =
1080 x+15 -61080 x - D. =
1080 x+15 +61080 x
9.如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
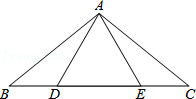

- A. BD=CE
- B. AD=AE
- C. DA=DE
- D. BE=CD
10.如图,在第1个△A1BC中,∠B=30°,A1B=CB,在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E…按此做法继续下去,则第2021个三角形中以A2021为顶点的内角度数是( )
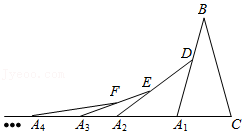

- A. ()2019•75°
1 2 - B. ()2020•75°
1 2 - C. ()2021•75°
1 2 - D. ()2025•75°
1 2
11.计算:(-
)-2-(-1)2021-(π-2)0= .
| 1 |
| 3 |
12.在△ABC中,∠A=∠B,∠A+∠C=3∠B,则△ABC的形状是 .
13.在平面直角坐标系中,若点M(2a-7,2)和点N(-3-b,a+b)关于y轴对称,则ab= .
14.借助如图所示的“三等分角仪”能三等分某度数的角,这个“三等分角仪”由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动.若∠BDE=60°,则∠CDE= °.


15.已知一张三角形纸片ABC(如图甲),其中∠ABC=∠C.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠ABC的大小为 °.












