2024-2025学年八年级数学上册同步培优讲义及知识清单
第2章《轴对称图形》
【知识清单】
考点一、轴对称
1.轴对称图形和轴对称
(1)轴对称图形
如果一个图形沿着某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.轴对称图形的性质:轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
(2)轴对称
定义:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴.成轴对称的两个图形的性质:
①关于某条直线对称的两个图形形状相同,大小相等,是全等形;
②如果两个图形关于某条直线对称,则对称轴是任何一对对应点所连线段的垂直平分线;
③两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么它们的交点在对称轴上.
(3)轴对称图形与轴对称的区别和联系
区别:轴对称是指两个图形的位置关系,轴对称图形是指具有特殊形状的一个图形;轴对称涉及两个图形,而轴对称图形是对一个图形来说的联系:如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条轴对称;如果把成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形.
2.线段的垂直平分线
线段的垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等.反过来,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
【例1】山东省第二十七届运动会将于2024年8月25日在日照市开幕,“全民健身与省运同行”成为日照市当前的运动主题.在下列给出的运动图片中,是轴对称图形的是( )
【答案】D
解:A、不是轴对称图形,故本选项不符合题意;B、不是轴对称图形,故本选项不符合题意;C、不是轴对称图形,故本选项不符合题意;D、是轴对称图形,故本选项符合题意.
故选:D.
【变式1】如图,△ABC与△AED关于直线l对称,若∠B=30°,∠C=95°,则∠DAE=( )
- 30° B.95° C.55° D.65°
【答案】C
【变式2】如图,由四个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点.在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有( )
A.1个 B.2个 C.3个 D.4个
【答案】C;
【解析】先把田字格图标上字母如图,确定对称轴找出符合条件的三角形,再计算个数.△HEC与△ABC关于CD对称;△FDB与△ABC关于BE对称;△GED与△ABC关于HF对称;关于AG对称的是它本身.所以共3个.
【例2】如图所示,∠AOB内有一点P,P1,P2分别是点P关于OA,OB的对称点,P1P2交OA于点M,交OB于点N,若P1P2=5cm,求△PMN的周长.
【答案】5cm
解:∵P与P1关于OA对称,∴OA为线段PP1的垂直平分线,∴MP=MP1,
同理,P与P2关于OB对称,∴OB为线段PP2的垂直平分线,∴NP=NP2
∴△PMN的周长为5cm.
【变式】如图,点E是△ABC的边AB的延长线上一点,∠BCE=∠A+∠ACB,求证:点E在BC的垂直平分线上.
证明:∵∠BCE=∠A+∠ACB,∠EBC=∠A+∠ACB,∴∠BCE=∠EBC,∴BE=CE,
∴点E在BC的垂直平分线上.
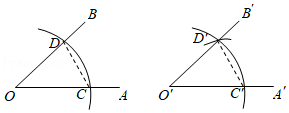
【例3】如图所示,P为△BOA内任一点,在OB上找一点M,在OA上找一点N,使得△PMN的周长最短.
解:如图.作点P关于OA、OB的对称点P”、P‘,连接P‘P”,分别交OA、OB于点N、M,即M、N为所求.此时△PMN的周长为PM+PN+MN=P”N+MN+P‘M≥P‘P”,即最小值为P‘P”的长度.
【变式】 如图,在所给的平面直角坐标系中,正方形网格单位长是1,△ABC的顶点都在格点上.
(1)已知A(﹣5,0),B(﹣1,0),C(﹣3,2),作出△ABC关于y轴对称的△A‘B‘C,并写出点A‘,B‘,C′的坐标.
(2)在y轴上向出点P,使PA+PC最小.
(3)在(1)的条件,在y轴上画出点M,使|MB‘﹣MC′|最大.
【答案】(1)图见分析,A‘(5,0),B‘(1,0),C′(3,2).(2)见分析(3)见分析
(1)解:如图,△A‘B‘C,A‘(5,0),B‘(1,0),C′(3,2).
(2)如图,点P即为所求;
(3)点M即为所求.
考点二、作轴对称图形
1.作轴对称图形
(1)几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接这些点,就可以得到原图形的轴对称图形;
(2)对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
2.用坐标表示轴对称
点(x,y)关于x轴对称的点的坐标为(x,-y);点(x,y)关于y轴对称的点的坐标为(-x,y);点(x,y)关于原点对称的点的坐标为(-x,-y).
【例4】如图所示,在正方形网格中,每个小正方形的边长为1个单位.
(1)过直线m作四边形ABCD的对称图形;
(2)求四边形ABCD的面积.
【答案】(1)见分析;(2)8
解:(1)如图所示:
【变式1】已知△ABC在平面直角坐标系中的位置如图所示:
- 画出△ABC关于y轴对称的△AB1C1;并写出B1的坐标;
- 将△ABC向右平移8个单位,画出平移后的△A1B2C2,并写出B2的坐标;
- 在(1)、(2)的基础上,写出△AB1C1与△A1B2C2有怎样的位置关系?
- 在y轴上有一点P,使得PB+PC最小,请画出点P;(用虚线保留画图的痕迹)
- 在y轴上有一点Q,使得QB-QC最大,请画出点Q.(用虚线保留画图的痕迹)
【答案】(1)作图见分析,B1(3,2)(2)作图见分析,B2(5,2);
(3)由图可知△AB1C1与△A1B2C2关于直线x=4对称;(4)作图见分析(5)作图见分析
解:(1)作图见分析,B1(3,2)
(2)作图见分析,B2(5,2);
(3)由图可知△AB1C1与△A1B2C2关于直线x=4对称;
(4)作图见分析
连接BC1,交y轴于点P,连接BC,
∵PC1=PC,PC+PB=PC1+PB≥BC1
当B,P,C1三点共线时,PB+PC最小
(5)作图见分析
延长BC交y轴于点Q,∵QB–QC≤BC
当B,C,Q三点共线时,取得最大值
【例5】如图,△ABC关于平行于x轴的一条直线对称,已知A点坐标是(1,2),C点坐标是(1,-4),则这条平行于x轴的直线是( )
A.直线x=-1 B.直线x=-3 C.直线y=-1 D.直线y=-3
【答案】C;
【解析】
解:由题意可知,该条直线垂直平分线段AC
又A点坐标是(1,2),C点坐标是(1,-4),∴AC=6,∴点A,C到该直线的距离都为3,即可得直线为y=-1
【变式1】如图,若直线m经过第二、四象限,且平分坐标轴的夹角,Rt△AOB与Rt△A’OB’关于直线m对称,已知A(1,2),则点A’的坐标为( )
A.(-1,2) B.(1,-2) C.(-1,-2) D.(-2,-1)
【答案】D;
提示:因为Rt△AOB与Rt△A’OB’关于直线m对称,所以通过作图可知,A’的坐标是(-2,-1).
【变式2】如图,ΔABC中,点A的坐标为(0,1),点C的坐标为(4,3),点B的坐标为(3,1),如果要使ΔABD与ΔABC全等,求点D的坐标.
【答案】
解:满足条件的点D的坐标有3个(4,-1);(-1,-1);(-1,3).
考点三、等腰三角形
1.等腰三角形
(1)定义:有两边相等的三角形,叫做等腰三角形.
(2)等腰三角形性质
①等腰三角形的两个底角相等,即“等边对等角”;
②等腰三角形顶角的平分线、底边上的中线与底边上的高线互相重合(简称“三线合一”).特别地,等腰直角三角形的每个底角都等于45°.
(3)等腰三角形的判定
如果一个三角形有两个角相等,那么这两个角所对的边也相等(即“等角对等边”).
2.等边三角形
(1)定义:三条边都相等的三角形,叫做等边三角形.
(2)等边三角形性质:等边三角形的三个角相等,并且每个角都等于60°.
(3)等边三角形的判定:
①三条边都相等的三角形是等边三角形;
②三个角都相等的三角形是等边三角形;
③有一个角为 60°的等腰三角形是等边三角形.
3.直角三角形的性质定理:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
【例6】如图,已知∠B=∠C,DE⊥AB于点E, DF⊥AC于点F,且BE=CF.求证:
(1)AD是∠BAC的平分线;
(2)AE=AF.
(1)证明:∵DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=90°,
在△BDE与△CDF中,∠B=∠C,BE=CF,∠DEB=∠DFC,
∴△BDE≌△CDF(ASA),∴BD=CD,∴AD是△ABC的中线,
∵∠B=∠C,∴AB=AC,∴AD是∠BAC的平分线;
(2)证明:∵∠B=∠C,∴AB=AC,
∵BE=CF,∴AB–BE=AC–CF,即AE=AF.