试卷题目
1.下列交通标志中,是轴对称图形的是( )
- A.
 向左转弯
向左转弯 - B.
 直行和向右转弯
直行和向右转弯 - C.
 直行
直行 - D.
 环岛行驶
环岛行驶
2.若最简二次根式
√a+1
与最简二次根式√2a
是同类二次根式,则a的值是( )- A. a=1
- B. a=-1
- C. a=2
- D. a=-2
3.下列分式中最简分式是( )
- A.
2x+4 6x+8 - B.
x+y x2-y2 - C.
x2+y2 x+y - D.
x2-y2 x2-2xy+y2
4.将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )
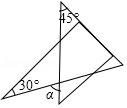

- A. 45°
- B. 60°
- C. 75°
- D. 85°
5.下列事件中,属于随机事件的是( )
- A. 用长度分别是1cm,2cm,3cm的细木条首尾顺次相连可组成一个三角形
- B. 用长度分别是3cm,4cm,5cm的细木条首尾顺次相连可组成一个直角三角形
- C. 如果一个三角形有两个角相等,那么两个角所对的边也相等
- D. 有两组对应边和一组对应角分别相等的两个三角形全等
6.等腰三角形的一个角是70°,则它的一个底角的度数是( )
- A. 70°
- B. 70°或55°
- C. 80°
- D. 55°
7.下列命题是假命题的是( )
- A. 直角三角形两锐角互余
- B. 有三组对应角相等的两个三角形全等
- C. 两直线平行,同位角相等
- D. 角平分线上的点到角两边的距离相等
8.如图,五根小木棒,其长度分别为5,9,12,13,15,现将它们摆成两个直角三角形,其中正确的是( )
- A.

- B.

- C.

- D.

9.若分式
的值为0,则x的值等于 .
| x-1 |
| 2x+1 |
10.16的算术平方根是 .
11.如图,∠C=∠D=90°,AC=AD,请写出一个正确的结论 .


12.比较大小:2
√2
3(填“>”、“ =”或“<” ).13.只有1和它本身两个因数且大于1的自然数叫做质数,我国数学家陈景润在有关质数的“哥德巴赫猜想”的研究中取得了世界领先的成果.从3,5,7,11,13,23这6个质数中随机抽取一个,则抽到个位数是3的可能性是 .
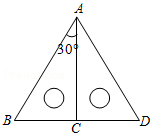
14.如图,将两个含30°角的全等的三角尺摆放在一起,可以证得△ABD是等边三角形,于是我们得到:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半如果BC=2,那么点C到AB的距离为 .

15.已知a,b是有理数,且满足(ab-2)2+
√b+1
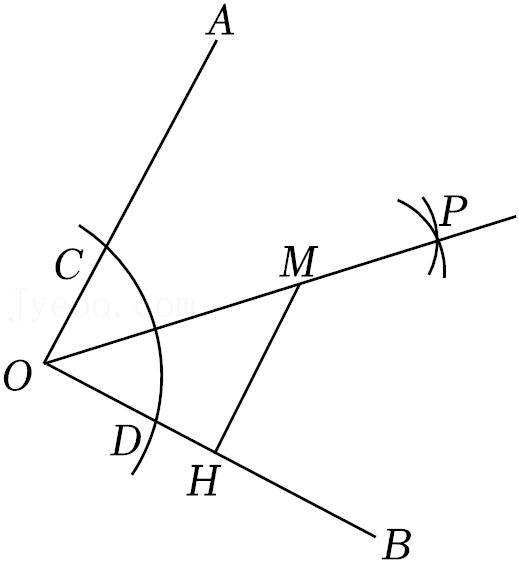
=0,那么a= ,b= .16.如图,∠AOB=90°,按以下步骤作图:
①以O为圆心,任意长为半径作弧,交OA于C,交OB于D;
②分别以C、D为圆心,以大于
CD的同样长为半径作弧,两弧交于点P;
③作射线OP.
如图,点M在射线OP上,过M作MH⊥OB于H,若MH=2,则OM= .
①以O为圆心,任意长为半径作弧,交OA于C,交OB于D;
②分别以C、D为圆心,以大于
| 1 |
| 2 |
③作射线OP.
如图,点M在射线OP上,过M作MH⊥OB于H,若MH=2,则OM= .

17.计算:
√12
+(3.14-π)0-3√27
+|√3
-2|18.计算:
√8
×√2
+(√2
-1)219.计算:(
-1)÷
| 1 |
| a-1 |
| a2-2a |
| a2-2a+1 |
20.已知,∠A=∠D,BC平分∠ABD,求证:AC=DC.

21.解分式方程:
(1)
=
;
(2)1+
=
.
(1)
| 2 |
| x-1 |
| 1 |
| x+1 |
(2)1+
| 6 |
| x2-9 |
| x |
| x-3 |
22.已知:如图△ABC
求作:点P,使得点P在AC上,且PC=PB.
作法:
①分别以B,C为圆心,大于
BC的同样长为半径作弧,两弧分别交于M,N;
②作直线MN,与AC交于P点,与BC交于H.
(1)利用直尺和圆规依做法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵BM=CM,BN=CN,
∴M、N在线段BC的垂直平分线上.( )(填推理的依据)
即MN是AB的垂直平分线.
∴点P在直线MN上.
∴PC=PB.( )(填推理的依据)
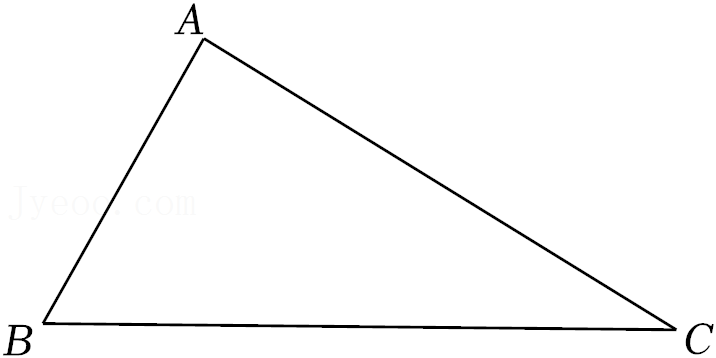
求作:点P,使得点P在AC上,且PC=PB.
作法:
①分别以B,C为圆心,大于
| 1 |
| 2 |
②作直线MN,与AC交于P点,与BC交于H.
(1)利用直尺和圆规依做法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵BM=CM,BN=CN,
∴M、N在线段BC的垂直平分线上.( )(填推理的依据)
即MN是AB的垂直平分线.
∴点P在直线MN上.
∴PC=PB.( )(填推理的依据)

23.先化简,再代入求值:
•(
+x-4),其中x2-2x-2=0.
| x2 |
| x-2 |
| 4 |
| x |
24.在《开学第一课》中,东京奥运会的奥运健儿们向新开学的同学们送上了“希望你们能像运动员一样,努力奔跑,刻苦学习,实现你们的梦想”的祝福.为了提高学生的体育锻炼的意识和能力,丰富学生的体育锻炼的内容,学校准备购买一批体育用品.在购买跳绳时,甲种跳绳比乙种跳绳的单价低10元,用1600元购买甲种跳绳与用2100元购买乙种跳绳的数量相同,求甲乙两种跳绳的单价各是多少元?
25.已知数a,b,c在数轴上的位置如图所示:
化简:

化简:
√b2
-|a-b|+√(c-a)2
-|c|.
26.针对于等腰三角形三线合一的这条性质,老师带领同学们做了进一步的猜想和证明,提问:如果一个三角形中,一个角的平分线和它所对的边的中线重合,那么这个三角形是等腰三角形.
已知:在△ABC中,AD平分∠CAB,交BC边于点D,且CD=BD,求证:AB=AC.
以下是甲、乙两位同学的做法.
甲:根据角平分线和中线的性质分别能得出一组角等和一组边等,再加一组公共边,可证△ACD≌△ABD,所以这个三角形为等腰三角形;
乙:延长AD到E,使DE=AD,连接BE,可证△ACD≌△EBD,依据已知条件可推出AB=AC,所以这个三角形为等腰三角形.
(1)对于甲、乙两人的做法,下列判断正确的是 ;
A.两人都正确 B.甲正确,乙错误 C.甲错误,乙正确
(2)选择一种你认为正确的做法,并证明.
已知:在△ABC中,AD平分∠CAB,交BC边于点D,且CD=BD,求证:AB=AC.
以下是甲、乙两位同学的做法.
甲:根据角平分线和中线的性质分别能得出一组角等和一组边等,再加一组公共边,可证△ACD≌△ABD,所以这个三角形为等腰三角形;
乙:延长AD到E,使DE=AD,连接BE,可证△ACD≌△EBD,依据已知条件可推出AB=AC,所以这个三角形为等腰三角形.
(1)对于甲、乙两人的做法,下列判断正确的是 ;
A.两人都正确 B.甲正确,乙错误 C.甲错误,乙正确
(2)选择一种你认为正确的做法,并证明.

27.如图,在△ABC中,∠BAC=90°,AB=AC,点D直线BC上(与点B,C不重合),点D关于直线AC的对称点为点E,连接AD,AE,DE.
(1)如图1,当点D为线段BC的中点时,猜想:△ADE的形状并证明;
(2)当点D在线段BC的延长线上时,连接BE、CE、DE.
①根据题意在图2中补全图形;
②用等式表示线段BE、CD、BC的数量关系,并证明.
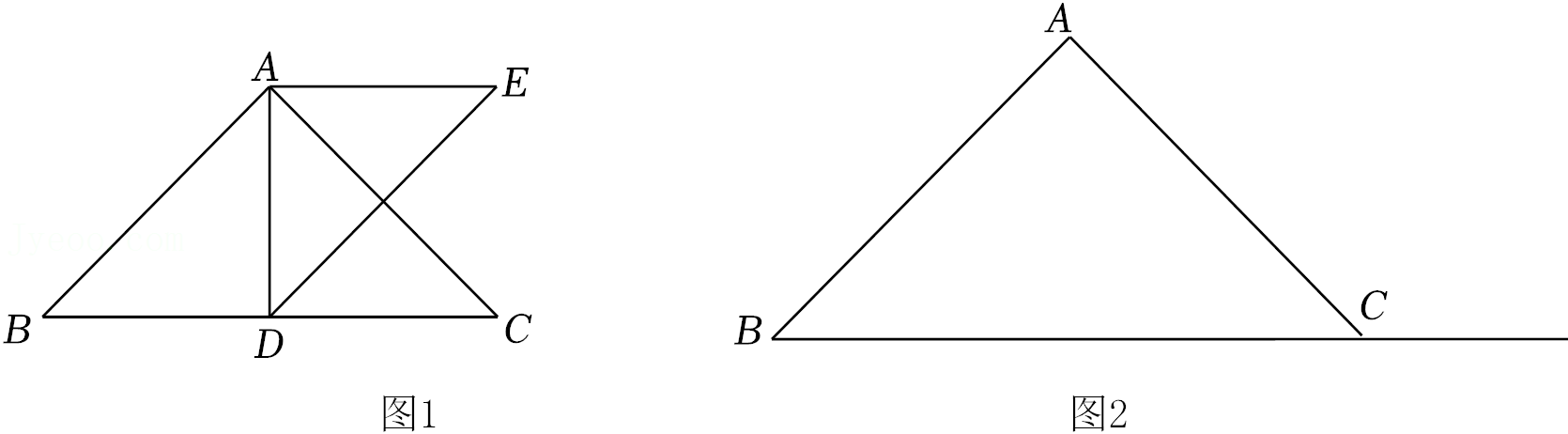
(1)如图1,当点D为线段BC的中点时,猜想:△ADE的形状并证明;
(2)当点D在线段BC的延长线上时,连接BE、CE、DE.
①根据题意在图2中补全图形;
②用等式表示线段BE、CD、BC的数量关系,并证明.

28.我们已经学过(x-a)(x-b)=x2-(a+b)x+ab,如果关于x的分式方程满足x+
=a+b(a,b分别为非零整数),且方程的两个跟分别为x1=a,x2=b.
我们称这样的方程为“十字方程”.
例如:x+
=3可化为x+
=1+2=3,∴x1=1,x2=2.
再如:x+
=-5可化为x+
=-2-3=-5,∴x1=-2,x2=-3.
应用上面的结论解答下列问题:
(1)“十字方程” x+
=-6,则x1= ,x2= ;
(2)“十字方程” x-
=-1的两个解分别为x1=a,x2=b,求
+
的值;
(3)关于x的“十字方程” x+
=2n+4的两个解分别为x1,x2(x1<x2),求
的值.
| ab |
| x |
我们称这样的方程为“十字方程”.
例如:x+
| 2 |
| x |
| 1×2 |
| x |
再如:x+
| 6 |
| x |
| (-2)×(-3) |
| x |
应用上面的结论解答下列问题:
(1)“十字方程” x+
| 8 |
| x |
(2)“十字方程” x-
| 2 |
| x |
| 1 |
| a |
| 1 |
| b |
(3)关于x的“十字方程” x+
| n2+n |
| x-3 |
| x2 |
| x1+1 |