试卷题目
1.以下历届冬奥会图标中,是中心对称图形的是( )
- A.

- B.

- C.

- D.

2.下列各式从左到右的变形是因式分解的是( )
- A. ab+bc+d=b(a+c)+d
- B. (a-3)(a+1)=a2-2a-3
- C. a2-ab=a(a-b)
- D. 6a2b=3ab•2a
3.在平面直角坐标系中,将点A(1,3)向右平移3个单位长度,得到的点A′的坐标为( )
- A. (-2,3)
- B. (4,3)
- C. (1,6)
- D. (1,0)
4.要使分式
有意义,x的取值应满足( )
| 2 |
| x-1 |
- A. x≠0
- B. x≠1
- C. x≠2
- D. x为任意实数
5.如图,将△AOB绕点O按逆时针方向旋转一定角度后得到△COD,旋转角是( )


- A. ∠AOB
- B. ∠BOC
- C. ∠COD
- D. ∠AOC
6.如图,▱ABCD的对角线AC与BD相交于点O,BD=8,则OB的长为( )
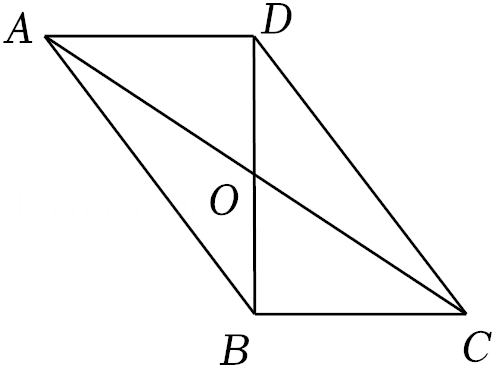

- A. 3
- B. 4
- C. 5
- D. 8
7.在下列分式的变形中,从左到右一定正确的是( )
- A. =
a b a+1 b+1 - B. =
2a 2b a b - C. =
a b a2 b2 - D. =
a b ac bc
8.如图,菱形ABCD中,∠A=50°,则∠ADB的度数为( )
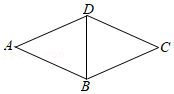

- A. 65°
- B. 55°
- C. 45°
- D. 25°
9.在冬奥会开幕式上,美丽的冬奥雪花呈现出浪漫空灵的气质.如图,雪花图案本身的设计呈现出充分的美感,它是一个中心对称图形.其实“雪花”图案也可以看成自身的一部分围绕图案的中心依次旋转一定角度得到的,这个角的度数可以是( )


- A. 30°
- B. 45°
- C. 60°
- D. 90°
10.为做好校园卫生防控,某校计划购买甲、乙两种品牌的消毒液.乙品牌消毒液每桶的价格比甲品牌每桶价格少25元,已知用2000元购买甲品牌的数量与用1500元购买乙品牌的数量相同.设甲品牌消毒液每桶的价格是x元,根据题意可列方程为( )
- A. =
2000 x 1500 x-25 - B. =
1500 x 2000 x+25 - C. =
1500 x+25 2000 x - D. =
1500 x 2000 x-25
11.如图,△ABC中,AB=10,AC=7,BC=9,点D、E、F分别是AB、AC、BC的中点,则四边形DBFE的周长是( )
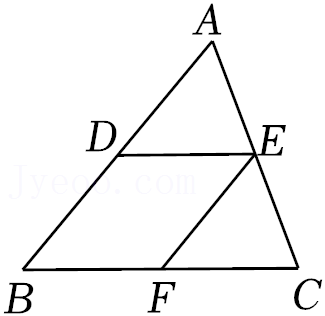

- A. 13
- B.
19 2 - C. 17
- D. 19
12.小颖用下面四个图形拼成一个大长方形,并据此写出了一个把某多项式因式分解的等式,这个等式是( )
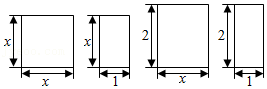

- A. x2+3x+2=(x+1)(x+2)
- B. x2-3x+2=(x-1)(x-2)
- C. (x+1)(x+2)=x2+3x+2
- D. x2+3x+2=x(x+3)+2
13.分解因式:a2-1= .
14.一个多边形的每个外角都是60°,则这个多边形边数为 .
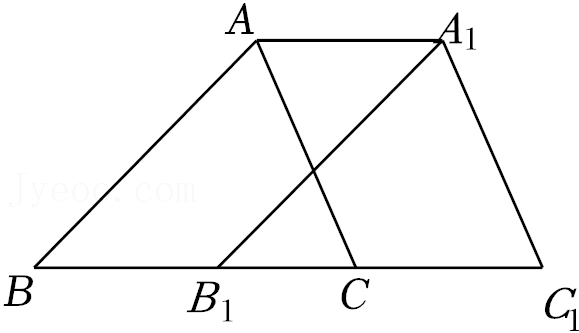
15.如图,将△ABC沿边BC的方向平移4个单位到△A1B1C1的位置,已知B1C=3,则线段BC的长为 .

16.若分式
的值为零,则x的值是 .
| x+2 |
| x-2 |
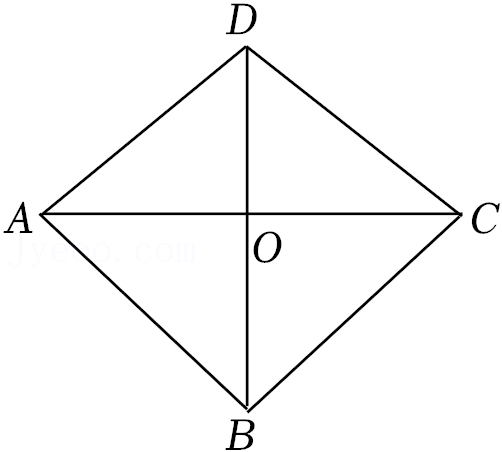
17.如图在菱形ABCD中,AC⊥BD于点O,若AD=10,AC=16,则BD= .

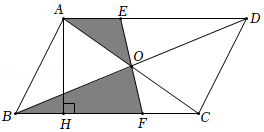
18.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,线段EF经过点O,AH⊥BC于点H.若AH=2,BC=3,则图中阴影部分的面积是 .

19.对下列多项式进行因式分解:
(1)3ab-9b.
(2)x2+4x+4.
(1)3ab-9b.
(2)x2+4x+4.
20.先化简,再求值:(1+
)÷
,其中a=4.
| 2 |
| a-1 |
| a2+2a+1 |
| a-1 |
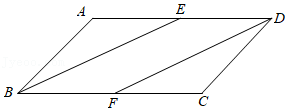
21.如图,平行四边形ABCD中,E、F分别是AD,BC的中点,求证:四边形BFDE是平行四边形.

22.解分式方程:
(1)
=
;
(2)
+1=
.
(1)
| 2 |
| x+3 |
| 1 |
| x |
(2)
| 1 |
| x-2 |
| 2x |
| x-2 |
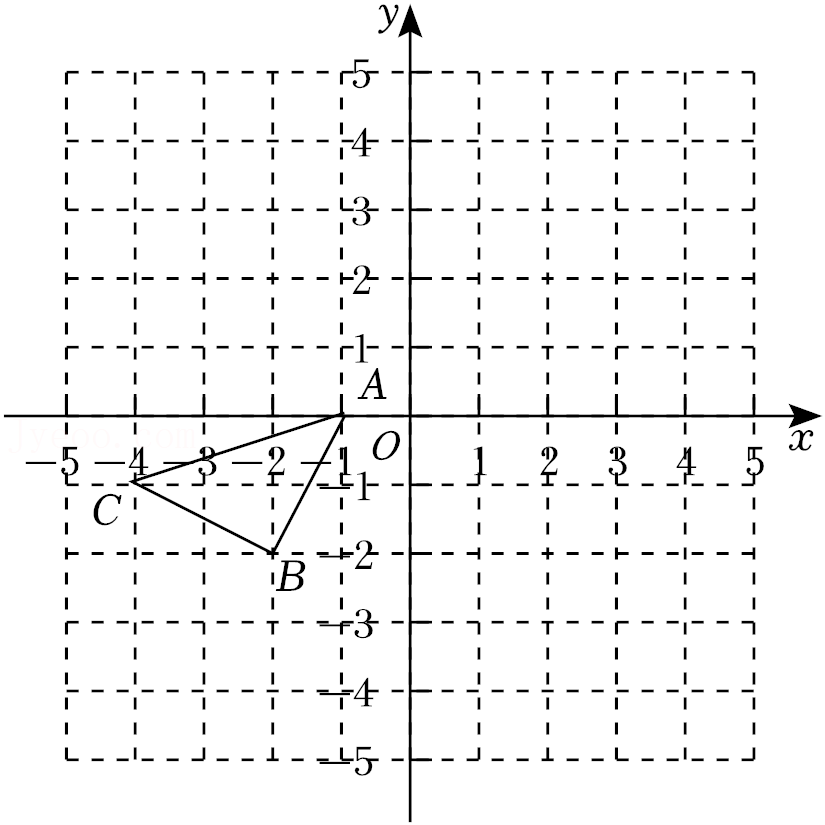
23.在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-1,0)、B(-2,-2)、C(-4,-1).(每个方格的边长均为1个单位长度)
(1)若△A1B1C1与△ABC关于原点O成中心对称(不需要画三角形),请直接写出点B1的坐标.
(2)将△ABC向上平移4个单位长度得到△A2B2C2(不需要画出),请写出点C2的坐标并求出四边形ACC2A2的面积.
(1)若△A1B1C1与△ABC关于原点O成中心对称(不需要画三角形),请直接写出点B1的坐标.
(2)将△ABC向上平移4个单位长度得到△A2B2C2(不需要画出),请写出点C2的坐标并求出四边形ACC2A2的面积.

24.2025年北京冬奥会引起了全民运动的热潮,滑雪场为了吸引儿童们从小健身锻炼,热爱雪上运动,预备开展儿童冬季雪具售卖活动,新进了数量相同的儿童雪车和滑雪板.其中,一个滑雪板的进价比雪车少5元;滑雪板和雪车分别花费6000元和6400元.请问:每个儿童雪车与滑雪板的进价各是多少元?
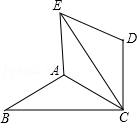
25.如图,△ABC中,∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,连接AE.
(1)求证:△ABC≌△AEC;
(2)若AB=AC,试判断四边形ACDE的形状,并说明理由.
(1)求证:△ABC≌△AEC;
(2)若AB=AC,试判断四边形ACDE的形状,并说明理由.

26.如果一个正整数能表示成两个连续偶数的平方差,那么称这个正整数为这两个连续偶数构造的“巧数”,如:4=22-02,12=42-22,20=62-42,因此4,12,20这三个数都是“巧数”.
(1)请你判断,28 (填“是”或“不是”)“巧数”;
(2)设两个连续偶数为2n和2n-2(其中n为正整数),请判断由这两个连续偶数构造的“巧数”是否为4的倍数,并证明你的结论;(提示:对“(2n)2-(2n-2)2”因式分解)
(3)请直接写出小于101的最大“巧数”.
(1)请你判断,28 (填“是”或“不是”)“巧数”;
(2)设两个连续偶数为2n和2n-2(其中n为正整数),请判断由这两个连续偶数构造的“巧数”是否为4的倍数,并证明你的结论;(提示:对“(2n)2-(2n-2)2”因式分解)
(3)请直接写出小于101的最大“巧数”.
27.如图所示,在菱形ABCD中,AB=6,∠B=60°,点E、F分别是边BC、CD上的两个动点,E点从点B向点C运动,F点从点D向点C运动,设点E、F运动的路径长分别是a和b.
(1)猜想:如图①,当a=b时,写出线段AE与线段AF的数量关系;
(2)证明:如图②,连接AC,若a+b=6,请证明△ABE≌△ACF;
(3)应用:在(2)的条件下,四边形AECF的面积是否发生变化?如果不变,请直接写出这个定值;如果变化,请直接写出该四边形面积的最大值.

(1)猜想:如图①,当a=b时,写出线段AE与线段AF的数量关系;
(2)证明:如图②,连接AC,若a+b=6,请证明△ABE≌△ACF;
(3)应用:在(2)的条件下,四边形AECF的面积是否发生变化?如果不变,请直接写出这个定值;如果变化,请直接写出该四边形面积的最大值.






