试卷题目
1.下列二次根式中最简二次根式是( )
- A. √12a
- B. √1
1 3 - C. √2
- D. √3m2n3
2.下列条件中能判定四边形ABCD是平行四边形的是( )
- A. ∠A=∠B,∠C=∠D
- B. AB=AD,CB=CD
- C. AB=CD,AD=BC
- D. AB∥CD,AD=BC
3.在三边分别为下列长度的三角形中,不是直角三角形的是( )
- A. 6,8,10
- B. 1,√2,√3
- C. 2,3,√5
- D. 4,5,7
4.下列命题:
①全等三角形的对应角相等;
②一个正数的绝对值等于本身;
③若三角形的三边长a、b、c满足a2+b2=c2,则该三角形是直角三角形.
其中逆命题是真命题的个数是( )
①全等三角形的对应角相等;
②一个正数的绝对值等于本身;
③若三角形的三边长a、b、c满足a2+b2=c2,则该三角形是直角三角形.
其中逆命题是真命题的个数是( )
- A. 0
- B. 1
- C. 2
- D. 3
5.如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
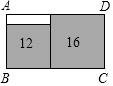

- A. 16-8√3
- B. -12+8√3
- C. 8-4√3
- D. 4-2√3
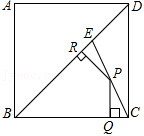
6.如图,E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )

- A. √2
2 - B.
1 2 - C. √3
2 - D.
2 3
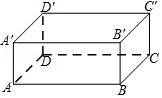
7.如图,盒内长、宽、高分别是6cm、3cm、2cm,盒内可放木棒最长的长度是( )

- A. 6cm
- B. 7cm
- C. 8cm
- D. 9cm
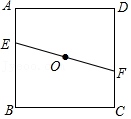
8.如图,正方形ABCD中,点O为对角线的交点,直线EF过点O分别交AB、CD于E、F两点(BE>EA),若过点O作直线与正方形的一组对边分别交于G、H两点,满足GH=EF,则这样的直线GH(不同于直线EF)的条数共有( )

- A. 1条
- B. 2条
- C. 3条
- D. 无数条
9.计算:
√(-2025)2
= .10.在平面直角坐标系中,O为原点,点M(-4,3)到原点的距离是 .
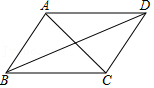
11.如图,在平行四边形ABCD中,AC=8cm,BD=14cm,则△DBC的周长比△ABC的周长多 cm.

12.已知x=
√3
+1,y=√3
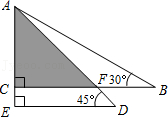
-1,则x2-y2的值为 .13.将一副三角尺如图所示叠放在一起,若AB=8cm,则阴影部分的周长是 cm.

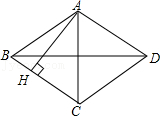
14.菱形ABCD的对角线AC=6cm,BD=8cm,AH⊥BC于H,则AH的长是 .

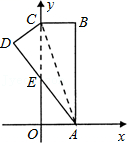
15.如图,在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点E的坐标 .

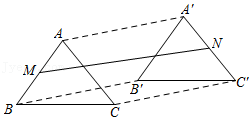
16.如图,在△ABC中,BC=6,将△ABC向任意方向平移8个单位长度得到△A'B'C',M,N分别是AB,A'C'的中点,则MN的取值范围是 .

17.计算:
(1)
(2)(
(1)
√8
+√18
-√2
-4√
;| 1 |
| 2 |
(2)(
√5
-√2
)(√5
+√2
)+(√3
-1)2.18.已知等式
成立,化简|x-6|+
√
=| 5-x |
| x-3 |
√5-x |
√x-3 |
√(x-2)2
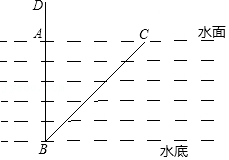
的值.19.一根直立于水中的芦节(BD)高出水面(AC)2米,一阵风吹来,芦苇的顶端D恰好到达水面的C处,且C到BD的距离AC=6米,求水的深度(AB)为多少米?

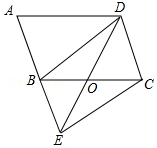
20.如图,在▱ABCD中,延长AB到点E,使BE=AB,DE交BC于点O,连接EC.
求证:四边形BECD是平行四边形.
求证:四边形BECD是平行四边形.

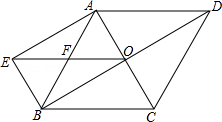
21.如图,菱形ABCD的对角线AC,BD交于点O,且BE∥AC,AE∥BD,连接EO.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若CD=6,求OE的长.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若CD=6,求OE的长.

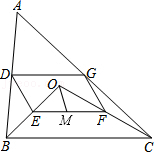
22.如图,点O是△ABC内一点,连接OA、OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连接,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若BO⊥CO,M为EF的中点,且OA=8,OM=3,求四边形DEFG的周长.
(1)求证:四边形DEFG是平行四边形;
(2)若BO⊥CO,M为EF的中点,且OA=8,OM=3,求四边形DEFG的周长.

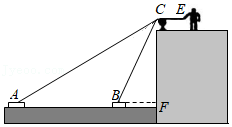
23.如图,在一条绷紧的绳索一端系着一艘小船.河岸上一男孩拽着绳子另一端向右走,绳端从C移动到E,同时小船从A移动到B,且绳长始终保持不变.回答下列问题:
(1)根据题意可知:AC BC+CE(填“>”、“<”、“=”).
(2)若CF=5米,AF=12米,AB=9米,求小男孩需向右移动的距离.(结果保留根号)
(1)根据题意可知:AC BC+CE(填“>”、“<”、“=”).
(2)若CF=5米,AF=12米,AB=9米,求小男孩需向右移动的距离.(结果保留根号)

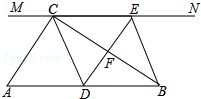
24.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)填空:
①当D是AB的中点时,四边形BECD是什么特殊四边形?答: ;
②若D是AB的中点,则当∠A的度数为 时,四边形BECD是正方形.
(1)求证:CE=AD;
(2)填空:
①当D是AB的中点时,四边形BECD是什么特殊四边形?答: ;
②若D是AB的中点,则当∠A的度数为 时,四边形BECD是正方形.

25.如图1,将矩形ABOC放置于第一象限,使其顶点O位于原点,且点B,C分别位于x轴,y轴上.若A(m,n)满足
(1)直接写出点A的坐标 ;
(2)取AC中点M,连接MO,△CMO与△NMO关于MO所在直线对称,连AN并延长交x轴于P点.求证:点P为OB的中点;
(3)如图2,在(2)的条件下,点D位于线段AC上,且CD=8.点E为平面内一动点,满足DE⊥OE,连接PE.请你直接写出线段PE长度的最大值 .

√m-10
+√20-2m
=2n-12.(1)直接写出点A的坐标 ;
(2)取AC中点M,连接MO,△CMO与△NMO关于MO所在直线对称,连AN并延长交x轴于P点.求证:点P为OB的中点;
(3)如图2,在(2)的条件下,点D位于线段AC上,且CD=8.点E为平面内一动点,满足DE⊥OE,连接PE.请你直接写出线段PE长度的最大值 .






