试卷题目
1．下列二次根式是最简二次根式的是( )
- A. √
4 3 - B. √1.5
- C. √5
- D. √40
2．2、5、m是某三角形三边的长，则
√(m-3)2
+√(m-7)2
等于( )- A. 2m-10
- B. 10-2m
- C. 10
- D. 4
3．下列说法正确的是( )
- A. 对角线互相垂直且相等的四边形是正方形
- B. 对角线相等的平行四边形是菱形
- C. 有一条对角线平分一组对角的四边形是菱形
- D. 对角线互相垂直平分的四边形是菱形
4．设6-
√10
的整数部分为a，小数部分为b，则(2a+√10
)b的值是( )- A. 6
- B. 2√10
- C. 12
- D. 9√10
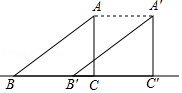
5．如图，Rt△ABC中，∠ACB=90°，AB=5，AC=3，把Rt△ABC沿直线BC向右平移3个单位长度得到△A′B ′C ′，则四边形ABC ′A′的面积是( )
- A. 15
- B. 18
- C. 20
- D. 22
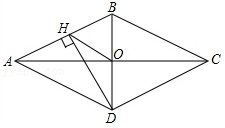
6．如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DH⊥AB于点H，连接OH，若OA=6，OH=4，则菱形ABCD的面积为( )
- A. 72
- B. 24
- C. 48
- D. 96
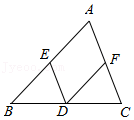
7．如图，D、E、F分别是△ABC各边中点，则以下说法错误的是( )
- A. △BDE和△DCF的面积相等
- B. 四边形AEDF是平行四边形
- C. 若AB=BC，则四边形AEDF是菱形
- D. 若∠A=90°，则四边形AEDF是矩形
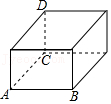
8．如图，图中有一长、宽、高分别为5cm，4cm，3cm的木箱，在它里面放入一根细木条(木条的粗细，变形忽略不计)，要求木条不能露出木箱，请你算一算，能放入的细木条的最大长度是( )
- A. √41cm
- B. √34cm
- C. 5√2cm
- D. 5√3cm
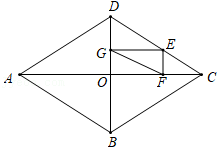
9．如图，四边形ABCD是菱形，BD=4
√2
，AD=2√6
，点E是CD边上的一动点，过点E作EF⊥OC于点F，EG⊥OD于点G，连接FG，则FG的最小值为( )- A.
5 2 - B.
12 5 - C.
4 3 √3 - D. √6
10．如图，在一张矩形纸片ABCD中，AB=4，BC=8，点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，点C落在AD上的一点H处，点D落在点G处，有以下四个结论：
①四边形CFHE是菱形；
②EC平分∠DCH；
③线段BF的取值范围为3≤BF≤4；
④当点H与点A重合时，EF=2
以上结论中，你认为正确的有( )个．
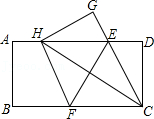
①四边形CFHE是菱形；
②EC平分∠DCH；
③线段BF的取值范围为3≤BF≤4；
④当点H与点A重合时，EF=2
√5
．以上结论中，你认为正确的有( )个．
- A. 1
- B. 2
- C. 3
- D. 4
11．计算 (
√10
+1)(√10
-1)(√10
+1)(√10
-1)的结果等于 ．12．已知a，b满足等式a2+6a+9+
√b-
=0，则a2021b2022= ．| 1 |
| 3 |
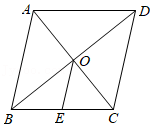
13．如图，在菱形ABCD中，对角线AC，BD相交于点O，BD=8，AC=6，OE∥AB，交BC于点E，则OE的长为 ．
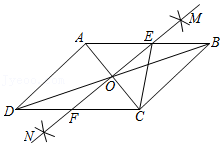
14．如图，平行四边形ABCD中，AC、BD交于O，分别以点A和点C为圆心，大于
AC的长为半径作弧，两弧相交于M、N两点，作直线MN，交AB于点E，交CD于点F，连接CE，若AD=6，△BCE的周长为14，则CD的长为 ．
| 1 |
| 2 |
15．已知x+y=-5，xy=4，则
√
+| y |
| x |
√
= ．| x |
| y |
16．如图，在四边形ABCD中，AB=BC=3，CD=
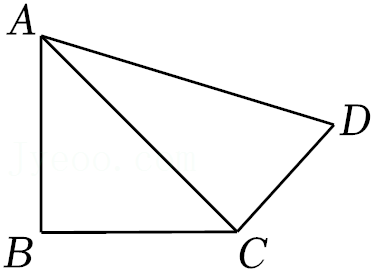
√7
，DA=5，∠B=90°，则∠BCD的度数 ．17．在矩形ABCD中，AB=2cm，将矩形ABCD沿某直线折叠，使点B与点D重合，折痕与直线AD交于点E，且DE=3cm，则矩形ABCD的面积为 cm2．
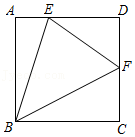
18．如图，正方形ABCD中，点E在边AD上，点F在边CD上，若∠BEF=∠EBC，AB=3AE，则下列结论：
①DF=FC；
②AE+DF=EF；
③∠BFE=∠BFC；
④∠ABE+∠CBF=45°；
⑤∠DEF+∠CBF=∠BFC；
⑥DF：DE：EF=3：4：5；
⑦BF：EF=3
其中结论正确的序号有 ．
①DF=FC；
②AE+DF=EF；
③∠BFE=∠BFC；
④∠ABE+∠CBF=45°；
⑤∠DEF+∠CBF=∠BFC；
⑥DF：DE：EF=3：4：5；
⑦BF：EF=3
√5
：5．其中结论正确的序号有 ．
19．(1)计算：(-
)-1+|1-
(2)先化简
÷(
-
)，再求值，其中x=
| 1 |
| 2 |
√2
|-√8
；(2)先化简
| x2-4 |
| x2-2x |
| x2+4x |
| x |
| 4 |
| -x |
√2
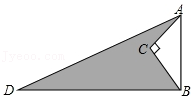
-2．20．如图，AD=13，BD=12，∠C=90°，AC=3，BC=4．求阴影部分的面积．
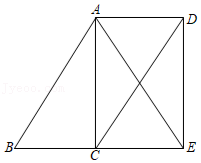
21．如图，点C是BE的中点，四边形ABCD是平行四边形．
(1)求证：四边形ACED是平行四边形；
(2)如果AB=AE，求证：四边形ACED是矩形．
(1)求证：四边形ACED是平行四边形；
(2)如果AB=AE，求证：四边形ACED是矩形．
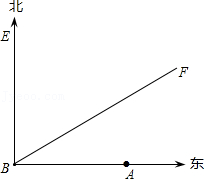
22．如图，A城气象台测得台风中心在A城正西方向320km的B处，以每小时40km的速度向北偏东60°的BF方向移动，距离台风中心200km的范围内是受台风影响的区域．
(1)A城是否受到这次台风的影响？为什么？
(2)若A城受到这次台风影响，那么A城遭受这次台风影响有多长时间？
(1)A城是否受到这次台风的影响？为什么？
(2)若A城受到这次台风影响，那么A城遭受这次台风影响有多长时间？
23．问题解决：如图1，在矩形ABCD中，点E，F分别在AB，BC边上，DE=AF，DE⊥AF于点G．
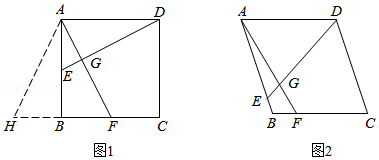
(1)求证：四边形ABCD是正方形；
(2)延长CB到点H，使得BH=AE，判断△AHF的形状，并说明理由．
(3)类比迁移：如图2，在菱形ABCD中，点E，F分别在AB，BC边上，DE与AF相交于点G，DE=AF，∠AED=60°，AE=6，BF=2，求DE的长．
(1)求证：四边形ABCD是正方形；
(2)延长CB到点H，使得BH=AE，判断△AHF的形状，并说明理由．
(3)类比迁移：如图2，在菱形ABCD中，点E，F分别在AB，BC边上，DE与AF相交于点G，DE=AF，∠AED=60°，AE=6，BF=2，求DE的长．
24．如图，在长方形ABCD中，AB=4cm，BE=5cm，点E是AD边上的一点，AE、DE分别长acm、bcm，满足(a-3)2+|2a+b-9|=0．动点P从B点出发，以2cm/s的速度沿B→C→D运动，最终到达点D．设运动时间为ts．
(1)a= cm，b= cm；
(2)t为何值时，EP把四边形BCDE的周长平分？
(3)另有一点Q从点E出发，按照E→D→C的路径运动，且速度为1cm/s，若P、Q两点同时出发，当其中一点到达终点时，另一点随之停止运动．求t为何值时，△BPQ的面积等于6cm2．
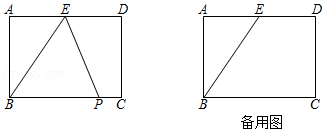
(1)a= cm，b= cm；
(2)t为何值时，EP把四边形BCDE的周长平分？
(3)另有一点Q从点E出发，按照E→D→C的路径运动，且速度为1cm/s，若P、Q两点同时出发，当其中一点到达终点时，另一点随之停止运动．求t为何值时，△BPQ的面积等于6cm2．
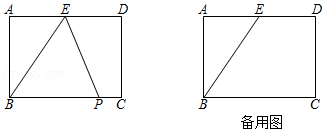
25．将正方形ABCD放置在平面直角坐标系中，B与原点重合，点A的坐标为(0，a)，点E的坐标为(b，0)，并且实数a，b使式子b=
(1)直接写出点D、E的坐标：D ，E ．
(2)∠AEF=90°，且EF交正方形外角的平分线CF于点F．
①如图①，求证AE=EF；
②如图②，连接AF交DC于点G，作GM∥AD交AE于点M，作EN∥AB交AF于点N，连接MN，求四边形MNGE的面积．
(3)如图③，连接正方形ABCD的对角线AC，若点P在AC上，点Q在CD上，且AP=CQ，请直接写出(BP+BQ)2的最小值 ．
√12-2a
+√a-6
+3成立．(1)直接写出点D、E的坐标：D ，E ．
(2)∠AEF=90°，且EF交正方形外角的平分线CF于点F．
①如图①，求证AE=EF；
②如图②，连接AF交DC于点G，作GM∥AD交AE于点M，作EN∥AB交AF于点N，连接MN，求四边形MNGE的面积．
(3)如图③，连接正方形ABCD的对角线AC，若点P在AC上，点Q在CD上，且AP=CQ，请直接写出(BP+BQ)2的最小值 ．
