试卷题目
1.式子
√x+1
有意义,则x的取值范围是( )- A. x≥-1
- B. x≤-1
- C. x≥1
- D. x≤1
2.下列计算正确的是( )
- A. √2+√3=√5
- B. √4-√2=√2
- C. √8=4√2
- D. √2×√3=√6
3.一个四边形的三个相邻内角度数依次如下,那么其中是平行四边形的是( )
- A. 88°,108°,88°
- B. 88°,104°,108°
- C. 88°,92°,92°
- D. 88°,92°,88°
4.a、b、c为△ABC三边,不是直角三角形的是( )
- A. a2=c2-b2
- B. a=,b=1,c=
5 4 3 4 - C. ∠A:∠B:∠C=3:4:5
- D. a=8k,b=17k,c=15k
5.下列关于菱形、矩形的说法正确的是( )
- A. 菱形的对角线相等且互相平分
- B. 矩形的对角线相等且互相平分
- C. 对角线互相垂直的四边形是菱形
- D. 对角线相等的四边形是矩形
6.若
√(1-m)2
=m-1,则m的取值范围是( )- A. 一切实数
- B. m≤1
- C. m≥1
- D. m=1
7.已知
√18-m
是整数,求自然数m的所有可能值的个数为( )- A. 3个
- B. 4个
- C. 5个
- D. 无数个
8.点O是矩形ABCD的对角线AC的中点,E是BC边的中点,AD=8,OE=3,则线段OD的长为( )
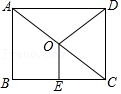

- A. 5
- B. 6
- C. 8
- D. 10
9.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
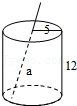

- A. 12≤a≤13
- B. 12≤a≤15
- C. 5≤a≤12
- D. 5≤a≤13
10.如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( )
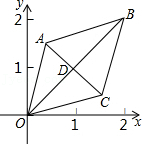

- A. (1,-1)
- B. (-1,-1)
- C. (√2,0)
- D. (0,-√2)
11.在实数范围内分解因式a2-6= .
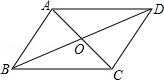
12.如图,已知▱ABCD的对角线AC,BD交于点O,且AC=8,BD=10,AB=5,则△OCD的周长为 .

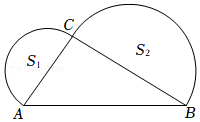
13.如图,Rt△ABC中,∠ACB=90°,以AC、BC为直径作半圆S1和S2,且S1+S2=2π,则AB的长为 .

14.已知一个直角三角形的两条边的长分别为3和5,则第三条边的长为
.
.
15.对于任意的正数m,n定义运算*为:m*n=
,计算(3*2)+(8*12)的结果为 .
| { |
|
16.如图,在菱形ABCD中,∠ABC=60°,BC=4
√3
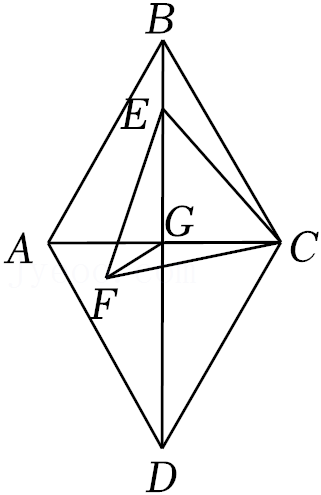
,对角线AC、BD相交于点G,E是对角线BD上的一个动点,连接CE,将线段CE绕点C逆时针旋转60°得到CF,连接EF,FG,在点E运动过程中,线段FG长度的最小值是 .
17.计算:
(1)
(2)(2
(1)
√18
-√32
+√2
(2)(2
√48
-3√27
)÷√6
.18.已知x=
(1)x2+2xy+y2;
(2)x2-y2.
√3
+1,y=√3
-1,求下列各式的值:(1)x2+2xy+y2;
(2)x2-y2.
19.我国古代数学著作《九章算术》中有这样一个问题:“今有池方一丈,葭(jiā)生其中央,出水一尺,引葭赴岸,适与岸齐,问水深几何?”(注:丈,尺是长度单位,1丈=10尺,1尺=
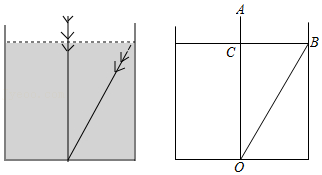
米)这段话翻译成现代汉语,即为:如图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.则水池里水的深度是多少米?请你用所学知识解答这个问题.
| 1 |
| 3 |

20.如图,在4×3正方形网格中,每个小正方形的边长都是1
(1)分别求出线段AB、CD的长度;
(2)在图中画线段EF、使得EF的长为
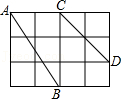
(1)分别求出线段AB、CD的长度;
(2)在图中画线段EF、使得EF的长为
√5
,以AB、CD、EF三条线段能否构成直角三角形,并说明理由.
21.如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、作CE∥BD,DE∥AC,CE和DE交于点E
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=10时,求CE和AE的长.
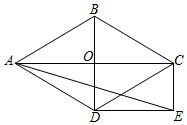
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=10时,求CE和AE的长.

22.两张宽度均为4的矩形纸片按如图所示方式放置.
(1)猜想四边形ABCD的形状,并说明理由;
(2)若S四边形ABCD=16
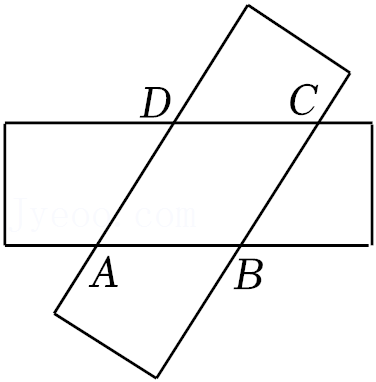
(1)猜想四边形ABCD的形状,并说明理由;
(2)若S四边形ABCD=16
√2
,求∠BAD的度数.
23.如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,∠ACB=∠ECD=90°,△ACB的顶点A在△ECD的斜边上.
(1)直接写出线段AE和BD之间的关系;
(2)猜想线段AE、AD、AC之间的数量关系,并证明你的猜想;
(3)若AE=
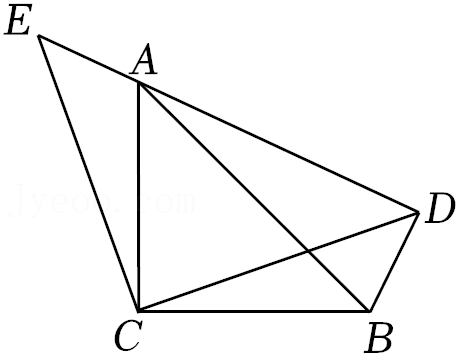
(1)直接写出线段AE和BD之间的关系;
(2)猜想线段AE、AD、AC之间的数量关系,并证明你的猜想;
(3)若AE=
√2
,CE=1+√3
,直接写出线段AC的长.
24.在平面直角坐标系中,矩形OABC的顶点O、A、C的坐标分别为O(0,0),A(-x,0),C(0,y),且x、y满足y=
(1)矩形的顶点B的坐标是 ;
(2)若D是AB中点,沿DO折叠矩形OABC,使A点落在点E处,折痕为DO,连BE并延长BE交y轴于Q点.求证:四边形DBQO是平行四边形;
(3)在(2)的条件下,求△OEQ的面积.
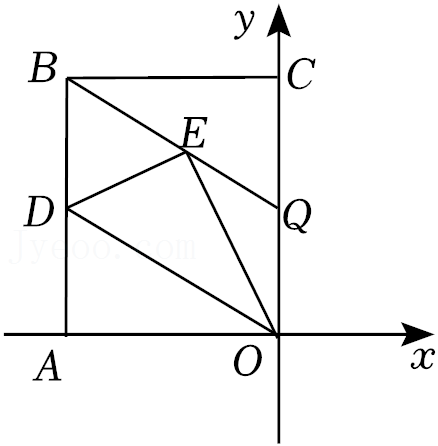
√x-4
+√4-x
+6.(1)矩形的顶点B的坐标是 ;
(2)若D是AB中点,沿DO折叠矩形OABC,使A点落在点E处,折痕为DO,连BE并延长BE交y轴于Q点.求证:四边形DBQO是平行四边形;
(3)在(2)的条件下,求△OEQ的面积.






