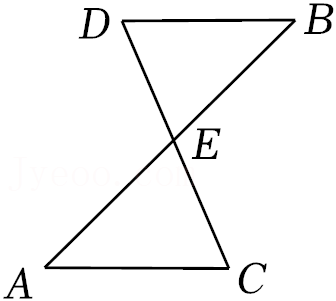试卷题目
1.在下列实数中,无理数是( )
- A.
5 3 - B. 3√-27
- C. √0.01
- D. 2π
2.下列说法正确的是( )
- A. 1的立方根是±1
- B. √4=±2
- C. √81的平方根是±3
- D. 0没有平方根
3.下列各式计算结果正确的是( )
- A. x3+x3=x6
- B. b(b+b3)=b4
- C. 4a3•2a2=8a5
- D. 5a2-3a2=2
4.下列式子从左到右的变形中,属于因式分解的是( )
- A. (x+1)(x-1)=x2-1
- B. a2-b2=(a+b)(a-b)
- C. x2-2x+1=x(x-2)+1
- D. mx+my+nx+ny=m(x+y)+n(x+y)
5.与数轴上的点一一对应的数是( )
- A. 分数
- B. 有理数
- C. 无理数
- D. 实数
6.若x+m与x+3的乘积中不含x的一次项,则m的值为( )
- A. 0
- B. 1
- C. 3
- D. -3
7.下列多项式相乘,结果为a2+6a-16的是( )
- A. (a-2)(a-8)
- B. (a+2)(a-8)
- C. (a-2)(a+8)
- D. (a+2)(a+8)
8.下列命题不正确的是( )
- A. 直角三角形的两个锐角互补
- B. 两点确定一条直线
- C. 两点之间线段最短
- D. 三角形内角和为180°
9.如图,黑色部分长方形的面积为( )
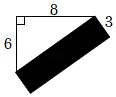

- A. 24
- B. 30
- C. 40
- D. 48
10.估算
√24
+3的值是在( )之间.- A. 5和6
- B. 6和7
- C. 7和8
- D. 8和9
11.下列说法中,正确的个数是( )
①实数包括有理数、无理数和零;
②一个锐角加上一个钝角等于一平角是真命题;
③幂的乘方,底数不变,指数相加;
④平方根与立方根都等于它本身的数为1和0.
①实数包括有理数、无理数和零;
②一个锐角加上一个钝角等于一平角是真命题;
③幂的乘方,底数不变,指数相加;
④平方根与立方根都等于它本身的数为1和0.
- A. 3个
- B. 2个
- C. 1个
- D. 0个
12.如图,有一个长、宽、高分别为2m、3m、1m的长方体,现一只蚂蚁沿长方体表面从A点爬到B点,那么最短的路径是( )


- A. 2√5m
- B. √3m
- C. 3√2m
- D. 2m
13.若
3√x
=3,则x= .14.若xm=5,xn=4.则xm-n= .
15.计算:x3•(2x3)2÷(x4)2= .
16.如果
√2a-6
有意义,那么a的取值范围是 .17.分解因式:8a(x-a)+4b(a-x)-6c(x-a)= .(直接写出结果)
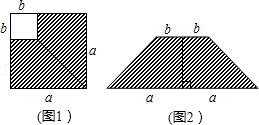
18.如图1,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下部分拼成一个梯形(如图2),利用这两幅图形面积,可以验证的乘法公式是 .

19.计算:
(1)
(2)(16x3-8x2+4x)÷(-2x).
(1)
√52
-3√8
+√4
;(2)(16x3-8x2+4x)÷(-2x).
20.因式分解
(1)a3-4a2+4a;
(2)(x-1)(x-3)-8.
(1)a3-4a2+4a;
(2)(x-1)(x-3)-8.
21.先化简,再求值:(3x-y)2+(3x+y)(3x-y),其中x=1,y=-2.
22.已知实数a、b、c满足2|a-2020|=2c-c2-1,求ca的值.
23.我市《道路交通管理条例》规定:小汽车在城市街道上的行驶速度不得超过60km/h.如图,一辆小汽车在一条城市街道上沿直道行驶,某一时刻刚好行驶到车速检测点A正前方30m的C处,2秒后又行驶到与车速检测点A相距50m的B处.请问这辆小汽车超速了吗?若超速,请求出超速了多少?


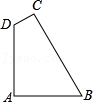
24.如图,在四边形ABCD中,AB=AD,∠DAB=∠BCD=90°,设P=BC+CD,四边形ABCD的面积为S.
(1)试探究S与P之间的关系,并说明理由;
(2)若四边形ABCD的面积为12,求BC+CD的值.
(1)试探究S与P之间的关系,并说明理由;
(2)若四边形ABCD的面积为12,求BC+CD的值.

25.(1)已知2a-b的平方根为±2,3a+b-2的算术平方根为3,求10a+3b的平方根.
(2)如图:已知线段AB与CD相交于点E,且AC∥BD,AE=EB,求证:AC=DB.
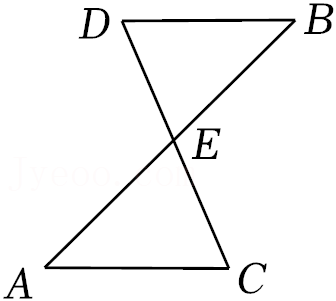
(2)如图:已知线段AB与CD相交于点E,且AC∥BD,AE=EB,求证:AC=DB.