试卷题目
1.下列二次根式中,是最简二次根式的是( )
- A. √4
- B. √12
- C. √
1 2 - D. √7
2.下列计算结果正确的是( )
- A. √2+√3=√5
- B. 2√2-√2=2
- C. √2×√3=√6
- D. =3√2√3√6
3.下列各式成立的是( )
- A. √22=±2
- B. √(-2)2=2
- C. √(-2)2=-2
- D. √(-2)2=±2
4.在Rt△ABC中,∠C=90°,CD是AB边上的中线,下列结论正确的是( )
- A. CD⊥AB
- B. CD=BC
- C. BD=CD
- D. ∠ACD=∠BCD
5.下列各组数,可以作为直角三角形的三边长的是( )
- A. 2,3,4
- B. 3,4,5
- C. 4,5,6
- D. 5,6,7
6.如图,D,E分别是△ABC的边AB,AC的中点,下列结论错误的是( )
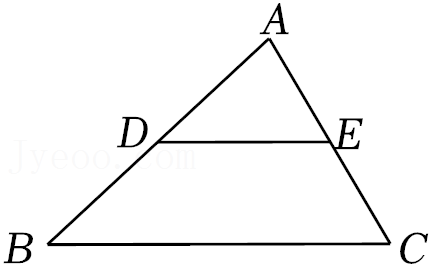

- A. DE∥BC
- B. DE=BC
1 2 - C. △ADE的周长是△ABC周长的一半
- D. S△ADE=S△ABC
1 2
7.下列命题中正确的是( )
- A. 有一组邻边相等的四边形是菱形
- B. 有一个角是直角的平行四边形是矩形
- C. 对角线垂直的平行四边形是正方形
- D. 一组对边平行的四边形是平行四边形
8.在菱形ABCD中,点O为对角线AC的中点,点E为AB边上一动点(点E不与点A,B重合),连接EO并延长交CD于点F,连接AF,CE,若四边形AECF一定不是矩形,则∠BAD应满足的条件是( )
- A. 0°<∠BAD≤90°
- B. 45°<∠BAD≤135°
- C. 90°<∠BAD<180°
- D. 0°<∠BAD<180°
9.若二次根式
√x-4
在实数范围内有意义,则x的取值范围是 .10.计算:
√8
= .11.已知一个平行四边形两个内角的度数比为1:3,则其中较小的内角为 .
12.计算:
√12
-√3
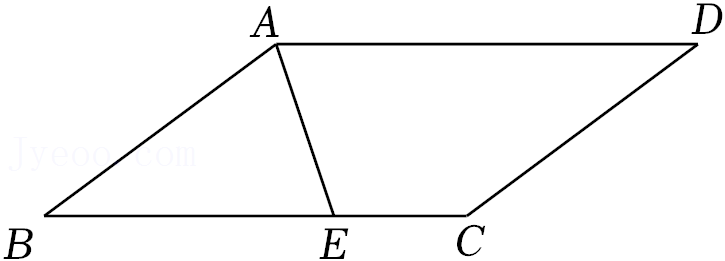
= .13.如图,在▱ABCD中,AD=10,AB=7,AE平分∠BAD交BC于点E,则EC的长为 .

14.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?”译文是:“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺(实际含义是:绳索比木柱长3尺).牵着绳索(绳索头与地面接触)退行,在距木柱根部8尺处时绳索用尽.问绳索长是多少?”设绳索长x尺,根据题意列方程为 .
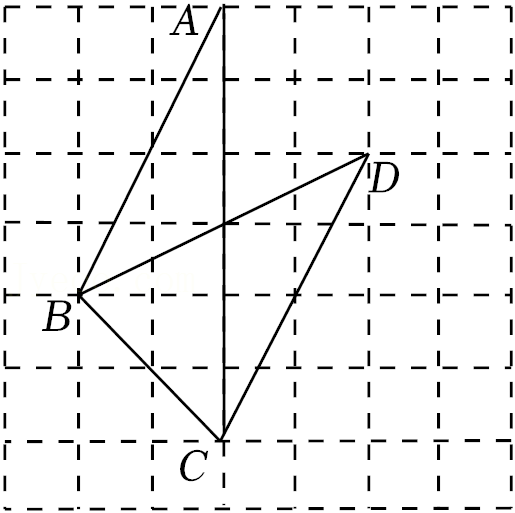
15.如图所示的网格是正方形网格,点A,B,C,D是网格线交点,则△ABC的面积与△BCD的面积的大小关系为:S△ABC S△BCD(填“>”,“=”或“<”).

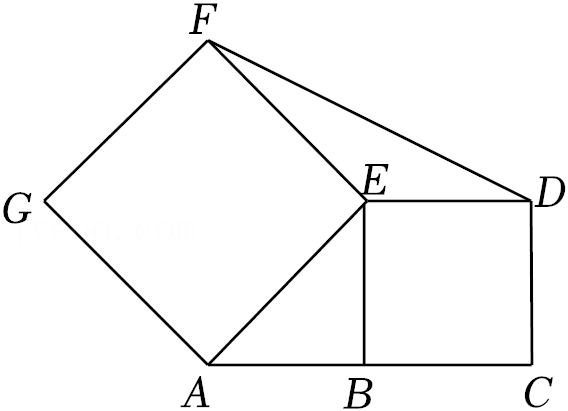
16.如图,点C为线段AB延长线上一点,正方形AEFG和正方形BCDE的面积分别为8和4,则△EDF的面积为 .

17.计算:
+
√12
×√3 |
| 2 |
√24
÷√6
18.计算(
√5
+√2
)(√5
-√2
)19.计算:|2-
)-1
√3
|-(π-√5
)0+√75
-(| 1 |
| 3 |
20.如图,在平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,连接AF,CE.求证:四边形AECF是平行四边形.


21.如图,在四边形ABCD中,∠A=90°,AB=AD=
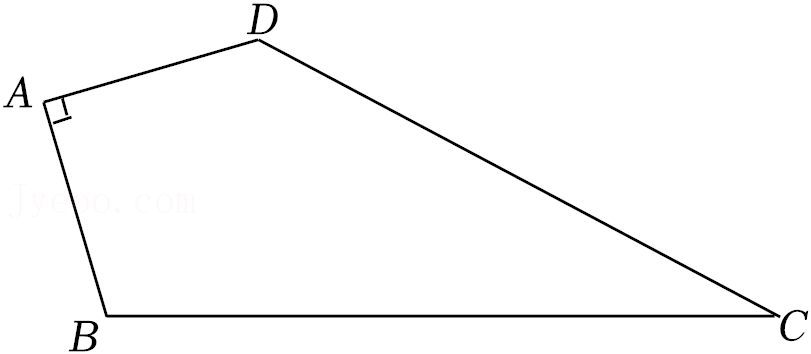
√2
,BC=2√5
,CD=4.求∠ADC的度数.
22.观察下列各式:
n=1时,有式①:
n=2时,有式②:
;
(1)类比上述式①、式②,将下列等式补充完整:
(2)请用含n(n为正整数)的等式表示以上各式的运算规律: .
n=1时,有式①:
√1+
=| 1 |
| 3 |
| 2 |
| 3 |
√3
;n=2时,有式②:
√2+
=| 1 |
| 4 |
| 3 |
| 4 |
√4
=| 3 |
| 2 |
(1)类比上述式①、式②,将下列等式补充完整:
√3+
= ;| 1 |
| 5 |
√( )+
=| 1 |
| ( ) |
| 5 |
| 6 |
√6
;(2)请用含n(n为正整数)的等式表示以上各式的运算规律: .
23.如图,菱形ABCD对角线AC,BD相交于点O,点E是AD的中点,过点A作对角线AC的垂线,与OE的延长线交于点F,连接FD.
(1)求证:四边形AODF是矩形;
(2)若AD=10,∠ABC=60°,求OF和OA的长.
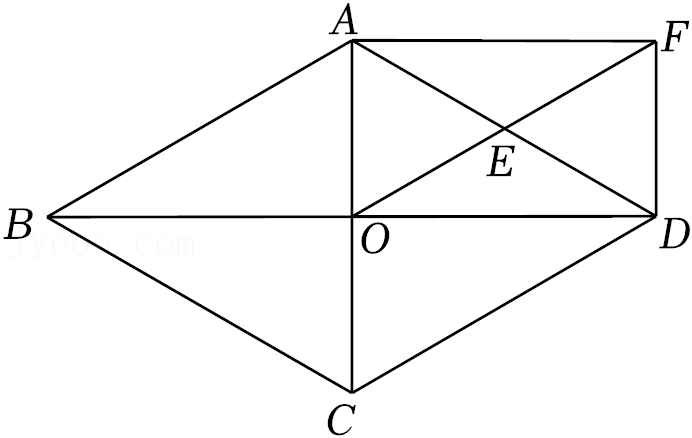
(1)求证:四边形AODF是矩形;
(2)若AD=10,∠ABC=60°,求OF和OA的长.

24.如图,在四边形ABCD中,AD=CD,BD⊥AC于点O,点E是DB延长线上一点,OE=OD,BF⊥AE于点F.
(1)求证:四边形AECD是菱形;
(2)若AB平分∠EAC,OB=3,BE=5,求EF和AD的长.
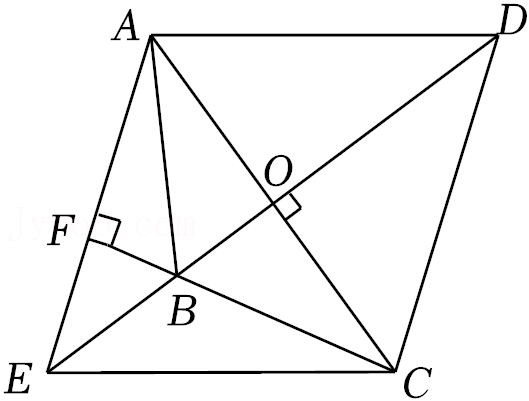
(1)求证:四边形AECD是菱形;
(2)若AB平分∠EAC,OB=3,BE=5,求EF和AD的长.

25.如图,在数轴上标出表示1的点A,和表示5的点B,过点O作直线l垂直于OA,以点A为圆心,以AB为半径在数轴的上方作弧,弧与直线l交于点C,以点O为圆心,以OC为半径作弧,弧与数轴正半轴的交点D即为表示
(1)依题意,用直尺和圆规完成作图(保留作图痕迹);
(2)根据作图,利用勾股定理,可以发现,如果在直角三角形中,一边长为
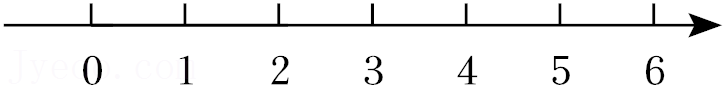
√15
的点.(1)依题意,用直尺和圆规完成作图(保留作图痕迹);
(2)根据作图,利用勾股定理,可以发现,如果在直角三角形中,一边长为
√15
,其他两边均为正整数,那么长为√15
的边是直角三角形的 (填“直角边”或“斜边”),直角三角形另两条边长分别为 、 .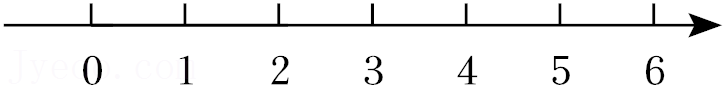
26.在平面直角坐标系xOy中,点A(-4,0),点B位于y轴正半轴,AB=4
(1)求点B,C的坐标;
(2)垂直于y轴的直线l与线段AB,BC分别交于点D,E,过点D作DF⊥AC,垂足为F,过点E作EG⊥AC,垂足为G,横、纵坐标都是整数的点叫做整点,记四边形DFGE围成的区域(不含边界)为W.若点D的纵坐标为yD,当区域W内整点个数达到最多时,直接写出yD的取值范围.
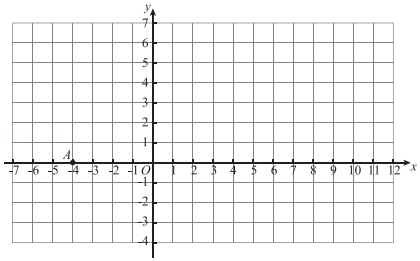
√2
,点C位于x轴正半轴,∠OCB=30°.(1)求点B,C的坐标;
(2)垂直于y轴的直线l与线段AB,BC分别交于点D,E,过点D作DF⊥AC,垂足为F,过点E作EG⊥AC,垂足为G,横、纵坐标都是整数的点叫做整点,记四边形DFGE围成的区域(不含边界)为W.若点D的纵坐标为yD,当区域W内整点个数达到最多时,直接写出yD的取值范围.

27.已知四边形ABCD是正方形,点E为射线AC上一动点(点E不与A,C重合),连接DE,过点E作EF⊥DE,交射线BC于点F,过点D,F分别作DE,EF的垂线,两垂线交于点G,连接CG.
(1)如图,当点E在对角线AC上时,依题意补全图形,并证明:四边形DEFG是正方形;
(2)在(1)的条件下,猜想:CE,CG和AC的数量关系,并加以证明;
(3)当点E在对角线AC的延长线上时,直接用等式表示CE,CG和AC的数量关系.
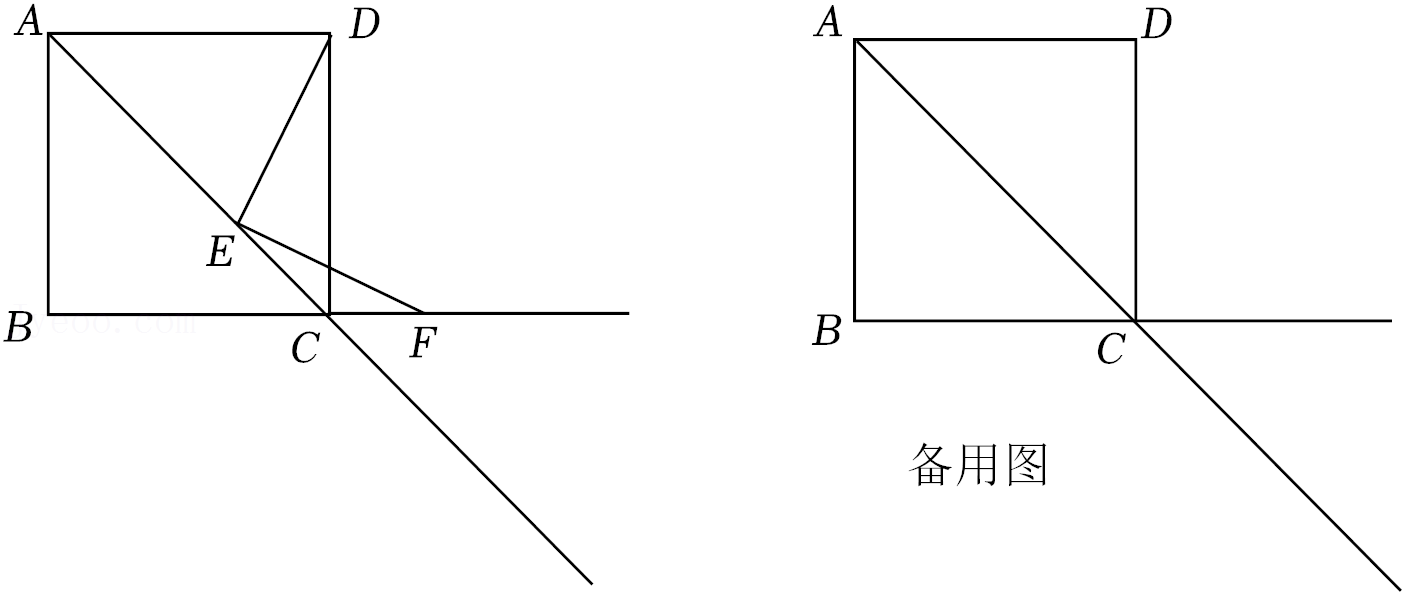
(1)如图,当点E在对角线AC上时,依题意补全图形,并证明:四边形DEFG是正方形;
(2)在(1)的条件下,猜想:CE,CG和AC的数量关系,并加以证明;
(3)当点E在对角线AC的延长线上时,直接用等式表示CE,CG和AC的数量关系.

28.对于平面直角坐标系xOy中的线段AB和图形M,给出如下的定义:若图形M是以AB为对角线的平行四边形,则称图形M是线段AB的“关联平行四边形”.
点A(8,a),点B(2,b),
(1)当a=8,b=-2时,若四边形AOBC是线段AB的“关联平行四边形”,则点C的坐标是 ;
(2)若四边形AOBC是线段AB的“关联平行四边形”,求对角线OC的最小值;
(3)若线段AB的“关联平行四边形”AOBC是正方形,直接写出点C的坐标.

点A(8,a),点B(2,b),
(1)当a=8,b=-2时,若四边形AOBC是线段AB的“关联平行四边形”,则点C的坐标是 ;
(2)若四边形AOBC是线段AB的“关联平行四边形”,求对角线OC的最小值;
(3)若线段AB的“关联平行四边形”AOBC是正方形,直接写出点C的坐标.






