试卷题目
1.若二次根式
√x-1
有意义,则x的取值范围是( )- A. x≥1
- B. x≤1
- C. x>1
- D. x≠1
2.下列各组数中不能作为直角三角形的三边长的是( )
- A. 1.5,2,2
- B. 7,24,25
- C. 6,8,10
- D. 9,12,15
3.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

- A. 当AB=BC时,它是菱形
- B. 当AC⊥BD时,它是菱形
- C. 当∠ABC=90°时,它是矩形
- D. 当AC=BD时,它是正方形
4.一次函数y=-2x+3的图象所经过的象限是( )
- A. 一、二、三
- B. 二、三、四
- C. 一、三、四
- D. 一、二、四
5.北京今年6月某日部分区县的高气温如表:则这10个区县该日最高气温的众数和中位数分别是( )
| 区县 | 大兴 | 通州 | 平谷 | 顺义 | 怀柔 | 门头沟 | 延庆 | 昌平 | 密云 | 房山 |
| 最高气温 | 32 | 32 | 30 | 32 | 30 | 32 | 29 | 32 | 30 | 32 |
- A. 32,32
- B. 32,30
- C. 30,32
- D. 32,31
6.如图,在平行四边形ABCD中,AD=2AB,F是BC的中点,作AE⊥CD于点E,连接EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF=S△AEF;④∠BFE=3∠CEF.其中一定成立的个数是( )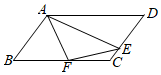

- A. 1个
- B. 2个
- C. 3个
- D. 4个
7.
√27
-√3
= .8.若一直角三角形两直角边长分别为6和8,则斜边长为 .
9.如图,在正方形ABCD的外侧,作等边△DCE,则∠AEC的度数是 .

10.如图是一次函数y=ax+b的图象,则关于x的不等式ax+b<0的解集为 .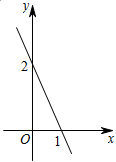
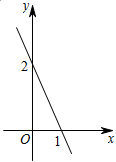
11.甲、乙两地9月上旬的日平均气温如图所示,则甲、乙两地这10天日平均气温的方差大小关系为s甲2 s乙2(填>或<).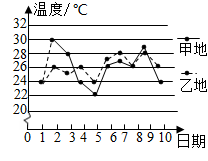

12.在平面直角坐标系中,直线y=
x-8与x轴,y轴分别交于点A,B.M是y轴上一点.若将△ABM沿AM折叠,点B恰好落在坐标轴上,则点M的坐标为 .
| 4 |
| 3 |
13.计算:
(1)
(2)(
(1)
√12
+√3
-√27
;(2)(
√7
-2)2.14.如图:在▱ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=25°,求∠C、∠B的度数.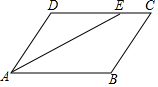

15.如图,CD是△ABC的高,若AC=3,BC=4,AB=5.
(1)求证:∠BCA=90°;
(2)求CD的长.
(1)求证:∠BCA=90°;
(2)求CD的长.

16.声音在空气中的传播速度y(m/s)随气温x(℃)的变化而变化.如表给出了一组不同气温下声音传播的速度:
(1)求y与x的关系式;
(2)当x的值为35时,求对应的y的值.
| x(℃) | 0 | 5 | 10 | 15 | 20 | 25 |
| y(m/s) | 331 | 334 | 337 | 340 | 343 | 346 |
(1)求y与x的关系式;
(2)当x的值为35时,求对应的y的值.
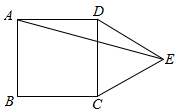
17.如图四边形ABCD是平行四边形,请仅用无刻度的直尺按要求作图:
(1)在图1中作一条线段,将▱ABCD的面积平均分成两份;
(2)在图2中过点E作一条直线,将▱ABCD的面积平均分成两份.

(1)在图1中作一条线段,将▱ABCD的面积平均分成两份;
(2)在图2中过点E作一条直线,将▱ABCD的面积平均分成两份.

18.某校招聘一名数学老师,对应聘者分别进行了教学能力、科研能力和组织能力三项测试,其中甲、乙两名应聘者的成绩如右表:(单位:分)
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将被录用?
(2)根据实际需要,学校将教学、科研和组织能力三项测试得分按 5:3:2 的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
| 教学能力 | 科研能力 | 组织能力 | |
| 甲 | 81 | 85 | 86 |
| 乙 | 92 | 80 | 74 |
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将被录用?
(2)根据实际需要,学校将教学、科研和组织能力三项测试得分按 5:3:2 的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
19.观察下列各式及其验证过程:
验证:2
验证:2
验证:3
验证:3
(1)按照上述两个等式及其验证过程的基本思路,猜想4
(2)针对上述各式反映的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并给出证明.
验证:2
√
=| 2 |
| 3 |
√2+
;| 2 |
| 3 |
验证:2
√
=| 2 |
| 3 |
√
=| 23 |
| 3 |
√
=| (23-2)+2 |
| 22-1 |
√
=| 2(22-1)+2 |
| 22-1 |
√2+
;| 2 |
| 3 |
验证:3
√
=| 3 |
| 8 |
√3+
;| 3 |
| 8 |
验证:3
√
=| 3 |
| 8 |
√
=| 33 |
| 8 |
√
=| (33-3)+3 |
| 32-1 |
√
=| 3(32-1)+3 |
| 32-1 |
√3+
.| 3 |
| 8 |
(1)按照上述两个等式及其验证过程的基本思路,猜想4
√
的变形结果并进行验证;| 4 |
| 15 |
(2)针对上述各式反映的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并给出证明.
20.如图,在矩形ABCD中,AB=8cm,BC=16cm,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为t s.
(1)当t为何值时,四边形ABQP是矩形;
(2)当t为何值时,四边形AQCP是菱形;
(3)分别求出(2)中菱形AQCP的周长和面积.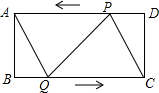
(1)当t为何值时,四边形ABQP是矩形;
(2)当t为何值时,四边形AQCP是菱形;
(3)分别求出(2)中菱形AQCP的周长和面积.

21.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展,现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°.AC=b,BC=a,AB=c,请你利用这个图形解决下列问题:
(1)试说明:a2+b2=c2;
(2)如果大正方形的面积是13,小正方形的面积是3,求(a+b)2的值.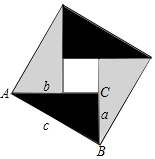
(1)试说明:a2+b2=c2;
(2)如果大正方形的面积是13,小正方形的面积是3,求(a+b)2的值.

22.在一条笔直的道路上依次有甲、乙、丙三地,小刚与小亮在这条道路上练习跑步,小刚从甲地匀速跑步到丙地,同时小亮从乙地匀速跑步到甲地,在甲地休息2分钟后,以另一速度匀速跑步到丙地,小刚、小亮距甲地的路程y(米)与小刚跑步的时间x(分)之间的函数关系如图所示.
(1)a的值为 ,乙地与丙地相距 米.
(2)求小亮从甲地到丙地y与x之间的函数关系式.
(3)直接写出小刚到达丙地前两人距乙地的路程相等时x的值.
(1)a的值为 ,乙地与丙地相距 米.
(2)求小亮从甲地到丙地y与x之间的函数关系式.
(3)直接写出小刚到达丙地前两人距乙地的路程相等时x的值.

23.定义:我们把两条对角线互相垂直的四边形称为“垂美四边形”.
(1)特例感知:如图1,四边形ABCD是“垂美四边形”,如果OA=OD=
OB,OB=2,∠OBC=60°,则AD2+BC2= ,AB2+CD2= .
(2)猜想论证:如图1,如果四边形ABCD是“垂美四边形”,猜想它的两组对边AB,CD与BC,AD之间的数量关系并给予证明.
(3)拓展应用:如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,∠BAC=60°,求GE长.
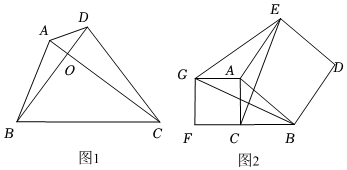
(1)特例感知:如图1,四边形ABCD是“垂美四边形”,如果OA=OD=
| 1 |
| 3 |
(2)猜想论证:如图1,如果四边形ABCD是“垂美四边形”,猜想它的两组对边AB,CD与BC,AD之间的数量关系并给予证明.
(3)拓展应用:如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,∠BAC=60°,求GE长.






