试卷题目
1.在以下绿色食品、低碳、节能、节水四个标志中,是轴对称图形的是( )
- A.

- B.

- C.

- D.

2.从五边形的其中一个顶点出发,一共可以引出的对角线条数有( )
- A. 2条
- B. 3条
- C. 5条
- D. 6条
3.下列计算正确的是( )
- A. (a3)2=a5
- B. a6÷a3=a3
- C. (-2a)3=-2a3
- D. 2a2•a3=2a6
4.在显微镜下测得一个病毒的直径为0.00000000205米,该数据用科学记数法表示为( )
- A. 0.205×10-8米
- B. 2.05×109米
- C. 20.5×10-10米
- D. 2.05×10-9米
5.等腰△ABC中,AB=AC,若∠A=70°,则∠B的度数是( )
- A. 40°
- B. 55°
- C. 65°
- D. 60°
6.下列多项式不能用公式法分解因式的是( )
- A. -x2+y2
- B. -y2-2xy-x2
- C. x2-2xy+y2
- D. x2+y2
7.若分式
□
的运算结果为x(x≠0),则在“口”中添加的运算符号为( )
| x2 |
| x+1 |
| x |
| x+1 |
- A. +
- B. -
- C. +或÷
- D. -或×
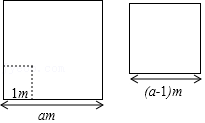
8.如图,“丰收1号”小麦的试验田是边长为am(a>1)的正方形去掉一个边长为1m的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a-1)m的正方形,两块试验田的小麦都收获了500kg.则对于这两种水稻的单位面积产量说法正确的是( )

- A. “丰收1号”水稻单位面积产量高
- B. “丰收2号”水稻单位面积产量高
- C. 两种水稻单位面积产量一样多
- D. 无法判断
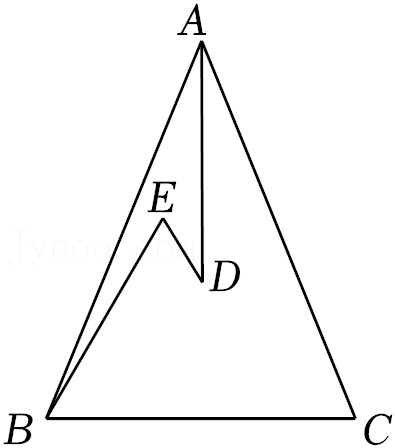
9.如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=10cm,DE=4cm,则BC的长为( )

- A. 7cm
- B. 12cm
- C. 14cm
- D. 16cm
10.如图,将等边△ABC折叠,使得点C恰好落在边AB上的点D处,折痕为EF,O为折痕EF上一动点,若AD=2,AB=6,则△OBD周长的最小值是( )












