试卷题目
1.二次根式
√x-1
中,x的取值范围是( )- A. x≥1
- B. x>1
- C. x≤1
- D. x<1
2.下列各组数是三角形的三边,不能组成直角三角形的一组数是( )
- A. 1,1,√2
- B. 3,4,5
- C. 5,12,13
- D. √3,√4,√5
3.下列图形:平行四边形、矩形、菱形、等腰梯形、正方形中是轴对称图形的有( )个.
- A. 1
- B. 2
- C. 3
- D. 4
4.已知实数x,y满足
√x-2
+(y+1)2=0,则x-y等于( )- A. 3
- B. -3
- C. 1
- D. -1
5.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )
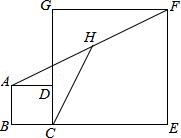

- A. 2.5
- B. √5
- C.
3 2 √2 - D. 2
6.如图,x轴、y轴上分别有两点A(3,0)、B(0,2),以点A为圆心,AB为半径的弧交x轴负半轴于点C,则点C的坐标为( )
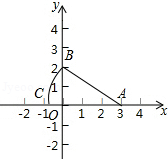
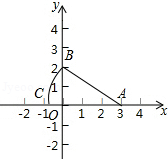
- A. (-1,0)
- B. (2-√5,0)
- C. (1-,0)√13
2 - D. (3-√13,0)
7.若顺次连接四边形各边中点所得的四边形是菱形,则该四边形一定是( )
- A. 矩形
- B. 一组对边相等,另一组对边平行的四边形
- C. 对角线相等的四边形
- D. 对角线互相垂直的四边形
8.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D'处,则点C的对应点C'的坐标为( )
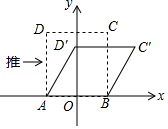

- A. (√3,1)
- B. (2,1)
- C. (1,√3)
- D. (2,√3)
9.如图,一根长25m的梯子,斜立在一竖直的墙上,这时梯足距离底端7m.如果梯子的顶端下滑4m,那么梯足将滑动( )


- A. 7m
- B. 8m
- C. 9m
- D. 10m
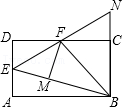
10.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:
①DF=CF;
②BF⊥EN;
③△BEN是等边三角形;
④S△BEF=3S△DEF.
其中,将正确结论的序号全部选对的是( )
①DF=CF;
②BF⊥EN;
③△BEN是等边三角形;
④S△BEF=3S△DEF.
其中,将正确结论的序号全部选对的是( )

- A. ①②③
- B. ①②④
- C. ②③④
- D. ①②③④
11.计算:(
√3
)2= ,√(-2)2
= ,√
= .| 4 |
| 3 |
12.若直角三角形的边长分别为3cm,4cm,则斜边上的中线长为 .
13.在菱形ABCD中,对角线AC=2,BD=4,则菱形ABCD的周长是 .
14.AD是△ABC的高,AB=4,AC=5,BC=6,则BD= .
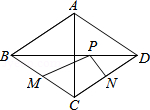
15.如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是 .

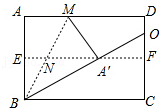
16.如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF;把纸片展平后再次折叠,使点A落在EF上的点A'处,得到折痕BM,BM与FF相交于点N.若直线BA'交直线CD于点O,BC=5,EN=1,则OD的长为 .

17.计算:
(1)(
(2)(6
.
(1)(
√48
-√75
)×√1
;| 1 |
| 3 |
(2)(6
√2
-4√6
)÷2√6
+(√5
-2)0-| 1 |
√3 |
18.已知a=
(1)a2-2ab+b2;
(2)a2-b2.
√7
+2,b=√7
-2,求下列代数式的值:(1)a2-2ab+b2;
(2)a2-b2.
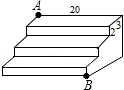
19.如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是多少?

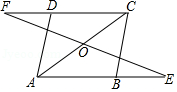
20.已知:如图,在平行四边形ABCD中,延长AB至点E,延长CD至点F,使得BE=DF.连接EF,与对角线AC交于点O.
求证:OE=OF.
求证:OE=OF.

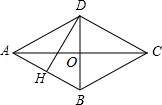
21.如图,四边形ABCD是菱形,对角线AC和BD相交于O点,DH垂直且平分AB,BD=8cm,求:DH,AC的长和菱形的面积.

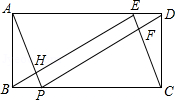
22.如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.
(1)判断△BEC的形状,并说明理由;
(2)求证:四边形EFPH是矩形.
(1)判断△BEC的形状,并说明理由;
(2)求证:四边形EFPH是矩形.

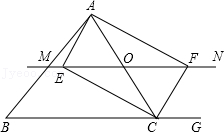
23.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN//BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.
(1)试说明EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.
(1)试说明EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.

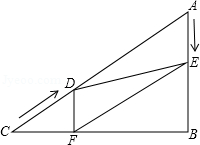
24.如图,在△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.






