试卷题目
1.二次根式
√x-2
在实数范围内有意义,则x的取值范围是( )- A. x>0
- B. x≥2
- C. x≥-2
- D. x≤2
2.下列各式中,正确的是( )
- A. =
a+2 a-2 a2-4 (a-2)2 - B. =
b a b+2 a+2 - C. =
b a+2b 1 a+2 - D. =-
-a+b c a+b c
3.一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒.当你抬头看信号灯时,是绿灯的概率是( )


- A.
1 12 - B.
1 3 - C.
5 12 - D.
1 2
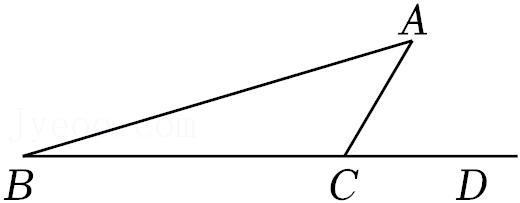
4.如图,已知∠ACD为∆ABC的外角,∠ACD=60°,∠B=20°,那么∠A的度数是( )

- A. 30°
- B. 40°
- C. 50°
- D. 60°
5.用直角三角板,作△ABC的高,下列作法正确的是( )
- A.

- B.

- C.

- D.

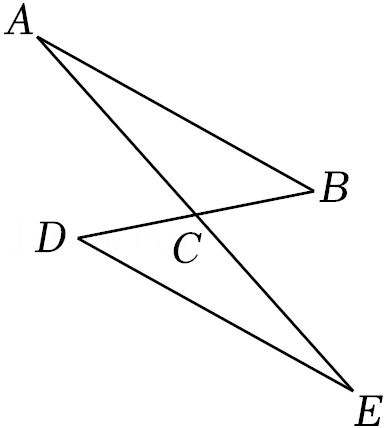
6.如图,线段AE、BD交于点C,AB=DE.请你添加一个条件,使得△ABC≌△EDC.你的选择是( )

- A. AB//DE
- B. AC=EC
- C. BC=DC
- D. ∠ACB=∠ECD
7.甲骨文是中国的一种古代文字,是汉字的早期形式,有时候也被认为是汉字的书体之一,也是现存中国王朝时期最古老的一种成熟文字.如图为甲骨文对照表中的部分文字,若把它们抽象为几何图形,其中最接近轴对称图形的甲骨文对应的汉字是( )

- A. 时
- B. 康
- C. 黄
- D. 奚
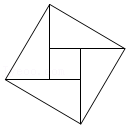
8.如图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”,它被第24届国际数学家大会选定为会徽,是国际数学界对我国古代数学伟大成就的肯定.“弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,若直角三角形的两条直角边分别为a、b,大正方形边长为3,小正方形边长为1,那么ab的值为( )

- A. 3
- B. 4
- C. 5
- D. 6
9.若分式
的值为0,则x= .
| x-2 |
| x+1 |
10.等腰三角形有两条边长为4cm和9cm,则该三角形的周长是 .
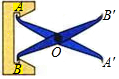
11.如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),在图中,要测量工件内槽宽AB,只要测量A′B′的长度即可,该做法的依据是 .

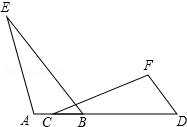
12.如今人们锻炼身体的意识日渐增强,但是发现少数人保护环境的意识仍显淡薄,应提醒注意.如图是房山某公园的一角,有人为了抄近道而避开路的拐角∠ABC(∠ABC=90°),于是在草坪内走出了一条不该有的“捷径路AC”.已知AB=30米,BC=40米,他们踩坏了 米的草坪,只为少走 米的路.


13.第24届冬季奥林匹克运动会将于2025年2月4日在北京开幕.小健通过统计数据了解到:从2002年到2018年的五届冬奥会上,中国队每届比赛均有金牌入账,共斩获了13枚金牌.于是,小健对同学们说:“2025年北京冬奥会中国队获得2枚以上金牌的可能性大小是100%”.你认为小健的说法 (填“合理”或“不合理” ),理由是 .
14.
=
+
是物理学中的一个公式,其中各个字母都不为零且R1+R2≠0.用R1,R2表示R,则R= .
| 1 |
| R |
| 1 |
| R1 |
| 1 |
| R2 |
15.如图,在△ABC中,AB=AC,D,E,F分别是BC,AC,AB上的点,且BF=CD,BD=CE,∠FDE=α,则∠A的度数是 度.(用含α的代数式表示)


16.等边△ABC的边长为2,P,Q分别是边AB,BC上的点,连结AQ,CP交于点O.以下结论:①若AP=BQ,则∠AOP=60°;②若AQ=CP,则∠AOC=120°;③若点P和点Q分别从点A和点C同时出发,以相同的速度向点B运动(到达点B就停止),则点O经过的路径长为
√3
.其中正确的是 (填序号).17.计算:
-
.
| y |
| 3x2 |
| 1 |
| 6xy |
18.计算:
√18
-3√27
+√12
÷√6
-√
.| 1 |
| 2 |
19.如图,点A、B、C、D在同一直线上,BE//DF,∠A=∠F,AB=FD.求证:AE=FC.

20.已知m2+3m-4=0,求代数式(m+2-
)÷
的值.
| 5 |
| m-2 |
| m-3 |
| m2-2m |
21.解分式方程:
-
=1.
| x |
| x-1 |
| 2 |
| x+1 |
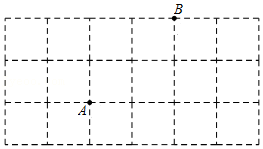
22.如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两个格点,如果点C也是图形中的格点,且△ABC为等腰三角形,请你在如下6×3的网格中找到所有符合条件的点C(可以用C1,C2…表示),并画出所有三角形.

23.王宇同学在几何学习过程中有一个发现:直角三角形中,如果有一个锐角是30°,那么这个锐角所对的直角边等于斜边的一半.
下面是他的探究发现过程,请你与他一起用尺规完成作图并补全证明过程(保留作图痕迹).
已知一条线段AB,分别以点A、B为圆心,以线段AB的长为半径画弧,两弧交于点C(点C在线段AB上方),作∠ACB的角平分线交AB于D.
由作图可知AB=CA=BC,
∴△ABC是 三角形,
∴∠ACB=60°( ),
∵CD平分∠ACB,
∴CD垂直平分AB( ),
∠DCB=
∠ACB=30°,
∴∠CDB=90°,BD=
AB,
又∵BC=AB,
∴BD=
BC,
即在Rt△DBC中,∠BDC=90°,∠DCB=30°,则BD=
BC.
下面是他的探究发现过程,请你与他一起用尺规完成作图并补全证明过程(保留作图痕迹).
已知一条线段AB,分别以点A、B为圆心,以线段AB的长为半径画弧,两弧交于点C(点C在线段AB上方),作∠ACB的角平分线交AB于D.
由作图可知AB=CA=BC,
∴△ABC是 三角形,
∴∠ACB=60°( ),
∵CD平分∠ACB,
∴CD垂直平分AB( ),
∠DCB=
| 1 |
| 2 |
∴∠CDB=90°,BD=
| 1 |
| 2 |
又∵BC=AB,
∴BD=
| 1 |
| 2 |
即在Rt△DBC中,∠BDC=90°,∠DCB=30°,则BD=
| 1 |
| 2 |
24.为了营造“创建文明城区、共享绿色家园”的良好氛围,房山某社区计划购买甲、乙两种树苗进行社区绿化.已知用1200元购买甲种树苗与用1000元购买乙种树苗的棵树相同,乙种树苗比甲种树苗每棵少20元,问甲种树苗每棵多少元?
25.口袋里有除颜色外其它都相同的6个红球和4个白球.
(1)先从袋子里取出m(m≥1)个白球,再从袋子里随机摸出一个球,将“摸出红球”记为事件A.
①如果事件A是必然事件,请直接写出m的值.
②如果事件A是随机事件,请直接写出m的值.
(2)先从袋子中取出m个白球,再放人m个一样的红球并摇匀,摸出一个球是红球的可能性大小是
,求m的值.
(1)先从袋子里取出m(m≥1)个白球,再从袋子里随机摸出一个球,将“摸出红球”记为事件A.
①如果事件A是必然事件,请直接写出m的值.
②如果事件A是随机事件,请直接写出m的值.
(2)先从袋子中取出m个白球,再放人m个一样的红球并摇匀,摸出一个球是红球的可能性大小是
| 4 |
| 5 |
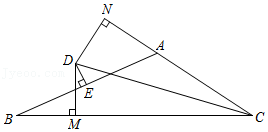
26.如图,△ABC中,CD平分∠ACB,DE⊥AB且E为AB中点,DM⊥BC于M,DN⊥AC于N,请你判断线段BM与AN的数量关系并加以证明.

27.数学课上,老师出示了一个题:如图,在△ABC中,∠ACB=90°,AC=5,AB=13,∠CAB的平分线交CB于点D,求CD的长.
晓涵同学思索了一会儿,考虑到角平分线所在直线是角的对称轴这一特点,于是构造了一对全等三角形,解决了这个问题.
请你在晓涵同学的启发下(或者独立思考后有自己的想法),解答这道题.

晓涵同学思索了一会儿,考虑到角平分线所在直线是角的对称轴这一特点,于是构造了一对全等三角形,解决了这个问题.
请你在晓涵同学的启发下(或者独立思考后有自己的想法),解答这道题.

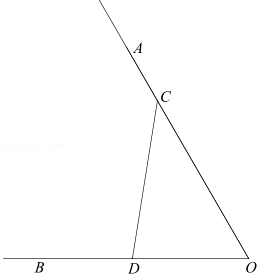
28.如图,∠AOB=60°,点C、D分别在射线OA、OB上,且满足OC=4.将线段DC绕点D顺时针旋转60°,得到线段DE.过点E作OC的平行线,交OB反向延长线于点F.
(1)根据题意完成作图;
(2)猜想DF的长并证明;
(3)若点M在射线OC上,且满足OM=3,直接写出线段ME的最小值.
(1)根据题意完成作图;
(2)猜想DF的长并证明;
(3)若点M在射线OC上,且满足OM=3,直接写出线段ME的最小值.