试卷题目
1.
√9
的平方根是( )- A. 3
- B. ±3
- C. √3
- D. ±√3
2.已知
是二元一次方程2x+y=3的一组解,则a的值是( )
| { |
|
- A. 1
- B. -1
- C. 2
- D. -2
3.如图,AF是∠BAC的平分线,DF∥AC,若∠1=25°,则∠BDF的度数为( )
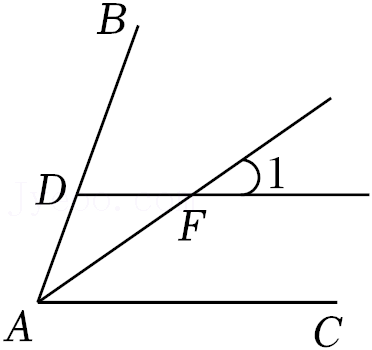

- A. 25°
- B. 50°
- C. 75°
- D. 100°
4.如图,在平面直角坐标系中,△ABC的顶点都在格点上,如果将△ABC先沿y轴翻折,再向上平移2个单位长度,得到△A'B'C',那么点B的对应点B'的坐标为( )
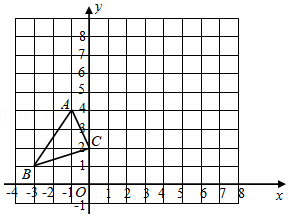

- A. (-3,3)
- B. (0,4)
- C. (3,3)
- D. (1,6)
5.已知点(x1,2),(x2,-4)都在直线y=-x+3上,则x1与x2的大小关系是( )
- A. x1>x2
- B. x1=x2
- C. x1<x2
- D. 不能比较
6.在学校的体育训练中,小杰投实心球的7次成绩就如统计图所示,则这7次成绩的中位数和众数分别是( )
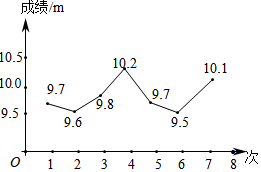

- A. 9.7m,9.8m
- B. 9.7m,9.7m
- C. 9.8m,9.9m
- D. 9.8m,9.8m
7.下列命题中:①相等的角是对顶角;②如果
+1=
,那么x=4;③两边分别相等且其中一组等边的对角相等的两个三角形全等;④三角形的内角和等于180°.其中是真命题的个数为( )
| x-5 |
| 2 |
| 3-x |
| 3 |
- A. 0个
- B. 1个
- C. 2个
- D. 3个
8.某公司上半年生产甲、乙两种型号的无人机若干架,已知甲种型号无人机架数比总架数的一半多11架,乙种型号无人机架数比总架数的三分之一少2架.设甲种型号无人机x架,乙种型号无人机y架,根据题意可列出的方程组是( )
- A.
{ x= (x+y)-111 3 y= (x+y)+21 2 - B.
{ x= (x+y)+111 3 y= (x+y)-21 2 - C.
{ x= (x+y)-111 2 y= (x+y)+21 3 - D.
{ x= (x+y)+111 2 y= (x+y)-21 3
9.函数y=bx与y=ax+b(a≠0,b≠0)在同一坐标系中的图象可能是( )
- A.

- B.

- C.

- D.

10.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b),则关于x,y的方程组
的解为( )
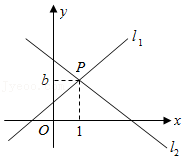
| { |
|

- A.
{ x=2 y=1 - B.
{ x=-2 y=1 - C.
{ x=1 y=4 - D.
{ x=1 y=2
11.如图所示,将分别含有30°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为75°,则图中∠α的度数为( )
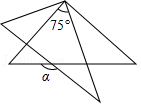

- A. 160°
- B. 150°
- C. 140°
- D. 130°
12.甲、乙两人分别从笔直道路上的A、B两地出发相向匀速而行,已知甲比乙先出发5分钟,两人在C地相遇,相遇后甲立即按原速原路返回A地,乙继续向A地前行,约定先到A地者停止运动就地休息.若甲、乙两人相距的路程y(米)与甲行走的时间x(分钟)之间的关系如图所示,有下列说法:①甲的速度是60米/分钟;②乙的速度是90米/分钟;③甲出发18分钟时,两人在C地相遇;④乙到达A地时,甲与A地相距460米,其中正确的说法有( )
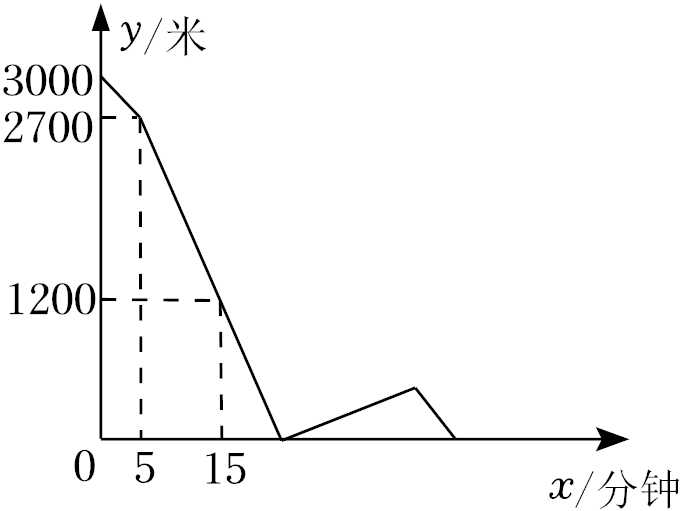

- A. ①②
- B. ①②③
- C. ①②④
- D. ①②③④
13.化简:
√14
÷√2
= .14.如图,如果※的位置为(3,1),则☆的位置是 .
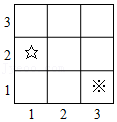

15.小明所在班级为希望工程捐款,他统计了全班同学的捐款情况,并绘制成如图所示的统计图,根据统计图,可计算出全班同学平均每人捐款 元.
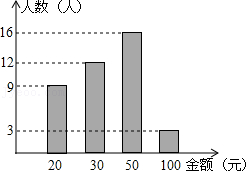

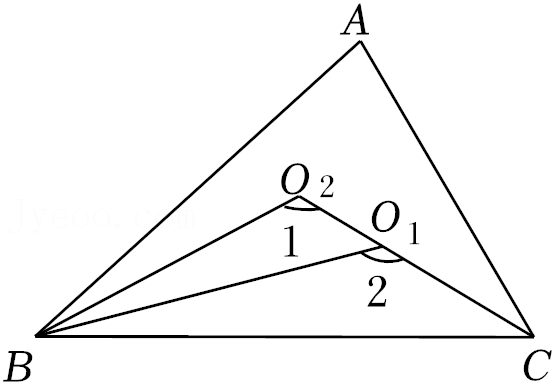
16.如图,△ABC中,∠ABC的三等分线分别与∠ACB的平分线交于点O1,O2,若∠1=115°,∠2=135°,则∠A的度数为 .

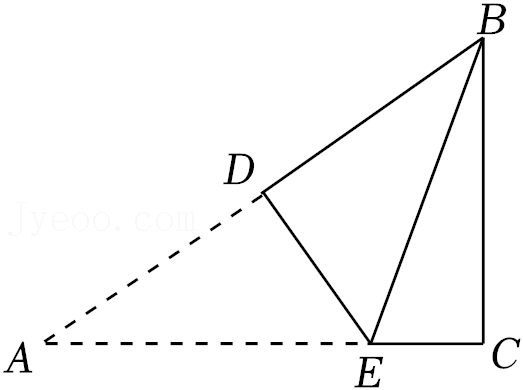
17.如图,已知△ABC中,∠C=90°,BC=3,AC=5,将此三角形沿DE翻折,使得点A与点B重合,则AE长为 .

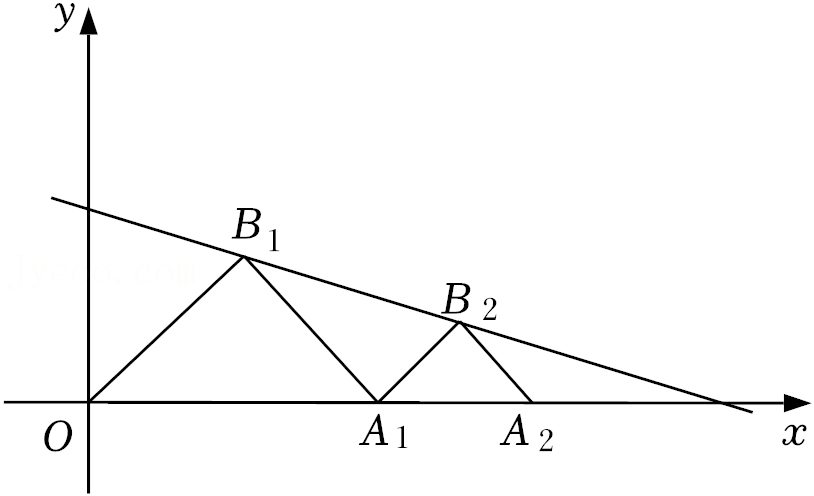
18.如图,△OA1B1,△A1A2B2都是斜边在x轴上的等腰直角三角形,点A1,A2都在x轴上,点B1,B2都在一次函数y=-
x+8(x>0)的图象上,则点B2的坐标为 .
| 1 |
| 3 |

19.计算:(
√6
+2)(√6
-2)-3√8
.20.解方程组:
.
| { |
|
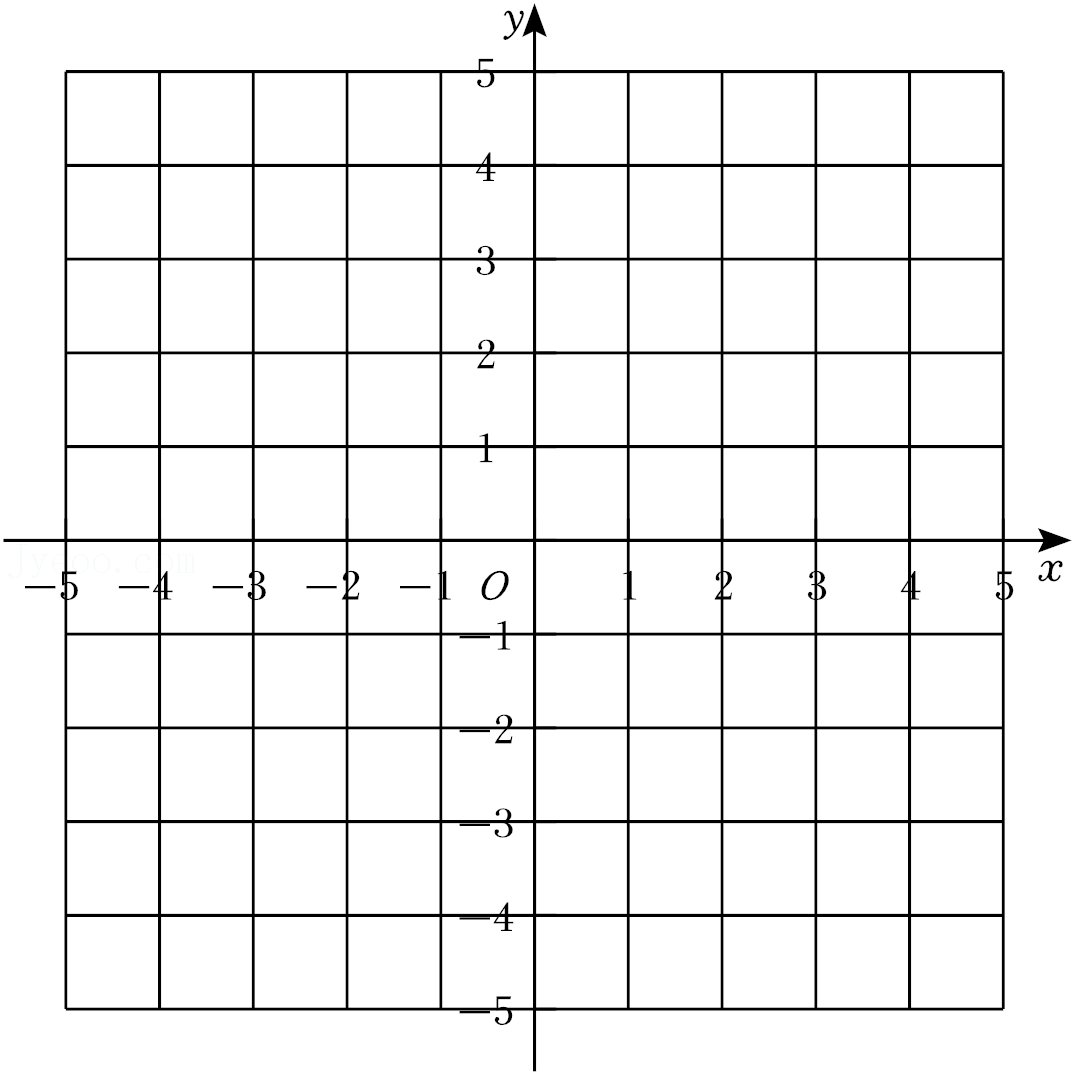
21.如图,在平面直角坐标系中.
(1)画出△ABC,其中A(1,-2),B(-2,4),C(2,2);
(2)画出△ABC关于x轴对称的△A1B1C1(其中A1、B1、C1分别为A、B、C的对应点);
(3)△ABC与△A1B1C1重合部分的面积为 .
(1)画出△ABC,其中A(1,-2),B(-2,4),C(2,2);
(2)画出△ABC关于x轴对称的△A1B1C1(其中A1、B1、C1分别为A、B、C的对应点);
(3)△ABC与△A1B1C1重合部分的面积为 .

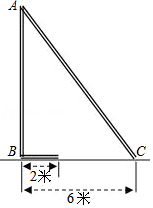
22.如图,小刚想知道学校旗杆的高度,他发现旗杆顶端A处的绳子垂到地面B处后还多2米.当他把绳子拉直并使下端刚好接触到地面C处,发现绳子下端到旗杆下端的距离为6米,请你帮小刚求出旗杆的高度AB长.

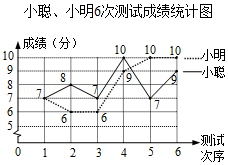
23.小聪、小明准备代表班级参加学校“团史知识”竞赛,班主任对这两名同学测试了6次,获得如图测试成绩折线统计图.根据图中信息,解答下列问题:
(1)根据上面的折线统计图,补全下列表格中的统计量:
a= ,b= ,c= ,d= ,e= ,f= .
(2)只结合小聪和小明成绩的平均数、中位数, 的数学成绩较好;只结合小聪和小明成绩的极差和方差, 的数学成绩较稳定.
(1)根据上面的折线统计图,补全下列表格中的统计量:
| 学生 | 平均数 | 中位数 | 众数 | 极差 | 方差 |
| 小聪 | 8 | b | c | 3 | f |
| 小明 | a | 8 | d | e | 3 |
a= ,b= ,c= ,d= ,e= ,f= .
(2)只结合小聪和小明成绩的平均数、中位数, 的数学成绩较好;只结合小聪和小明成绩的极差和方差, 的数学成绩较稳定.

24.某一天,蔬菜经营户王大叔花270元从蔬菜批发市场批发了黄瓜和茄子共70千克,到菜市场按零售价卖,黄瓜和茄子当天的批发价和零售价如下表所示:
(1)王大叔当天批发了黄瓜和茄子各多少千克?
(2)他卖完这些黄瓜和茄子共赚了多少元?
| 品名 | 黄瓜 | 茄子 |
| 批发价/(元/千克) | 5 | 3 |
| 零售价/(元/千克) | 7 | 4 |
(1)王大叔当天批发了黄瓜和茄子各多少千克?
(2)他卖完这些黄瓜和茄子共赚了多少元?
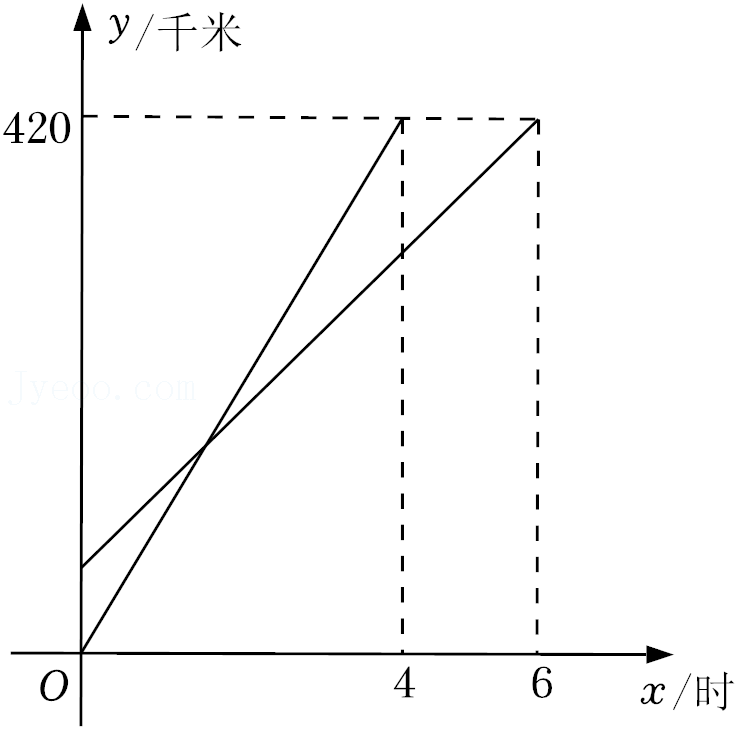
25.已知A、B两地相距420km,甲、乙两车均从A地向B地出发,乙车比甲车先出发1小时,两车分别以各自的速度匀速行驶,甲、乙两车距A地的路程y(千米)与甲车行驶所用的时间x(小时)的关系如图所示,结合图象信息回答下列问题:
(1)甲车的速度是 千米/时,乙车的速度是 千米/时;
(2)分别求出甲、乙两车距A地的路程y(千米)与它行驶所用的时间x(小时)之间的函数关系式;
(3)甲车出发多长时间后两车相距15千米?直接写出x的值.
(1)甲车的速度是 千米/时,乙车的速度是 千米/时;
(2)分别求出甲、乙两车距A地的路程y(千米)与它行驶所用的时间x(小时)之间的函数关系式;
(3)甲车出发多长时间后两车相距15千米?直接写出x的值.

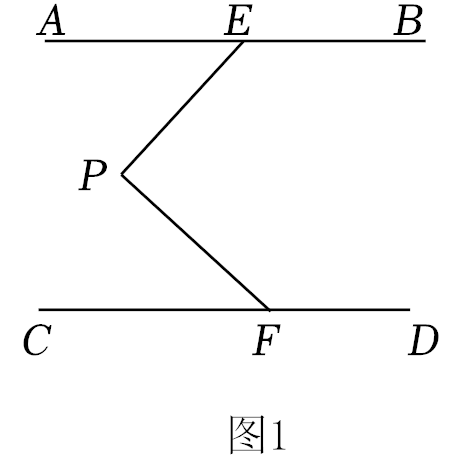
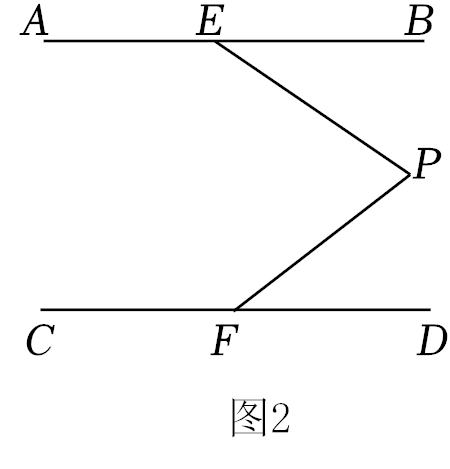
26.如图,AB∥CD,定点E,F分别在直线AB,CD上,在平行线AB,CD之间有一个动点P,满足0°<∠EPF<180°.
(1)试问:∠AEP,∠CFP,∠EPF满足怎样的数量关系?
解:由于点P是平行线AB,CD之间一动点,因此需对点P的位置进行分类讨论.
①如图1,当点P在EF的左侧时,猜想∠AEP,∠CFP,∠EPF满足的数量关系,并说明理由;
②如图2,当点P在EF的右侧时,直接写出∠AEP,∠CFP,∠EPF满足的数量关系为 .
(2)如图3,QE,QF分别平分∠PEB,∠PFD,且点P在EF左侧.
①若∠EPF=100°,则∠EQF的度数为 ;
②猜想∠EPF与∠EQF的数量关系,并说明理由.

(1)试问:∠AEP,∠CFP,∠EPF满足怎样的数量关系?
解:由于点P是平行线AB,CD之间一动点,因此需对点P的位置进行分类讨论.
①如图1,当点P在EF的左侧时,猜想∠AEP,∠CFP,∠EPF满足的数量关系,并说明理由;
②如图2,当点P在EF的右侧时,直接写出∠AEP,∠CFP,∠EPF满足的数量关系为 .
(2)如图3,QE,QF分别平分∠PEB,∠PFD,且点P在EF左侧.
①若∠EPF=100°,则∠EQF的度数为 ;
②猜想∠EPF与∠EQF的数量关系,并说明理由.



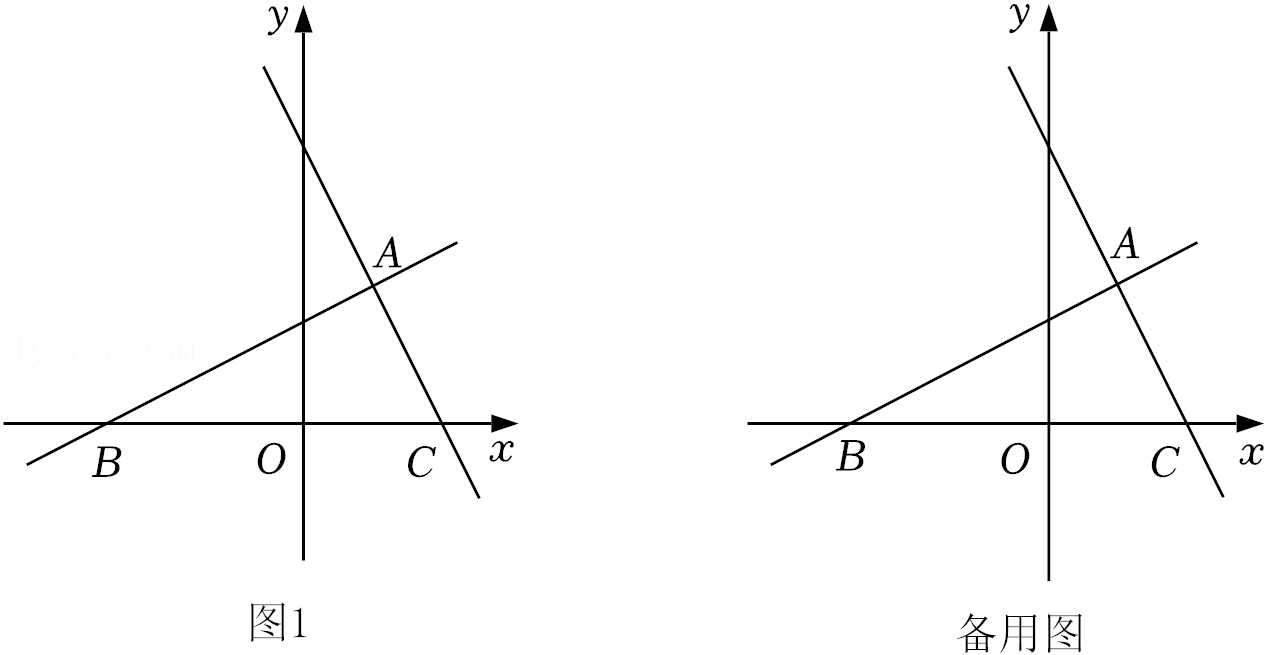
27.如图1,在平面直角坐标系xOy中,点O为坐标原点,直线AB:y=kx+
与直线AC:y=-2x+b交于点A,两直线与x轴分别交于点B(-3,0)和点C(2,0).
(1)求直线AB和AC的函数表达式;
(2)点P为y轴上一动点,当PA+PC最小时,求点P的坐标;
(3)点M为直线AC上一动点,当△ABM是等腰直角三角形时,请直接写出点M的坐标.
| 3 |
| 2 |
(1)求直线AB和AC的函数表达式;
(2)点P为y轴上一动点,当PA+PC最小时,求点P的坐标;
(3)点M为直线AC上一动点,当△ABM是等腰直角三角形时,请直接写出点M的坐标.






