试卷题目
1.下列各式一定为二次根式的是( )
- A. √x2-1
- B. √x
- C. √x2+1
- D. √x+1
2.下列运算结果正确的是( )
- A. 2√3+3√2=5√5
- B. 2√3×3√2=5√6
- C. √8÷√2=2
- D. √(-6)2=-6
3.如图所示,在数轴上点A所表示的数为a,则a的值为( )


- A. -1-√5
- B. 1-√5
- C. -√5
- D. -1+√5
4.已知平面直角坐标系内点P(1,2),Q(2,-3),那么线段PQ的长等于( )
- A. 5
- B. √26
- C. √27
- D. 2√7
5.下列说法正确的是( )
- A. 在一个直角三角形中,有两边的长度分别是3和5则第三边的长度一定是4
- B. 三边长度分别为1,1,√2的三角形是直角三角形,且1,1,√2是一组勾股数
- C. 三边长度分别是12,35,36的三角形是直角三角形
- D. 一个三角形的三边长分别为a,b,c,且a2-b2=c2,则这个三角形是直角三角形
6.实数a,b在数轴上的位置如图所示,则化简
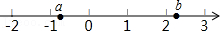
√(a-1)2
-√(a-b)2
+b的结果是( )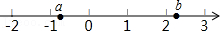
- A. 1
- B. b+1
- C. 2a
- D. 1-2a
7.按如图所示的程序计算,若开始输入的n值为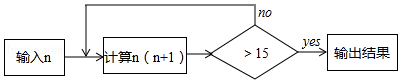
√2
,则最后输出的结果是( )
- A. 14
- B. 16
- C. 8+5√2
- D. 14+√2
8.如图,已知△ABC中,AB=
√10
,AC=3,BC=1,AB的垂直平分线分别交AC,AB于点D,E,连接BD,则CD的长为( )
- A.
3 2 - B.
4 3 - C. 1
- D.
3 4
9.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
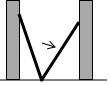

- A. 0.7米
- B. 1.5米
- C. 2.2米
- D. 2.4米
10.如图,圆柱形玻璃杯,高为12cm,底面周长为18cm.在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为( )cm.
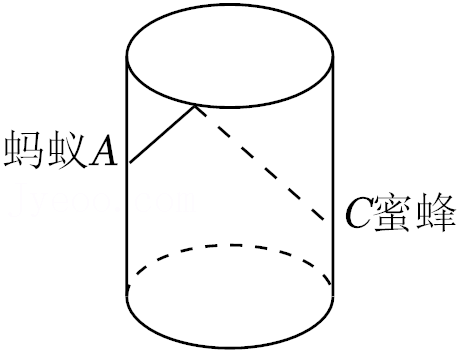

- A. 15
- B. √97
- C. 12
- D. 18
11.代数式
在实数范围内有意义,则x的取值范围是 .
√x-1 |
| x-2 |
12.如果最简二次根式
√2x+1
与√28
可以合并,则x= .13.已知x=2-
√3
,代数式(7+4√3
)x2+(2+√3
)x+√3
的值是 .14.如图所示的网格是正方形网格,则∠PAB+∠PBA= °(点A,B,P是网格线交点).
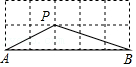

15.如图,在Rt△ABC的纸片中,∠C=90°,AC=5,AB=13.点D在边BC上,以AD为折痕将△ADB折叠得到△ADB′,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是 .
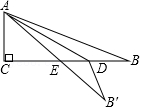

16.计算:
(1)2
÷3
(2)(2
(1)2
√12
×√3 |
| 4 |
√2
-(√8
-3√
);| 1 |
| 2 |
(2)(2
√3
-√6
)(2√3
+√6
)-(√3
+2)2.17.如图,在长度为1个单位的小正方形组成的网格中,点A,B,C小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′.
(2)△ABC的面积为 ;
(3)在直线l上找一点P,使PB+PC的长最短.(在图形中标出点P)

(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′.
(2)△ABC的面积为 ;
(3)在直线l上找一点P,使PB+PC的长最短.(在图形中标出点P)

18.先化简,再求值:
÷
-
,其中a=2-
| a2-b2 |
| a2-2ab+b2 |
| a+b |
| a-b |
| 2ab |
| a-b |
√3
,b=2+√3
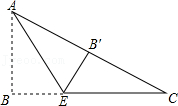
.19.如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,求EB′的长.

20.如图,在△ABC中,AD⊥BC,垂足为D,AD=4,BD=2,CD=8.
(1)求证:∠BAC=90°;
(2)P为BC边上一点,连接AP,若△ABP是以AB为腰的等腰三角形,请求出BP的长.

(1)求证:∠BAC=90°;
(2)P为BC边上一点,连接AP,若△ABP是以AB为腰的等腰三角形,请求出BP的长.

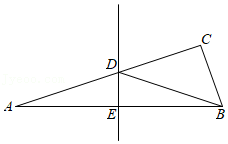
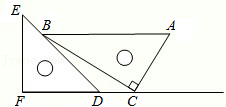
21.一副直角三角板如图放置,点C在FD延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10.
(1)求∠CBD的度数;
(2)试求CD的长.
(1)求∠CBD的度数;
(2)试求CD的长.

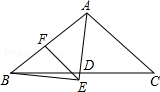
22.如图,在△ABC中,AD平分∠BAC交BC于点D,BE⊥AD,BE交AD的延长线于点E,点F在AB上,且EF∥AC,AE=3,AF=2.
(1)求BF的长度;
(2)求△ABE的面积.
(1)求BF的长度;
(2)求△ABE的面积.

23.学习了勾股定理和数的开方后,我们就能发现在部分特殊直角三角形中,直角边与斜边存在一些特殊的数量关系.例如:在等腰直角三角形中,两直角边相等,则有斜边平方等于一条直角边的平方的2倍,利用开方运算易得斜边是一条直角边的
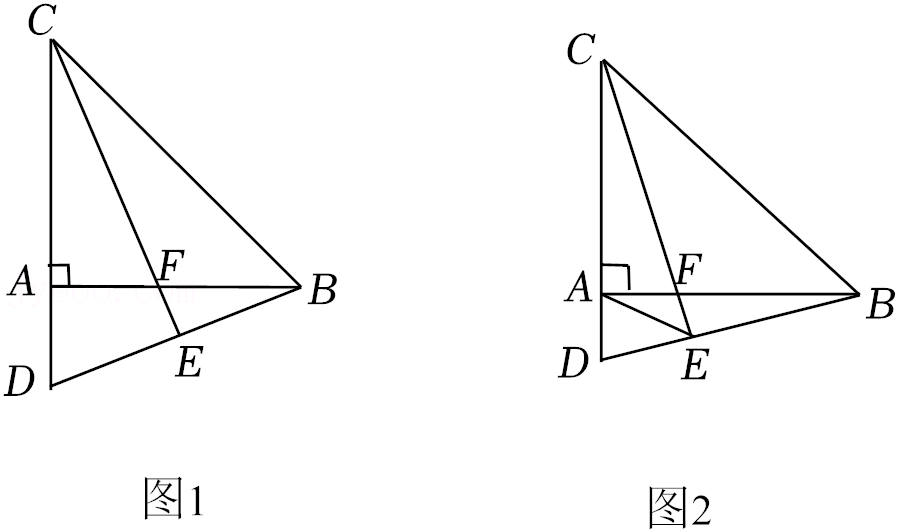
(1)如图1,若BC=6,则AC的长为 ;
(2)如图1,当点E是BD中点时,若BC=6,求AF的长;
(3)如图2,连接AE,判断线段DE+EF=
√2
倍,因此若要解决线段之间的√2
倍关系时,往往把问题放在等腰直角三角形中去思考;问题解决,如图CD⊥AB,垂足为A,且AB=AC,D是CA延长线上一点,连接BD,点E是线段BD上的一点,连接CE交AB于点F,且BD=CF.(1)如图1,若BC=6,则AC的长为 ;
(2)如图1,当点E是BD中点时,若BC=6,求AF的长;
(3)如图2,连接AE,判断线段DE+EF=
√2
AE是否成立?若成立,请证明你的结论;若不成立,请说明理由.





