试卷题目
1.平面直角坐标系中,点P(-2,3)关于x轴对称的点的坐标为( )
- A. (-2,-3)
- B. (2,-3)
- C. (-3,-2)
- D. (3,-2)
2.计算(-3x)3的结果是( )
- A. -27x3
- B. -9x3
- C. 9x3
- D. 27x3
3.北京是首批国家历史文化名城和世界上拥有世界文化遗产数最多的城市,三千多年的历史孕育了众多名胜古迹,让每一个中国人为之骄傲.如图是一些北京名胜古迹的标志,其中不属于轴对称图形的是( )
- A.

天坛 - B.

圆明园 - C.

颐和园 - D.

天安门
4.正多边形的一个外角的度数为36°,则这个正多边形的边数为( )
- A. 6
- B. 8
- C. 10
- D. 12
5.已知直角三角形中30°角所对的直角边为2cm,则斜边的长为( )
- A. 2cm
- B. 4cm
- C. 6cm
- D. 8cm
6.用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( )
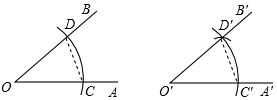

- A. SAS
- B. AAS
- C. ASA
- D. SSS
7.如图,在△ABC和△ADC中,∠B=∠D=90°,CB=CD,∠1=30°,则∠2=( )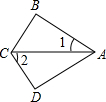

- A. 30°
- B. 40°
- C. 50°
- D. 60°
8.下列计算,正确的是( )
- A. a6÷a3=a2
- B. b3•b3=b9
- C. x2+x2=2x2
- D. (m2)3=m5
9.如图,已知△ABC中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )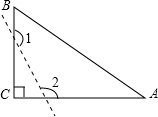

- A. 90°
- B. 135°
- C. 270°
- D. 315°
10.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )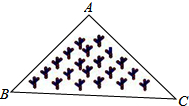

- A. △ABC的三条中线的交点
- B. △ABC三条角平分线的交点
- C. △ABC三条高所在直线的交点
- D. △ABC三边的中垂线的交点
11.要使分式
有意义,则x的取值范围是 .
| 5 |
| x-3 |
12.等腰三角形腰AB=10,底边BC=12,则△ABC的周长为 .
13.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y= .
14.把多项式m3-16m分解因式的结果是 .
15.计算:(
)-2+(-3)0= .
| 1 |
| 2 |
16.已知D、E分别是△ABC的边BC和边AC的中点,连接DE、AD,若S△ABC=24cm2,则S△DEC= .

17.若5x=2,5y=3,则5x+2y= .
18.(1)计算:(-2ab2)2-4ab3(ab+1);
(2)解方程:
+1=
.
(2)解方程:
| x-3 |
| x-2 |
| 3 |
| 2-x |
19.若△ABC的三边长分别为m-2,2m+1,8.
(1)求m的取值范围;
(2)若△ABC的三边均为整数,求△ABC的周长.
(1)求m的取值范围;
(2)若△ABC的三边均为整数,求△ABC的周长.
20.先化简,再求值:(x-2y)2-(x-y)(x+y)-5y2,其中x=
,y=-3.
| 1 |
| 4 |
21.已知:在△ABC中,AD是BC边上的高.
(1)尺规作图:作∠BAC的平分线AE,交BC于点E;
(2)在(1)的条件下:若∠ABC=105°,∠C=45°,求∠EAD的度数.
(1)尺规作图:作∠BAC的平分线AE,交BC于点E;
(2)在(1)的条件下:若∠ABC=105°,∠C=45°,求∠EAD的度数.







