试卷题目
1.二次根式
√x-1
在实数范围内有意义,则实数x的取值范围是( )- A. x≥-1
- B. x≠0
- C. x≥1
- D. x>0
2.下列计算正确的是( )
- A. (a3)2=a5
- B. a6÷a2=a3
- C. a7•a-4=a3
- D. (a-2)-3=a-6
3.下列分式中,是最简分式的是( )
- A.
2(x+1) x+1 - B.
a-b a+b - C.
2ax 3ay - D.
a2-b2 a-b
4.下列计算正确的是( )
- A. (2√2)2=4√2
- B. √2×√3=√6
- C. √2+√3=√5
- D. √12÷√3=4
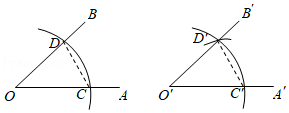
5.尺规作图:作∠A'O'B'角等于已知角∠AOB.示意图如图所示,则说明∠A'O'B'=∠AOB的依据是( )

- A. SSS
- B. SAS
- C. ASA
- D. AAS
6.在3.14,0,-
,
,2.010010001…(每两个1之间的0依次增加1个)这六个数中,无理数有( )
| π |
| 5 |
√2
,-| 1 |
| 4 |
- A. 2个
- B. 3个
- C. 4个
- D. 5个
7.在数轴上表示某不等式组的解集,如图所示,则这个不等式组可能是( )


- A.
{ 2x-4>x x+1≥0 - B.
{ 2x-4>x x+1≤0 - C.
{ 2x-4<x x+1≤0 - D.
{ 2x-4<x x+1≥0
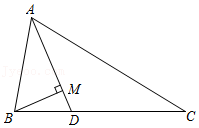
8.如图,在△ABC中,AD为∠BAC的平分线,BM⊥AD,垂足为M,且AB=5,BM=2,AC=9,则∠ABC与∠C的关系为( )

- A. ∠ABC=2∠C
- B. ∠ABC=∠C
5 2 - C. ∠ABC=∠C
1 4 - D. ∠ABC=3∠C
9.81的算术平方根是 .
10.生物学家发现一种病毒的长度约为0.000063毫米,用科学记数法表示为 毫米.
11.不等式3x-5>1的最小整数解是 .
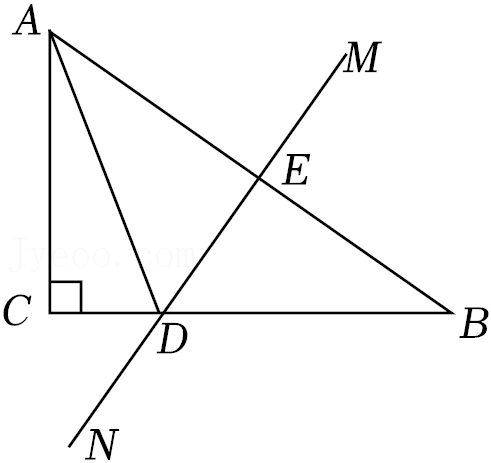
12.如图,在△ABC中,∠C=90°,∠B=35°,线段AB的垂直平分线MN与AB交于点E,与BC交于点D,连接AD,则∠DAC= 度.

13.当a=3
√2
,b=√8
时,则a+b的值为 .14.若关于x的方程
=
有增根,则m的值是 .
| x+1 |
| x-2 |
| m |
| x-2 |
15.用海伦公式求面积的计算方法是:S=
.我国宋代数学家秦九韶提出的“三斜求积术”与这个公式基本一致,所以这个公式也叫“海伦-秦九韶公式”.请你利用公式解答下列问题.在△ABC中,已知三边之长a=6,b=7,c=5,则△ABC的面积为 .
√p(p-a)(p-b)(p-c)
,其中S表示三角形的面积,a,b,c分别表示三边之长,p表示周长的一半,即p=| a+b+c |
| 2 |
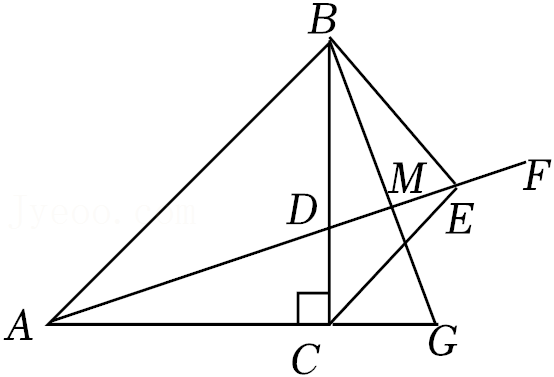
16.如图,在Rt△ABC中,∠ACB=90°,AC=BC,射线AF是∠BAC的平分线,交BC于点D,过点B作AB的垂线与射线AF交于点E,连结CE,M是DE的中点,连结BM并延长与AC的延长线交于点G.则下列结论正确的是 .
①△BCG≌△ACD;②BG垂直平分DE;③BE⊥CE;④∠G=2∠GBE;⑤BE+CG=AC.
①△BCG≌△ACD;②BG垂直平分DE;③BE⊥CE;④∠G=2∠GBE;⑤BE+CG=AC.

17.计算:-12+(
)-1
√3
-1)0+√16
-(| 1 |
| 2 |
18.求不等式组
的解集.
| { |
|
19.先化简
÷(1+
),再从-1<x<2的范围内选取一个合适的整数代入求值.
| x+1 |
| 1-x |
| x2+x |
| 1-x2 |
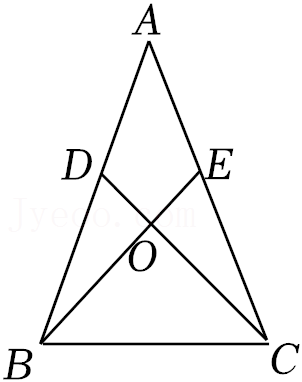
20.如图,△ABC中,AB=AC,D、E分别是AB、AC上的点,且∠ABE=∠ACD,连结BE、CD交于点O,求证:△OBC是等腰三角形.

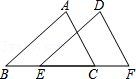
21.已知:如图,点E,C在线段BF上,AC=DF,AC∥DF,BE=CF.求证:AB∥DE.

22.今年4月23日是第26个世界读书日.八(1)班举办了“让读书成为习惯,让书香飘满校园”主题活动.准备订购一批新的图书鲁迅文集(套)和四大名著(套).
(1)采购员从市场上了解到四大名著(套)的单价比鲁迅文集(套)的单价的贵25元.花费1000元购买鲁迅文集(套)的数量与花费1500元购买四大名著(套)的数量相同.求鲁迅文集(套)和四大名著(套)的单价各是多少元?
(2)若购买鲁迅文集和四大名著共10套(两类图书都要买),总费用不超过570元,问该班有哪几种购买方案?
(1)采购员从市场上了解到四大名著(套)的单价比鲁迅文集(套)的单价的贵25元.花费1000元购买鲁迅文集(套)的数量与花费1500元购买四大名著(套)的数量相同.求鲁迅文集(套)和四大名著(套)的单价各是多少元?
(2)若购买鲁迅文集和四大名著共10套(两类图书都要买),总费用不超过570元,问该班有哪几种购买方案?
23.王老师让同学们根据二次根式的相关内容编写一道题,以下是王老师选出的两道题和她自己编写的一道题.先阅读,再回答问题.
(1)小青编的题,观察下列等式:
=
=
=
=
=
=
=
=
直接写出以下算式的结果:
= ;
(n为正整数)= ;
(2)小明编的题,由二次根式的乘法可知:
(
再根据平方根的定义可得:
直接写出以下算式的结果:
(3)王老师编的题,根据你的发现,完成以下计算:
(
+
+
+
+
)•
(1)小青编的题,观察下列等式:
| 2 |
√3 +1 |
| 2( √3 -1) |
| ( √3 +1)(√3 -1) |
| 2( √3 -1) |
| ( √3 )2-12 |
| 2( √3 -1) |
| 3-1 |
√3
-1;| 2 |
√5 +√3 |
| 2( √5 -√3 ) |
| ( √5 +√3 )(√5 -√3 ) |
| 2( √5 -√3 ) |
| ( √5 )2-(√3 )2 |
| 2( √5 -√3 ) |
| 5-3 |
√5
-√3
;直接写出以下算式的结果:
| 2 |
√7 +√5 |
| 2 |
√2n+1 +√2n-1 |
(2)小明编的题,由二次根式的乘法可知:
(
√3
+1)2=4+2√3
,(√5
+√3
)2=8+2√15
,(√a
+√b
)2=a+b+2√ab
(a≥0,b≥0);再根据平方根的定义可得:
√4+2
=√3
√3
+1,√8+2
=√15
√5
+√3
,√a+b+2
=√ab
√a
+√b
(a≥0,b≥0);直接写出以下算式的结果:
√6+2
= ,√5
√4-2
= ,√3
√7+4
= ;√3
(3)王老师编的题,根据你的发现,完成以下计算:
(
| 2 |
√3 +1 |
| 2 |
√5 +√3 |
| 2 |
√7 +√5 |
| 2 |
√9 +√7 |
| 2 |
√11 +√9 |
√12+2
.√11
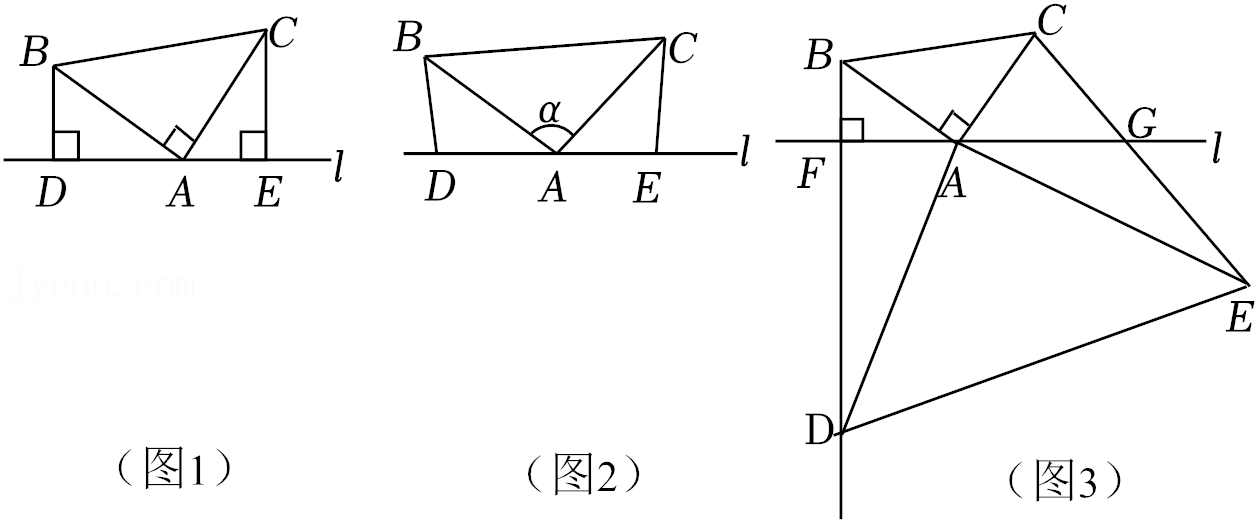
24.直线l经过点A,△ABC在直线l上方,AB=AC.
(1)如图1,∠BAC=90°,过点B,C作直线l的垂线,垂足分别为D、E.求证:△ABD≌△CAE;
(2)如图2,D,A,E三点在直线l上,若∠BAC=∠BDA=∠AEC=α(α为任意锐角或钝角),猜想线段DE、BD、CE有何数量关系?并给出证明;
(3)如图3,∠BAC=90°过点B作直线l上的垂线,垂足为F,点D是BF延长线上的一个动点,连结AD,作∠DAE=90°,使得AE=AD,连结DE,CE.直线l与CE交于点G.求证:G是CE的中点.
(1)如图1,∠BAC=90°,过点B,C作直线l的垂线,垂足分别为D、E.求证:△ABD≌△CAE;
(2)如图2,D,A,E三点在直线l上,若∠BAC=∠BDA=∠AEC=α(α为任意锐角或钝角),猜想线段DE、BD、CE有何数量关系?并给出证明;
(3)如图3,∠BAC=90°过点B作直线l上的垂线,垂足为F,点D是BF延长线上的一个动点,连结AD,作∠DAE=90°,使得AE=AD,连结DE,CE.直线l与CE交于点G.求证:G是CE的中点.






