试卷题目
1.中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹,用于装点生活或配合其他民俗活动的民间艺术.2006年5月20日,剪纸艺术遗产经国务院批准列入第一批国家级非物质文化遗产名录.2009年9月28日至10月2日举行的联合国教科文组织保护非物质文化遗产政府间委员会第四次会议上,中国申报的中国剪纸项目入选“人类非物质文化遗产代表作名录”.下列四个剪纸图案是轴对称图形的为( )
- A.

- B.

- C.

- D.

2.雾是由悬浮在大气中微小液滴构成的气溶胶,雾滴的直径多为0.000004m~0.00003m.其中,0.000004用科学记数法表示为( )
- A. 4×106
- B. 4×107
- C. 4×10-6
- D. 4×10-7
3.下列计算正确的是( )
- A. a3•a2=a
- B. a3•a2=a5
- C. a3•a2=a6
- D. a3•a2=a9
4.要使分式
有意义, 则x的取值范围是( )
| 3 |
| x-2 |
- A. x>2
- B. x<2
- C. x≠2
- D. x≠-2
5.下列等式中,从左到右的变形是因式分解的是( )
- A. a(a-3)=a2-3a
- B. (a+3)2=a2+6a+9
- C. 6a2+1=a2(6+)
1 a2 - D. a2-9=(a+3)(a-3)
6.已知:如图,在△ABC中,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E.若∠CAB=30°,AB=6,则DE+DB的值为( )
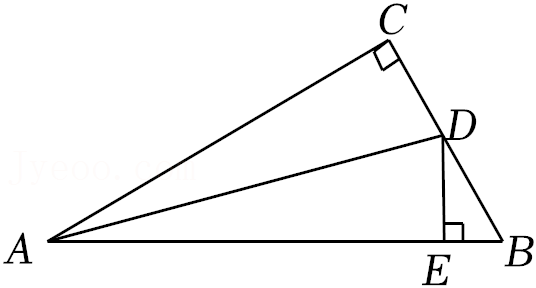

- A. 2
- B. 3
- C. 4
- D. 5
7.如图,是多功能扳手和各部分功能介绍的图片.阅读功能介绍,计算图片中∠α的度数为( )


- A. 60°
- B. 120°
- C. 135°
- D. 150°
8.小举在探究全等三角形判定方法,已知如图,△ABC,他通过尺规作图、裁剪、重合的操作,证实一种判定方法.以下是小举的操作过程:
第一步:尺规作图.
作法:(1)作射线B'M;
(2)以点B为圆心,任意长为半径画弧,分别交BA,BC于点E,D;
(3)以点B'为圆心,BD长为半径画弧,交B'M于点P;
(4)以点P为圆心,DE长为半径画弧,在B'M的上方交(3)中所画弧于点Q;
(5)过点Q作射线B'N;
(6)以点B'为圆心,BC长为半径画弧,交B'M于点C';
(7)以点B'为圆心,BA长为半径画弧,交B'N于点A';
(8)连接A'C'.
第二步:把作出的△A'B'C'剪下来,放到△ABC上.
第三步:观察发现△A'B'C'和△ABC重合.
∴△ABC≌△A'B'C'.
根据小举的操作过程可知,小举是在探究( )
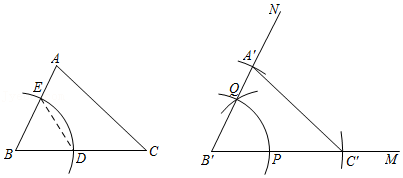
第一步:尺规作图.
作法:(1)作射线B'M;
(2)以点B为圆心,任意长为半径画弧,分别交BA,BC于点E,D;
(3)以点B'为圆心,BD长为半径画弧,交B'M于点P;
(4)以点P为圆心,DE长为半径画弧,在B'M的上方交(3)中所画弧于点Q;
(5)过点Q作射线B'N;
(6)以点B'为圆心,BC长为半径画弧,交B'M于点C';
(7)以点B'为圆心,BA长为半径画弧,交B'N于点A';
(8)连接A'C'.
第二步:把作出的△A'B'C'剪下来,放到△ABC上.
第三步:观察发现△A'B'C'和△ABC重合.
∴△ABC≌△A'B'C'.
根据小举的操作过程可知,小举是在探究( )
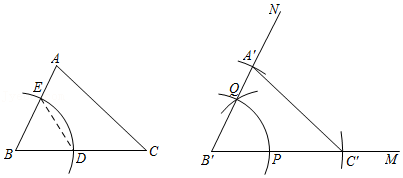
- A. 基本事实SSS
- B. 基本事实ASA
- C. 基本事实SAS
- D. 定理AAS
9.2021年6月,怀柔区政府和内蒙古自治区四子王旗政府签订了《2021年东西部协作协议》,在乡村振兴、产业合作、消费帮扶、就业帮扶、教育和健康帮扶方面,按计划推动工作落实.在产业合作过程中,怀柔区为四子王旗提供设备和技术支持,运送设备使用大货车,技术人员乘坐面包车.已知怀柔区与四子王旗相距600千米,若面包车的速度是大货车的1.2倍,两车同时从怀柔区出发,大货车到达四子王旗比面包车多用
小时.求大货车和面包车的速度.设大货车速度为x千米/小时,下面是四位同学所列的方程:
①国国:
=
+
;②佳佳:
+
=
;
③富富:
=
-
;④强强:
-
=
.
其中,正确的序号是( )
| 4 |
| 3 |
①国国:
| 600 |
| x |
| 600 |
| 1.2x |
| 4 |
| 3 |
| 4 |
| 3 |
| 600 |
| x |
| 600 |
| 1.2x |
③富富:
| 600 |
| x |
| 600 |
| 1.2x |
| 4 |
| 3 |
| 600 |
| x |
| 4 |
| 3 |
| 600 |
| 1.2x |
其中,正确的序号是( )
- A. ①②
- B. ①③
- C. ①④
- D. ②③
10.在平面直角坐标系xOy中,点A的坐标为(0,2),点B的坐标为(2
√3
,0),点C在x轴上.若△ABC为等腰三角形时,∠ABC=30°,则点C的坐标为( )- A. (-2√3,0),(,0),(2
2 √33 √3-4,0) - B. (-2√3,0),(,0),(4+2√3
3 √3,0) - C. (-2√3,0),(,0),(
2 √33 ,0)√33 - D. (-2√3,0),(1,0),(4-2√3,0)
11.计算:(2ab2)3= .
12.约分:
= .
| 2x2 |
| 10xy |
13.已知三角形的两边长分别是4和6,则第三条边长x的取值范围是 .
14.-
=
| 2a |
| b2 |
| 2a |
| ( ) |
15.已知:如图,AB=DB.只需添加一个条件即可证明△ABC≌△DBC.这个条件可以是 .(写出一个即可)
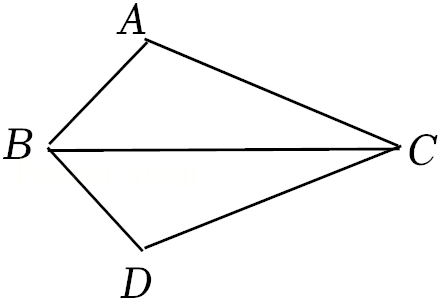

16.如图,∠MOP=60°,OM=5,动点N从点O出发,以每秒1个单位长度的速度沿射线OP运动.设点N的运动时间为t秒,当△MON是锐角三角形时,t满足的条件是 .


17.计算:(
|-(-
)2
√2
)0-(-3)-2+|-| 1 |
| 9 |
| 1 |
| 3 |
18.分解因式:2a2-8ab+8b2
19.已知2a2+a-6=0,求代数式(3a+2)(3a-2)-(5a3-2a2)÷a的值.
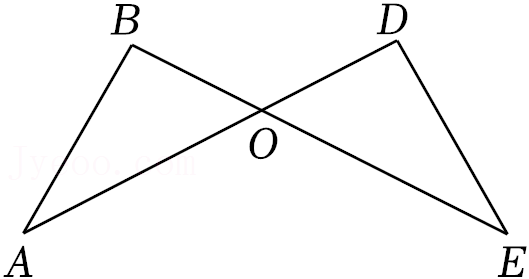
20.已知:如图,AD,BE相交于点O,AB⊥BE,DE⊥AD,垂足分别为B,D,OA=OE.求证:△ABO≌△EDO.

21.老师布置了如下尺规作图的作业:
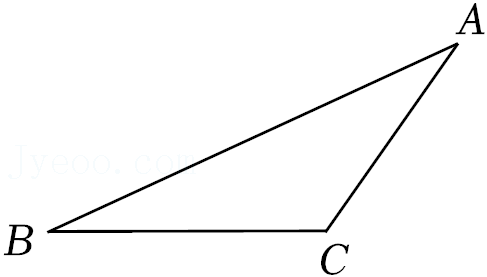
已知:如图△ABC.
求作:△ABC边BC上的高AM.
下面是小红设计的尺规作图过程:
作法:
①延长线段BC;
②以点A为圆心,AC长为半径作弧交BC的延长线于点D;
③分别以点C,D为圆心,大于
CD的长为半径作弧,两弧在CD下方交于点E;
④连接AE,交CD于点M.
所以线段AM就是所求作的高线.
根据小红设计的尺规作图过程和图形,完成(1)(2)两小题:
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)将该作图证明过程补充完整:
由②可得:AC= .
由③可得: .
∴( ).(填推理的依据)
即AM是△ABC边BC上的高线.
已知:如图△ABC.
求作:△ABC边BC上的高AM.
下面是小红设计的尺规作图过程:
作法:
①延长线段BC;
②以点A为圆心,AC长为半径作弧交BC的延长线于点D;
③分别以点C,D为圆心,大于
| 1 |
| 2 |
④连接AE,交CD于点M.
所以线段AM就是所求作的高线.
根据小红设计的尺规作图过程和图形,完成(1)(2)两小题:
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)将该作图证明过程补充完整:
由②可得:AC= .
由③可得: .
∴( ).(填推理的依据)
即AM是△ABC边BC上的高线.

22.解分式方程:
-
=0
| 5 |
| x-2 |
| 3 |
| x |
23.计算:(
-
)÷[(6x+4)÷x]
| x+2 |
| x2-2x |
| 1 |
| x+2 |
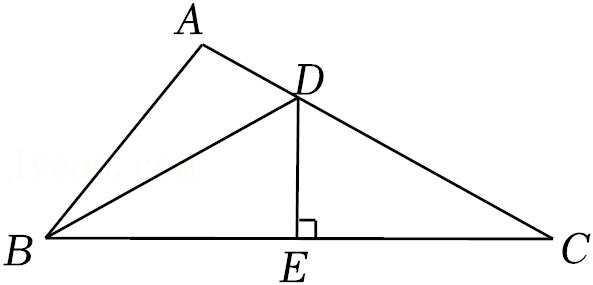
24.如图,在△ABC中,DE垂直平分BC,垂足为E,交AC于点D,连接BD.若∠A=100°,∠ABD=22°,求∠C的度数.

25.我们知道,假分数可以化为整数与真分数的和的形式.例如:
=1+
.在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,称之为“假分式”;当分子的次数小于分母的次数时,称之为“真分式”.例如:像
,
,…,这样的分式是假分式;像
,
,…,这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式.
例如:
=
=1+
;
=
=x+1+
.
解决下列问题:
(1)写出一个假分式为: ;
(2)将分式
化为整式与真分式的和的形式为: ;(直接写出结果即可)
(3)如果分式
的值为整数,求x的整数值.
| 5 |
| 4 |
| 1 |
| 4 |
| x+5 |
| x+2 |
| x2 |
| x-1 |
| 3 |
| x-4 |
| x |
| x2-1 |
例如:
| x+5 |
| x+2 |
| (x+2)+3 |
| x+2 |
| 3 |
| x+2 |
| x2 |
| x-1 |
| (x+1)(x-1)+1 |
| x-1 |
| 1 |
| x-1 |
解决下列问题:
(1)写出一个假分式为: ;
(2)将分式
| x+1 |
| x-3 |
(3)如果分式
| x2-x |
| x-2 |
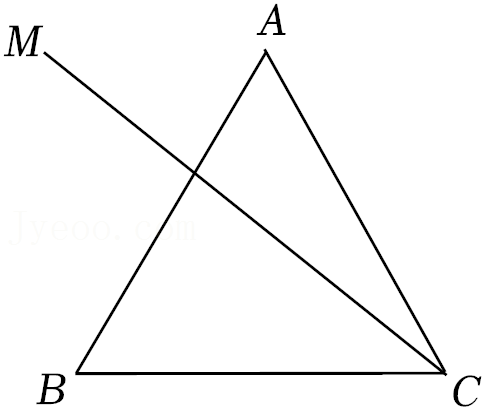
26.如图,在等边三角形ABC边AC左侧有一射线CM,∠ACM=α(0°<α<30°),点A关于射线CM的对称点为点E,连接BE并延长交CM于点N,连接AN,AE,CE.
(1)依题意补全图形;
(2)在α(0°<α<30°)的变化过程中,
①求∠BEC的大小(用含α的代数式表示);
②∠ANC的大小是否发生变化?如果发生变化,请直接写出变化的范围;如果不发生变化,请直接写出∠ANC的大小;
(3)用等式表示线段AN,BE,NC之间的数量关系.
(1)依题意补全图形;
(2)在α(0°<α<30°)的变化过程中,
①求∠BEC的大小(用含α的代数式表示);
②∠ANC的大小是否发生变化?如果发生变化,请直接写出变化的范围;如果不发生变化,请直接写出∠ANC的大小;
(3)用等式表示线段AN,BE,NC之间的数量关系.

27.在平面直角坐标系xOy中,点M(2,t-2)与点N关于过点(0,t)且垂直于y轴的直线对称.
(1)当t=-3时,点N的坐标为 ;
(2)以MN为底边作等腰三角形MNP.
①当t=1且直线MP经过原点O时,点P坐标为
②若△MNP上所有点到x轴的距离都不小于a(a是正实数),则t的取值范围是 (用含a的代数式表示).
(1)当t=-3时,点N的坐标为 ;
(2)以MN为底边作等腰三角形MNP.
①当t=1且直线MP经过原点O时,点P坐标为
②若△MNP上所有点到x轴的距离都不小于a(a是正实数),则t的取值范围是 (用含a的代数式表示).





