试卷题目
1.要使分式
有意义,则x的取值范围是( )
| 1 |
| x-2 |
- A. x≠2
- B. x≥-2
- C. x≥2
- D. x≠-2
2.下列二次根式中,是最简二次根式的是( )
- A. √0.5
- B. √12
- C. √
1 3 - D. √30
3.在数轴上表示不等式x+5>1的解集,正确的是( )
- A.

- B.

- C.

- D.

4.若分式
的值为5,则x、y同时扩大2倍,分式的值是( )
| 3y |
| x-y |
- A. 不变
- B. 扩大5倍
- C. 缩小5倍
- D. 不存在
5.一个等腰三角形两边长分别为2、5,则这个等腰三角形的周长为( )
- A. 9
- B. 12
- C. 9或12
- D. 11或12或13
6.如图,已知△ABC的外角∠CAD=120°,∠C=80°,则∠B的度数是( )


- A. 30°
- B. 40°
- C. 50°
- D. 60°
7.下列计算中,正确的是( )
- A. (0.1)-3=0.0001
- B. (2π-6.28)0=1
- C. (10-5×2)0=1
- D. (2021)-1=2021
8.下列命题为假命题的是( )
- A. 三角形的三个内角的和等于180度
- B. 三角形的任意两边之和大于第三边
- C. 三角形的角平分线是一条射线
- D. 三角形的面积等于一条边上的长与该条边上的高的乘积的一半
9.北起张家界,南至怀化,串起张家界、芙蓉镇、古丈、凤凰古城等众多著名风景区,被誉为“湘西最美高铁”的张吉怀高铁于2021年12月6日正式开通运营.线路全长245千米,已知高铁的平均速度是普通列车的3倍,相较于以往普通列车时间上节约3小时,设普通列车的时速是xkm/h,据题意,下列方程正确是( )
- A. -
245 3x =3245 x - B. -
245 x =3245 3x - C. -
245 3x =3245 x1 3 - D. -
245 x1 3 =3245 x
10.如图,△ABC是等边三角形,点P在△ABC内,PA=6,将△PAB绕点A逆时针旋转得到△QAC,则PQ的长等于( )
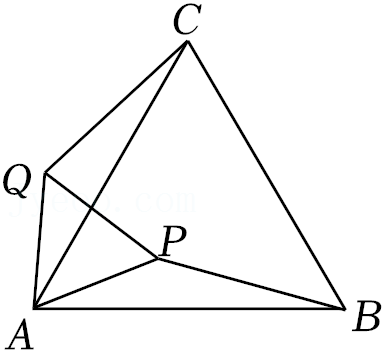

- A. 6
- B. √6
- C. 3
- D. 2
11.计算:25的平方根是 .
12.分式
与
的最简公分母是 .
| 1 |
| x2-2x |
| 1 |
| x |
13.命题“如果a=b,那么a2=b2”的逆命题是 .
14.已知△ABC≌△DEF,若AB=5,BC=6,AC=7,则△DEF的周长是 .
15.
√12
÷√27
×√18
= .16.如图,∠A=∠B=90°,AB=100,E,F分别为线段AB和射线BD上的一点,若点E从点B出发向点A运动,同时点F从点B出发向点D运动,二者速度之比为2:3,运动到某时刻同时停止,在射线AC上取一点G,使△AEG与△BEF全等,则AG的长为 .
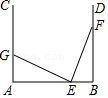

17.计算:
(1)
(2)解方程:
=
.
(1)
√8
+√32
-(√2
-4√
);| 1 |
| 2 |
(2)解方程:
| 3 |
| x+1 |
| 5 |
| x+3 |
18.解不等式组:
,把它的解集在数轴上表示出来,并写出其整数解.
| { |
|
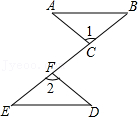
19.如图,点C,F在线段BE上,BF=EC,∠1=∠2,AC=DF.试说明:
(1)△ABC≌△DEF;
(2)AB∥DE.
(1)△ABC≌△DEF;
(2)AB∥DE.

20.先化简,再求值:
-
,其中a=2.
| a2-1 |
| a2-2a+1 |
| a |
| a2-a |
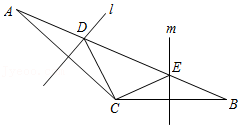
21.如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB于点D和点E.
(1)若AB=10,则△CDE的周长是多少?为什么?
(2)若∠ACB=125°,求∠DCE的度数.
(1)若AB=10,则△CDE的周长是多少?为什么?
(2)若∠ACB=125°,求∠DCE的度数.

22.某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜,某超市看好甲、乙两种有机蔬菜的市场价值,经调查甲种蔬菜进价每千克m元,售价每千克16元;乙种蔬菜进价每千克n元,售价每千克18元.
(1)该超市购进甲种蔬菜15千克和乙种蔬菜20千克需要430元;购进甲种蔬菜10千克和乙种蔬菜8千克需要212元,求m,n的值.
(2)该超市决定每天购进甲、乙两种蔬菜共100千克,且投入资金不少于1160元又不多于1168元,设购买甲种蔬菜x千克(x正整数),求有哪几种购买方案.
(1)该超市购进甲种蔬菜15千克和乙种蔬菜20千克需要430元;购进甲种蔬菜10千克和乙种蔬菜8千克需要212元,求m,n的值.
(2)该超市决定每天购进甲、乙两种蔬菜共100千克,且投入资金不少于1160元又不多于1168元,设购买甲种蔬菜x千克(x正整数),求有哪几种购买方案.
23.阅读并解答问题:
=
=
=
=
=
=2-
⋯⋯
上面的计算过程叫做“分母有理化”,仿照上述计算过程,解答下列问题:
(1)将
的分母有理化;
(2)已知a=
,b=
,求a+b的值;
(3)计算
+
+⋯+
+
.
| 1 |
√2 +1 |
√2 -1 |
| ( √2 +1)(√2 -1) |
√2
-1;| 1 |
√3 +√2 |
√3 -√2 |
| ( √3 +√2 )(√3 -√2 ) |
√3
-√2
;| 1 |
| 2+ √3 |
| 2- √3 |
| (2+ √3 )(2-√3 ) |
√3
;⋯⋯
上面的计算过程叫做“分母有理化”,仿照上述计算过程,解答下列问题:
(1)将
| 1 |
√5 +2 |
(2)已知a=
| 1 |
√7 +√6 |
| 1 |
√7 -√6 |
(3)计算
| 1 |
√2 +1 |
| 1 |
√3 +√2 |
| 1 |
√99 +√98 |
| 1 |
√100 +√99 |
24.已知三角形ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图1,E、F分别是AB、AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)如图2,若E、F分别为AB、CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.

(1)如图1,E、F分别是AB、AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)如图2,若E、F分别为AB、CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.






