试卷题目
1．下列是最简二次根式的是( )
- A. √a2
- B. √8
- C. √
3 2 - D. √14
2．下列计算正确的是( )
- A. √2+√5=√7
- B. 2+√2=2√2
- C. 3√2-√2=3
- D. √2-√=
1 2 √22
3．下列性质，平行四边形具有而一般四边形不具有的是( )
- A. 对角相等
- B. 内角和360°
- C. 外角和360°
- D. 不稳定性
4．正方形的边长为a，其面积与长为8．宽为6的长方形的面积相等，则a的值是( )
- A. 48
- B. 4√3
- C. 24
- D. 2√12
5．我国汉代的赵爽在注释《周髀算经》时给出了勾股定理的无字证明，人们称它为“赵爽弦图”，“赵爽弦图”指的是( )
- A.
- B.
- C.
- D.
6．菱形的面积为12cm2，一条对角线是6cm，那么菱形的另一条对角线长为( )
- A. 3cm
- B. 4cm
- C. 5cm
- D. 6cm
7．如果
√(2a-1)2
=1-2a，那么a的取值范围是( )- A. a＜
1 2 - B. a≥
1 2 - C. a＞
1 2 - D. a≤
1 2
8．如图，在Rt△ABC中，∠ACB=90°，D是AB的中点，若∠A=26°．则∠BDC的度数为( )
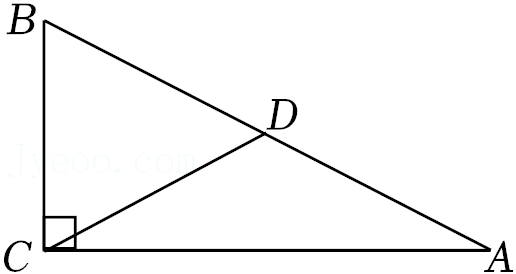
- A. 26°
- B. 52°
- C. 56°
- D. 64°
9．如图，矩形ABCD中，对角线AC，BD交于点O．若∠AOB=60°，BD=2，则BC的长为( )
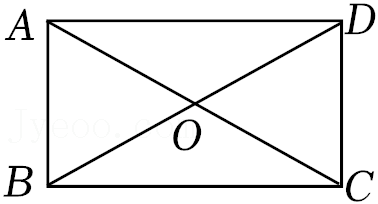
- A. 4
- B. √5
- C. √3
- D. 2
10．将一张平行四边形的纸片折一次，使得折痕平分这个平行四边形的面积．则这样的折纸方法共有( )
- A. 1种
- B. 2种
- C. 4种
- D. 无数种
11．若代数式
√-x+3
有意义，则实数x的取值范围是 ．12．在实数范围内分解因式a2-6= ．
13．(
√50
-√8
)÷√2
= ．14．命题“如果直角三角形的两直角边长分别为a、b，斜边长为c，那么a2+b2=c2”的逆命题是 ．
15．平行四边形的一个内角平分线将对边分成3cm和5cm两个部分，则该平行四边形的周长是 cm．
16．本册课本第十六章的二次根式的学习与整式、分式的学习方法和知识结构存在很多类似和相通的地方，同属于代数式的概念和运算．小华同学学完二次根式后，梳理了本章知识结构简图如下：
你认为空格处应填 ．
你认为空格处应填 ．
17．计算：
(1)(
(2)
(1)(
√
-5| 8 |
| 27 |
√2
)×√6
；(2)
√18
+2√
+(| 1 |
| 2 |
√2
-1)2．18．已知x=
√5
-1，求代数式x2+2x-6的值．19．下面是小东设计的“作矩形”的尺规作图过程．已知：Rt△ABC，∠ABC=90°，
求作：矩形ABCD，
作法：如图，
①作线段AC的垂直平分线交AC于点O；
②连接BO并延长，在延长线上截取OD=OB；
③连接AD，CD．
所以四边形ABCD即为所求作的矩形．
根据小东设计的尺规作图过程．
(1)使用直尺和圆规，补全图形；(保留作图痕迹)
(2)完成下面的证明：
证明：∵OA=OC，OD=OB，
∴四边形ABCD是平行四边形( )．(填推理的依据)
∵∠ABC=90°，
∴平行四边形ABCD是矩形( )．(填推理的依据)
求作：矩形ABCD，
作法：如图，
①作线段AC的垂直平分线交AC于点O；
②连接BO并延长，在延长线上截取OD=OB；
③连接AD，CD．
所以四边形ABCD即为所求作的矩形．
根据小东设计的尺规作图过程．
(1)使用直尺和圆规，补全图形；(保留作图痕迹)
(2)完成下面的证明：
证明：∵OA=OC，OD=OB，
∴四边形ABCD是平行四边形( )．(填推理的依据)
∵∠ABC=90°，
∴平行四边形ABCD是矩形( )．(填推理的依据)
20．如图，在平行四边形ABCD中，DE，BF分别是∠ADC，∠ABC的角平分线．
求证：四边形DEBF是平行四边形．
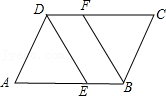
求证：四边形DEBF是平行四边形．
21．如图，将矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上F处，已知CE=3，AB=8，求BF．
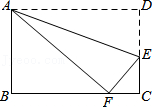
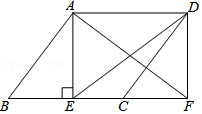
22．如图，在▱ABCD中，AE⊥BC于点E，延长BC至F点使CF=BE，连接AF，DE，DF．
(1)求证：四边形AEFD是矩形；
(2)若AB=6，DE=8，BF=10，求AE的长．
(1)求证：四边形AEFD是矩形；
(2)若AB=6，DE=8，BF=10，求AE的长．
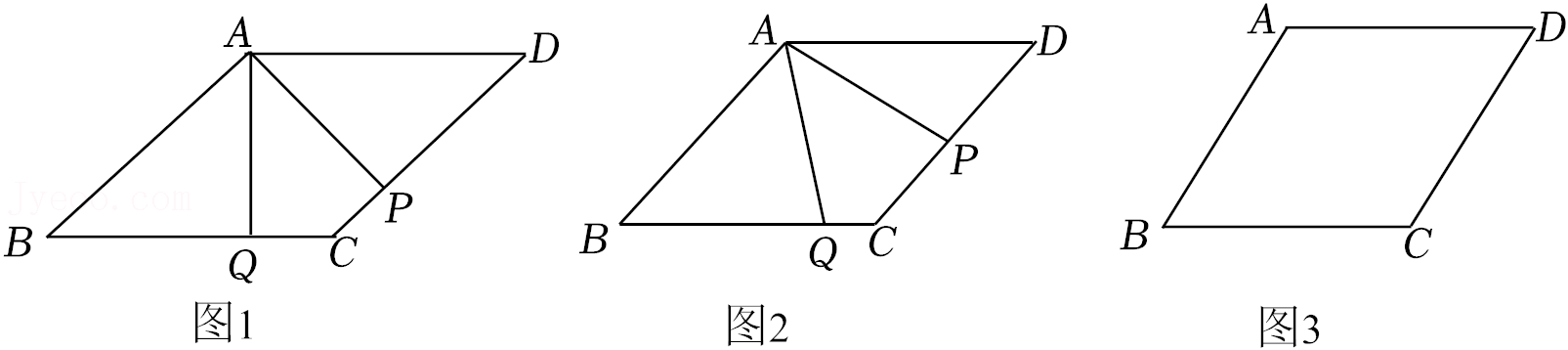
23．已知菱形ABCD中，点P在CD上，连接AP．
(1)在BC上取点Q，使得∠PAQ=∠B，
①图1，当AP⊥CD于点P时，线段AP与AQ之间的数量关系是 ____________．
②如图2，当AP与CD不垂直时，判断①中的结论是否仍然成立，若成立，请给出证明，若不成立，则需说明理由．
(2)在CD的延长线取点N，使得∠PAN=∠B，若AB=4，∠B=60°，∠ANC=45°请依题意画出图形并求此时线段DN的长．
(1)在BC上取点Q，使得∠PAQ=∠B，
①图1，当AP⊥CD于点P时，线段AP与AQ之间的数量关系是 ____________．
②如图2，当AP与CD不垂直时，判断①中的结论是否仍然成立，若成立，请给出证明，若不成立，则需说明理由．
(2)在CD的延长线取点N，使得∠PAN=∠B，若AB=4，∠B=60°，∠ANC=45°请依题意画出图形并求此时线段DN的长．
